【备考2024】高考数学(函数版块)细点逐一突破训练:映射
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知:是集合到集合的函数,如果集合 , 那么集合可能为( )A、 B、{-2} C、 D、{2}2. 已知集合 , , 则下列表达式能建立从集合到集合的函数关系的有( )A、 B、 C、 D、3. 以下给出了4个对应关系: 对应关系 ;
对应关系 中的元素对应它除以4的余数;
你们班的同学 , 身高 , 每个同学的身高;
三角形的周长 , 所有的三角形 , 周长相等的三角形;
其中可称为映射的对应关系共有( )个A、4 B、3 C、2 D、14. 为确保信息安全,信息需加密传输,发送方由明文 密文(加密),接收方由密文 明文(解密),已知加密规则为:明文 对应密文 例如,明文 对应密文 当接收方收到密文 时,则解密得到的明文为( )A、 B、 C、 D、5. 设集合 , ,则下述对应法则 中,不能构成A到B的映射的是( )A、 B、 C、 D、6. 已知集合 到 的映射 ,那么集合 中元素2在 中的象是( )A、5 B、 C、6 D、87. 已知映射 .若集合A中元素x在对应法则f下的像是 ,则B中元素 的原像可以是( )A、 B、 C、 D、28. 设A={x|0≤x≤2},B={y|1≤y≤2},在下列各图中能表示从A到B的映射的是( )A、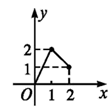 B、
B、 C、
C、 D、
D、 9. 已知映射 ,在映射f下 的原象是( )A、 B、 C、 D、10. 下列在法则 的作用下,从集合 到集合 的对应中,不是映射的个数是( )
9. 已知映射 ,在映射f下 的原象是( )A、 B、 C、 D、10. 下列在法则 的作用下,从集合 到集合 的对应中,不是映射的个数是( )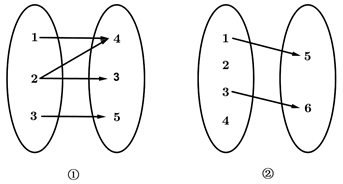
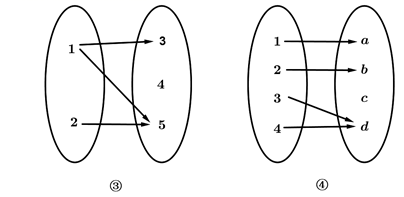 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
11. 设 , , , 从到的映射是“求2倍”则a=12. 下列对应关系中,哪些是从集合A到集合B的映射 .
① ,对应关系:
② ,对应关系
③ {矩形}, {实数},对应关系 矩形的面积
④
⑤ .
13. 设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示从集合M到集合N的函数关系的是.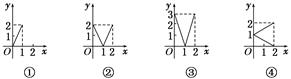 14. 已知 在映射 下的象是 ,则 在 下的象是 , 原象是15. 定义区间 的长度为 ,区间 在映射 所得的对应区间为 ,若区间 的长度比区间 的长度大5,则 .16. 在对应法则 的作用下, 中元素 与 中元素 一一对应,则与 中元素 对应的 中元素是.17. 设f:x→ax-1为从集合A到B的映射,若f(2)=3,则f(3)=.18. 已知集合 是从集合 到集合 的映射: ,则在 的作用下,原像 的像是 , 像 的原像是.19. 函数 的定义域为A,若 时总有 为单函数.例如,函数 =2x+1( )是单函数.下列命题:
14. 已知 在映射 下的象是 ,则 在 下的象是 , 原象是15. 定义区间 的长度为 ,区间 在映射 所得的对应区间为 ,若区间 的长度比区间 的长度大5,则 .16. 在对应法则 的作用下, 中元素 与 中元素 一一对应,则与 中元素 对应的 中元素是.17. 设f:x→ax-1为从集合A到B的映射,若f(2)=3,则f(3)=.18. 已知集合 是从集合 到集合 的映射: ,则在 的作用下,原像 的像是 , 像 的原像是.19. 函数 的定义域为A,若 时总有 为单函数.例如,函数 =2x+1( )是单函数.下列命题:①函数 = (x R)是单函数;②若 为单函数, 且 则 ;③若f:A B为单函数,则对于任意b B,它至多有一个原象;
④函数f(x)在某区间上具有单调性,则f(x)一定是单函数.其中的真命题是.(写出所有真命题的编号)
20. 在映射 中, ,且 ,则 中的元素 在 中对应的元素为 .三、解答题
-
21. 已知集合 ,函数 的定义域为 ,值域为A.(1)、若 ,求不同的函数 的个数;(2)、若 ,
(ⅰ)求不同的函数 的个数;
(ⅱ)若满足 ,求不同的函数 的个数.
22. 设f:A→B是A到B的一个映射,其中 ,f:(x,y)→(x-y,x+y),求与A中的元素(-1,2)相对应的B中的元素和与B中的元素(-1,2)相对应的A中的元素.23. 已知集合A到集合B={0,1, }的映射f:x→ ,那么集合A中的元素最多有几个?并写出元素个数最多时的集合A.24. 设A=B={a,b,c,d,e,…,x,y,z}(元素为26个英文字母),作映射A→B为:并称A中字母拼成的文字为明文,相应B中对应字母拼成的文字为密文,则:
 (1)、“mathematics”的密文是什么?(2)、试破译密文“ju jt gvooz”.25. 已知集合A=R,B={(x,y)|x,y∈R},f:A→B是从集合A到B的映射.若f:x→(x+1,x﹣1),求A中元素3在B中的对应元素和B中元素(﹣4,﹣6)在A中的对应元素.26. 设f:A→B是集合A到集合B的映射,其中A={实数},B=R,f:x→x2﹣2x﹣1,求A中元素1+ 的像和B中元素﹣1的原像.27. 设集合A={a,b,c,d},B={1,2,3,4,5,6},则从集合A到集合B的映射中能构成f(a)≤f(b)≤f(c)≤f(d)的不同映射个数是多少?28. 设f:A→B是从A 到B的一个映射,其中A=B={(x,y)|x,y∈R},(x,y)在映射f的作用下的像是(2x﹣y,2y﹣x),求:(1)、求A中元素(﹣1,2)在f作用下的像(2)、求B中元素(3,﹣3)在f 作用下的原像.
(1)、“mathematics”的密文是什么?(2)、试破译密文“ju jt gvooz”.25. 已知集合A=R,B={(x,y)|x,y∈R},f:A→B是从集合A到B的映射.若f:x→(x+1,x﹣1),求A中元素3在B中的对应元素和B中元素(﹣4,﹣6)在A中的对应元素.26. 设f:A→B是集合A到集合B的映射,其中A={实数},B=R,f:x→x2﹣2x﹣1,求A中元素1+ 的像和B中元素﹣1的原像.27. 设集合A={a,b,c,d},B={1,2,3,4,5,6},则从集合A到集合B的映射中能构成f(a)≤f(b)≤f(c)≤f(d)的不同映射个数是多少?28. 设f:A→B是从A 到B的一个映射,其中A=B={(x,y)|x,y∈R},(x,y)在映射f的作用下的像是(2x﹣y,2y﹣x),求:(1)、求A中元素(﹣1,2)在f作用下的像(2)、求B中元素(3,﹣3)在f 作用下的原像.