【备考2024】高考数学(函数版块)细点逐一突破训练:函数的值域
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知 , 关于该函数有下列四个说法:
①的最小正周期为;
②在上单调递增;
③当时,的取值范围为;
④的图象可由的图象向左平移个单位长度得到.
以上四个说法中,正确的个数为( )
A、1 B、2 C、3 D、42. 下列函数中,值域为 的是( )
A、 B、 C、 D、3. 已知当x∈[0,1]时,函数y=(mx﹣1)2 的图象与y= +m的图象有且只有一个交点,则正实数m的取值范围是( )A、(0,1]∪[2 ,+∞) B、(0,1]∪[3,+∞) C、(0, )∪[2 ,+∞) D、(0, ]∪[3,+∞)4. 已知函数 , 存在实数使得成立,若正整数的最大值为6,则的取值范围为( )A、 B、 C、 D、5. 已知函数 , 则下列说法正确的有( )A、若 , 则 B、将的图象向左平移个单位长度后得到的图象关于轴对称 C、若在上有且仅有4个零点,则的取值范围为 D、是的导函数,令.则在上的值域为6. 已知函数 , 则( )A、有一个零点 B、在上单调递减 C、有两个极值点 D、若 , 则7. 十九世纪德国数学家狄利克雷提出了“狄利克雷函数”它在现代数学的发展过程中有着重要意义,若函数 , 则下列实数不属于函数值域的是( )A、3 B、2 C、1 D、08. 设函数的导函数为 , 若在其定义域内存在 , 使得 , 则称为“有源”函数.已知是“有源”函数,则a的取值范围是( )A、 B、 C、 D、9. 已知线段PQ的中点为等边三角形ABC的顶点A,且 , 当PQ绕点A转动时,的取值范围是( )A、 B、 C、 D、10. 函数 在 上的图象大致为( )A、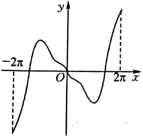 B、
B、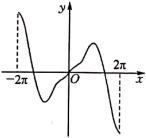 C、
C、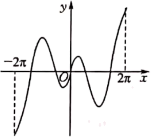 D、
D、 11. 下面关于函数的结论,其中错误的是( )A、的值域是 B、是周期函数 C、的图象关于直线对称 D、当时12. 已知函数为奇函数,且的图象和函数的图象交于不同的两点A,B,若线段的中点在直线上,则的值域为( )A、 B、 C、 D、13. 已知函数 , , , 则下列结论正确的是( )A、在上单调递增 B、当时,方程有且只有3个不同实根 C、的值域为 D、若对于任意的 , 都有成立,则
11. 下面关于函数的结论,其中错误的是( )A、的值域是 B、是周期函数 C、的图象关于直线对称 D、当时12. 已知函数为奇函数,且的图象和函数的图象交于不同的两点A,B,若线段的中点在直线上,则的值域为( )A、 B、 C、 D、13. 已知函数 , , , 则下列结论正确的是( )A、在上单调递增 B、当时,方程有且只有3个不同实根 C、的值域为 D、若对于任意的 , 都有成立,则二、填空题
-
14. 设函数 , 的值域是 , 设 , 若恰有两个零点,则a的取值范围为 .15. 已知在中,角所对边分别为 , 满足 , 且 , 则的取值范围为.16. 函数的值域为.17. 函数f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)+2g(x)=ex , 若对任意x∈(0,2],不等式f(2x)﹣mg(x)≥0成立,则实数m的取值范围是.18. 若函数 ( 且 )的值域是 ,则实数 的取值范围是 .19. 设函数 ,已知 的极大值与极小值之和为 ,则 的值域为 .20. 函数 ( )的值域有6个实数组成,则非零整数 的值是.21. 已知函数 在R上是增函数,且存在垂直于y轴的切线,则 的取值范围是.22. 设函数 的定义域为 ,若对于任意 ,存在 ,使 ( 为常数)成立,则称函数 在 上的“半差值”为 .下列四个函数中,满足所在定义域上“半差值”为 的函数是(填上所有满足条件的函数序号).① ;② ;③ ;④ .23. 若对 ,都有 ,则实数 的取值范围是.
三、解答题
-
24. 在平面直角坐标系xOy中,椭圆E: =1(a>b>0)的离心率为 ,焦距为2.(14分)
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线l:y=k1x﹣ 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2= ,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.
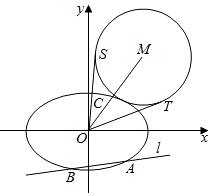 25. 已知函数f(x)=|x+1|﹣|x﹣2|.
25. 已知函数f(x)=|x+1|﹣|x﹣2|.(Ⅰ)求不等式f(x)≥1的解集;
(Ⅱ)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
26. 已知函数.(1)、求函数的最小正周期及对称轴方程(2)、求在上的值域.27. 设是定义域为的函数,当时,.(1)、已知在区间上严格增,且对任意 , 有 , 证明:函数在区间上是严格增函数;(2)、已知 , 且对任意 , 当时,有 , 若当时,函数取得极值,求实数的值;(3)、已知 , 且对任意 , 当时,有 , 证明:.28. 在锐角中,角的对边分别为 , 且 , , 依次组成等差数列.(1)、求的值;(2)、若 , 求的取值范围.29. 已知的三个角 , , 的对边分别为 , , , 且.(1)、求边;(2)、若是锐角三角形,且________,求的面积的取值范围.要求:从① , ②从这两个条件中任选一个,补充在上面的问题中,并给出解答.如果选择多个条件分别解答,按第一个解答计分.
30. 已知函数 .(1)、讨论函数的单调性;(2)、若关于x的方程有两个实数解,求a的最大整数值.31. 在中,的对边分别为.(1)、若 , 求的值;(2)、若的平分线交于点 , 求长度的取值范围.32. 已知半圆的直径 , 点为圆弧上一点(异于点),过点作的垂线,垂足为.(1)、若 , 求的面积;(2)、求的取值范围.