【备考2024】高考数学(函数版块)细点逐一突破训练:函数的定义域及其求法
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 函数 的定义域是( )A、 B、 C、R D、2. 设函数y= 的定义域为A,函数y=ln(1﹣x)的定义域为B,则A∩B=( )A、(1,2) B、(1,2] C、(﹣2,1) D、[﹣2,1)3. 已知集合 , 则( )A、 B、 C、 D、4. 已知 ,则函数 的图象不可能是( )A、
 B、
B、 C、
C、 D、
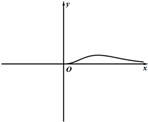
D、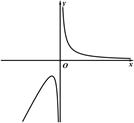 5. 函数的定义域为( )A、 B、 C、 D、6. 若函数的定义域和值域的交集为空集,则正数的取值范围是( )A、 B、 C、 D、7. 已知函数的图象如图所示,则的解析式可能是( )(是自然对数的底数)
5. 函数的定义域为( )A、 B、 C、 D、6. 若函数的定义域和值域的交集为空集,则正数的取值范围是( )A、 B、 C、 D、7. 已知函数的图象如图所示,则的解析式可能是( )(是自然对数的底数) A、 B、 C、 D、8. 已知集合 , , 则( )A、 B、 C、 D、9. 函数的部分图象大致为( )A、
A、 B、 C、 D、8. 已知集合 , , 则( )A、 B、 C、 D、9. 函数的部分图象大致为( )A、 B、
B、 C、
C、 D、
D、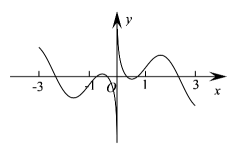 10. 已知函数的部分图像如图所示,则的解析式可能是( )
10. 已知函数的部分图像如图所示,则的解析式可能是( ) A、 B、 C、 D、11. 下列函数中,定义域与值域均为R的是( )A、 B、 C、 D、12. 函数 定义域为( )A、 B、 C、 D、
A、 B、 C、 D、11. 下列函数中,定义域与值域均为R的是( )A、 B、 C、 D、12. 函数 定义域为( )A、 B、 C、 D、二、填空题
-
13. 函数 的定义域是 .14. 函数 的定义域是 .15. 函数 的定义域是.16. 函数的定义域为 .17. 函数的定义域为.18. 函数的定义域是 .19. 函数的定义域是 .20. 函数的定义域为.21. 设函数f(x)= (a<0)的定义域为D,若所有点(s,f(t))(s、t∈D)构成一个正方形区域,则a的值为 .22. 函数的定义域是.23. 函数的定义域为.24. 函数的定义域是.25. 函数的定义域是
三、解答题
-
26. 已知函数 ( 且 )经过定点 ,函数 ( 且 )的图象经过点 .(1)、求函数 的定义域与值域;(2)、若函数 在 上有两个零点,求 的取值范围.27. 设 为实数,函数 .(1)、若 ,求 的定义域;(2)、若 ,且 有两个不同的实数根,求 的取值范围.28. 已知函数 ,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:(1)、 的单调递增区间;(2)、 在区间 的取值范围.
条件①: ;条件②: ;条件③: .
注:如果选择不同条件分别解答,按第一个解答计分.
29. 从秦朝统一全国币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设 ,五个正方形的面积和为S .
 (1)、求面积S关于 的函数表达式,并求定义域;(2)、求面积S的最小值及此时 的值.30. 已知函数 的极大值为 ,其中 为自然对数的底数.(1)、求实数k的值;(2)、若函数 ,对任意 , 恒成立.
(1)、求面积S关于 的函数表达式,并求定义域;(2)、求面积S的最小值及此时 的值.30. 已知函数 的极大值为 ,其中 为自然对数的底数.(1)、求实数k的值;(2)、若函数 ,对任意 , 恒成立.(i)求实数a的取值范围;
(ii)证明: .
31. 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形 对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1 ,且 ,设 ,透光区域的面积为S.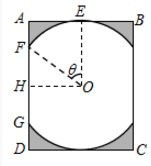 (1)、S关于 的函数关系式,并求出定义域;(2)、根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边AB的长度.32. 已知函数 ,若函数 .(1)、求函数 的定义域;(2)、求函数 的最值.
(1)、S关于 的函数关系式,并求出定义域;(2)、根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边AB的长度.32. 已知函数 ,若函数 .(1)、求函数 的定义域;(2)、求函数 的最值.
