贵州省毕节地区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
1. 下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在中, , , 直线 , 顶点在直线上,直线交于点 , 交于点 , 若 , 则的度数是( )
2. 如图,在中, , , 直线 , 顶点在直线上,直线交于点 , 交于点 , 若 , 则的度数是( ) A、 B、 C、 D、3. 如图,在数轴上点A表示的数是2,点C表示的数是 , , , 以点A为圆心,的长为半径画弧交数轴于点D,则点D表示的数是( )
A、 B、 C、 D、3. 如图,在数轴上点A表示的数是2,点C表示的数是 , , , 以点A为圆心,的长为半径画弧交数轴于点D,则点D表示的数是( ) A、 B、 C、 D、4. 如图,在中, , , 线段的垂直平分线分别交 , 于点 , , 连接若 , 则的长为( )
A、 B、 C、 D、4. 如图,在中, , , 线段的垂直平分线分别交 , 于点 , , 连接若 , 则的长为( )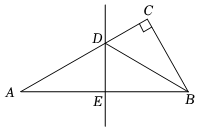 A、 B、 C、 D、5. 若关于x的一元一次方程有整数解,且关于y的不等式组有且只有三个整数解,则满足所有条件的整数m的和是( )A、 B、 C、 D、6. 已知实数 , , 满足 , , 则下列判断正确的是( ).A、 , B、 , C、 , D、 ,7. 在平面直角坐标系中,已知点 , 将线段平移得到线段 , 若点的对应点的坐标是 , 则点的对应点的坐标是( )A、 B、 C、 D、8. 下列分解因式正确的是( )A、 B、 C、 D、9. 下列因式分解正确的是( )A、 B、 C、 D、10. 多项式因式分解的结果是( )A、x(x-4)+4 B、(x+2)(x-2) C、(x+2)2 D、(x-2)211. 为创建文明城市,减少施工对环境造成的影响,某施工队在小区里对一段全长为米的地下管线进行修复时,实际每天的工作效率比原计划提高了 , 结果提前天完成修复任务,求实际每天修复管线多少米?设原计划每天修复管线米,则可列方程为( )A、 B、 C、 D、12. 如图所示,已知 , 正五边形的顶点A、B在射线上,顶点E在射线上,则的度数为( )
A、 B、 C、 D、5. 若关于x的一元一次方程有整数解,且关于y的不等式组有且只有三个整数解,则满足所有条件的整数m的和是( )A、 B、 C、 D、6. 已知实数 , , 满足 , , 则下列判断正确的是( ).A、 , B、 , C、 , D、 ,7. 在平面直角坐标系中,已知点 , 将线段平移得到线段 , 若点的对应点的坐标是 , 则点的对应点的坐标是( )A、 B、 C、 D、8. 下列分解因式正确的是( )A、 B、 C、 D、9. 下列因式分解正确的是( )A、 B、 C、 D、10. 多项式因式分解的结果是( )A、x(x-4)+4 B、(x+2)(x-2) C、(x+2)2 D、(x-2)211. 为创建文明城市,减少施工对环境造成的影响,某施工队在小区里对一段全长为米的地下管线进行修复时,实际每天的工作效率比原计划提高了 , 结果提前天完成修复任务,求实际每天修复管线多少米?设原计划每天修复管线米,则可列方程为( )A、 B、 C、 D、12. 如图所示,已知 , 正五边形的顶点A、B在射线上,顶点E在射线上,则的度数为( )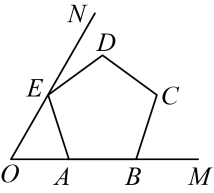 A、 B、 C、 D、13. 如图,在四边形纸片中, , 将纸片折叠,使点C、D落在边上的点处,折痕为 , 则( )
A、 B、 C、 D、13. 如图,在四边形纸片中, , 将纸片折叠,使点C、D落在边上的点处,折痕为 , 则( ) A、 B、 C、 D、14. 闻宏商店计划用不超过元的货款,购进、两种单价分别为元、元的商品共件,据市场行情,销售、商品各一件分别可获利元、元,两种商品均售完若所获利润大于元,则该商店进货方案有( )A、种 B、种 C、种 D、种15. 已知 , 则值为( )A、10 B、11 C、15 D、16
A、 B、 C、 D、14. 闻宏商店计划用不超过元的货款,购进、两种单价分别为元、元的商品共件,据市场行情,销售、商品各一件分别可获利元、元,两种商品均售完若所获利润大于元,则该商店进货方案有( )A、种 B、种 C、种 D、种15. 已知 , 则值为( )A、10 B、11 C、15 D、16二、填空题
-
16. 已知 , 则 .17. 关于x的分式方程的解为正数,且关于y的不等式组的解集为 , 则所有满足条件的整数a的平均数为 .18. 如图,在中, , 将沿着的方向平移至 , 若四边形的面积为24,则平移的距离为 .
 19. 已知x-=3,则= .20. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于 .
19. 已知x-=3,则= .20. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于 .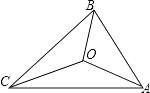
三、解答题
-
21. 因式分解:(1)、;(2)、 .22. 解下列不等式(组):(1)、;(2)、 .23. 其中x、y满足方程组24. 端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,每千克A粽子节前的进价比节后多2元,节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克.根据以上信息,解答下列问题:(1)、该商场节后每千克A粽子的进价是多少元?(2)、如果该商场在节前和节后共购进A粽子400千克,且总费用不超过4600元,并按照节前每千克20元,节后每千克16元全部售出,那么该商场节前购进多少千克A粽子获得利润最大?最大利润是多少?25. 如图,已知的对角线 , 交于点O,过点O且与 , 分别相交于点E、F.
 (1)、求证:;(2)、若 , , , 求的长.26. 阅读材料:利用公式法,可以将一些形如的多项式变形为的形式,我们把这样的变形方法叫做多项式的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解.例如
(1)、求证:;(2)、若 , , , 求的长.26. 阅读材料:利用公式法,可以将一些形如的多项式变形为的形式,我们把这样的变形方法叫做多项式的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解.例如根据以上材料,解答下列问题.
(1)、分解因式:;(2)、求多项式的最小值27. 如图1,直线 , 直线与 , 分别交于点G,H, . 将一个直角三角板按如图1所示放置,使点N,M分别在直线 , 上,且在点G,H的右侧,已知 .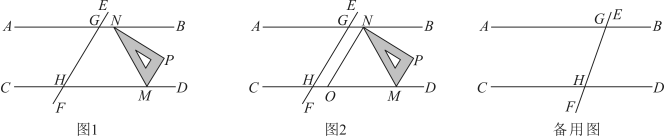 (1)、若 , 则的度数为;(2)、若 , 对说明理由;(3)、如图2,已知的平分线交直线于点O.
(1)、若 , 则的度数为;(2)、若 , 对说明理由;(3)、如图2,已知的平分线交直线于点O.①当 , 时,求的值;
②现将三角板保持 , 并沿直线向左平移,在平移的过程中,直接写出的度数(用含的代数式表示).