【备考2024】高考数学(函数版块)细点逐一突破训练:奇偶函数图象的对称性
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知函数 及其导函数 的定义域均为R,记 若 均为偶函数,则( )A、 B、 C、 D、2. 设函数 ,则下列函数中为奇函数的是( )A、 B、 C、 D、3. 函数 的图像大致为( )A、
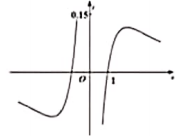 B、
B、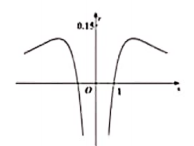 C、
C、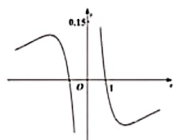 D、
D、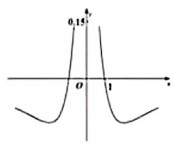 4. 函数f(x)= 的图象大致是( )A、
4. 函数f(x)= 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 5. 函数y= sin2x的图象可能是( )
5. 函数y= sin2x的图象可能是( )
A、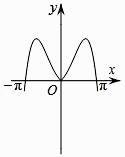 B、
B、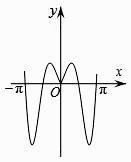 C、
C、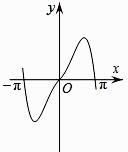 D、
D、 6. 已知函数是定义在上的奇函数, , 当时, , 则( )A、 B、 C、2 D、37. 已知函数 , 其中是其图象上四个不重合的点,直线为函数在点处的切线,则( )A、函数的图象关于中心对称 B、函数的极大值有可能小于零 C、对任意的 , 直线的斜率恒大于直线的斜率 D、若三点共线,则.8. 已知函数与及其导函数与的定义域均为 , 是偶函数,的图象关于点对称,则( )A、 B、 C、 D、9. 函数的定义域均为 , 且 , 关于对称, , 则的值为( )A、-24 B、-32 C、-34 D、-4010. 已知函数是定义在上的奇函数,且的一个周期为2,则( )A、1为的周期 B、的图象关于点对称 C、 D、的图象关于直线对称11. 已知函数 , 的定义域均为 , 为偶函数且 , , 则 ( )A、21 B、22 C、 D、12. 已知函数和及其导函数和的定义域均为 , 若 , , 且为偶函数,则( )A、 B、函数的图象关于直线对称 C、函数的图象关于直线对称 D、13. 已知 , 分别是定义在R上的函数 , 的导函数, , , 且是奇函数,则( )A、的图象关于直线对称 B、的图象关于点对称 C、 D、14. 已知函数 . 若为偶函数.的图象与x轴交点的横坐标构成一个公差为的等差数列.将函数图象上每一点的横坐标缩短为原来的 , 纵坐标不变,再向左平移个单位后得到函数的图象,则( )A、0 B、-2 C、1 D、-115. 已知函数对 , 都有 , 为奇函数,且时, , 下列结论正确的是( )A、函数的图像关于点中心对称 B、是周期为2的函数 C、 D、
6. 已知函数是定义在上的奇函数, , 当时, , 则( )A、 B、 C、2 D、37. 已知函数 , 其中是其图象上四个不重合的点,直线为函数在点处的切线,则( )A、函数的图象关于中心对称 B、函数的极大值有可能小于零 C、对任意的 , 直线的斜率恒大于直线的斜率 D、若三点共线,则.8. 已知函数与及其导函数与的定义域均为 , 是偶函数,的图象关于点对称,则( )A、 B、 C、 D、9. 函数的定义域均为 , 且 , 关于对称, , 则的值为( )A、-24 B、-32 C、-34 D、-4010. 已知函数是定义在上的奇函数,且的一个周期为2,则( )A、1为的周期 B、的图象关于点对称 C、 D、的图象关于直线对称11. 已知函数 , 的定义域均为 , 为偶函数且 , , 则 ( )A、21 B、22 C、 D、12. 已知函数和及其导函数和的定义域均为 , 若 , , 且为偶函数,则( )A、 B、函数的图象关于直线对称 C、函数的图象关于直线对称 D、13. 已知 , 分别是定义在R上的函数 , 的导函数, , , 且是奇函数,则( )A、的图象关于直线对称 B、的图象关于点对称 C、 D、14. 已知函数 . 若为偶函数.的图象与x轴交点的横坐标构成一个公差为的等差数列.将函数图象上每一点的横坐标缩短为原来的 , 纵坐标不变,再向左平移个单位后得到函数的图象,则( )A、0 B、-2 C、1 D、-115. 已知函数对 , 都有 , 为奇函数,且时, , 下列结论正确的是( )A、函数的图像关于点中心对称 B、是周期为2的函数 C、 D、二、填空题
-
16. 黎曼函数是一个特殊的函数,由德因数学家波恩哈德·黎曼发现并提出,在高等数学中有着广泛的应用.黎曼函数定义在上,其解析式如下: , 定义在实数集上的函数满足 , 且函数的图象关于直线对称, , 当时, , 则.17. 写出一个同时满足下列三个条件的函数的解析式.
①;②;③在上单调递增.
18. 已知定义在上的函数满足 , 且当时, , 若的值域为 , 则实数的取值范围为 .19. 已知函数 , 下面四个结论:①的图象是轴对称图形;②的图象是中心对称图形;③在上单调;④的最大值为 . 其中正确的有 .20. 函数的对称轴方程为.21. 设函数 , , , 取 , , , , 则 , , 的大小关系为.(用“<”连接)22. 已知定义在R上的奇函数 满足 ,且在区间 上是增函数,若方程 在区间 上有四个不同的根,则 .23. 已知定义在R上的奇函数 满足 ,当 时, ,则方程 在区间 上所有的实数解之和为 .24. 已知定义在 上的偶函数 满足 .且当 时, .若对于任意 ,都有 ,则实数 的取值范围为 .25. 设函数 满足 ,且当 时 ,又函数 ,则函数 在 上的零点个数为.三、解答题
-
26. 已知在锐角 中,角A,B,C的对边分别为 , , ,且 .
(Ⅰ)求角A的大小;
(Ⅱ)已知函数 ,且方程 有解,求实数t的取值范围.
27. 乐音中包含着正弦函数,平时我们听到的乐音是许多个音的结合,称为复合音,复合音的产生是因为发声体在全段震动,产生基音的同时,其余各部分,如二分之一部分也在震动.某乐音的函数是 , 该函数我们可以看作是函数与相加,利用这两个函数的性质,我们可以探究的函数性质. (1)、求出的最小正周期并写出的所有对称中心;(2)、求使成立的x的取值集合;(3)、判断 , 函数零点的个数,并说明理由.28. 我们知道,函数的图像关于坐标原点成中心对称图形的充要条件是函数为奇函数,有同学发现可以将其推广为:函数的图像关于点成中心对称图形的充要条件是函数为奇函数,(1)、求函数的对称中心;(2)、已知 , , 若对任意的 , 总存在 , 使成立,求实数的取值范围.29. 已知函数( , )的图象关于原点对称.(1)、求实数 , 的值;(2)、①判断在区间上的单调性(只写出结论即可);
(1)、求出的最小正周期并写出的所有对称中心;(2)、求使成立的x的取值集合;(3)、判断 , 函数零点的个数,并说明理由.28. 我们知道,函数的图像关于坐标原点成中心对称图形的充要条件是函数为奇函数,有同学发现可以将其推广为:函数的图像关于点成中心对称图形的充要条件是函数为奇函数,(1)、求函数的对称中心;(2)、已知 , , 若对任意的 , 总存在 , 使成立,求实数的取值范围.29. 已知函数( , )的图象关于原点对称.(1)、求实数 , 的值;(2)、①判断在区间上的单调性(只写出结论即可);②若关于的方程在区间上有两个不同的解,求实数的取值范围.
30. 已知函数 (其中 且 )的图象关于原点对称.(1)、求 , 的值(2)、当 时,关于 的方程 在区间 上有两个不同的解,求实数 的取值范围.31. 如果函数 满足:对定义域内的所有 ,存在常数 , ,都有 ,那么称 是“中心对称函数”,对称中心是点 .(1)、证明点 是函数 的对称中心;(2)、已知函数 ( 且 , )的对称中心是点 .①求实数 的值;
②若存在 ,使得 在 上的值域为 ,求实数 的取值范围.
32. 已知函数 是定义在 上的偶函数,且 ,当 时, .(1)、求函数 的解析式;(2)、解不等式 .
