【备考2024】高考数学(函数版块)细点逐一突破训练:函数奇偶性的判定1
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知是偶函数,则( )A、 B、 C、1 D、22. 函数的大致图象是( ).A、
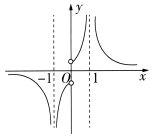 B、
B、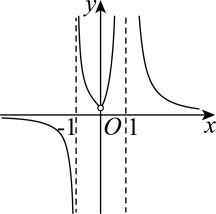 C、
C、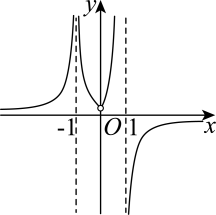 D、
D、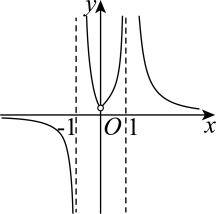 3. 已知定义在上的偶函数 , 其导函数为 , 若 , , 则不等式的解集是( )A、 B、 C、 D、4. 若函数为函数的导函数,且对于任意实数 , 均有 , 且 , 则( )A、函数不可能为奇函数 B、存在实数M,使得 C、存在实数N,使得 D、函数不存在零点5. 函数的部分图像大致为( )A、
3. 已知定义在上的偶函数 , 其导函数为 , 若 , , 则不等式的解集是( )A、 B、 C、 D、4. 若函数为函数的导函数,且对于任意实数 , 均有 , 且 , 则( )A、函数不可能为奇函数 B、存在实数M,使得 C、存在实数N,使得 D、函数不存在零点5. 函数的部分图像大致为( )A、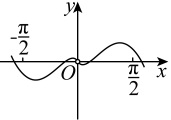 B、
B、 C、
C、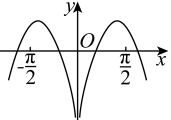 D、
D、 6. 已知函数 , 则( )A、为奇函数 B、为偶函数 C、为奇函数 D、为偶函数7. 函数的图象大致为( )A、
6. 已知函数 , 则( )A、为奇函数 B、为偶函数 C、为奇函数 D、为偶函数7. 函数的图象大致为( )A、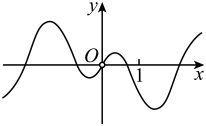 B、
B、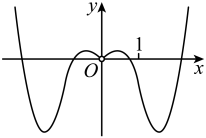 C、
C、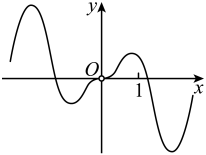 D、
D、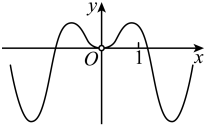 8. 已知函数的定义域是( , ),值域为 , 则满足条件的整数对可以是( )A、 B、 C、 D、9. 定义在上的函数满足 , 且为奇函数,则( )A、-2023 B、-2022 C、2022 D、202310. 已知定义在上且不恒为的函数 , 若对任意的 , 都有 , 则( )A、函数是奇函数 B、对 , 有 C、若 , 则 D、若 , 则11. 设函数的定义域为 , 其导函数为 , 若 , 则下列结论不一定正确的是( )A、 B、 C、 D、12. 函数的图象大致为( )A、
8. 已知函数的定义域是( , ),值域为 , 则满足条件的整数对可以是( )A、 B、 C、 D、9. 定义在上的函数满足 , 且为奇函数,则( )A、-2023 B、-2022 C、2022 D、202310. 已知定义在上且不恒为的函数 , 若对任意的 , 都有 , 则( )A、函数是奇函数 B、对 , 有 C、若 , 则 D、若 , 则11. 设函数的定义域为 , 其导函数为 , 若 , 则下列结论不一定正确的是( )A、 B、 C、 D、12. 函数的图象大致为( )A、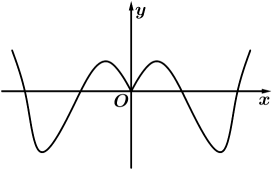 B、
B、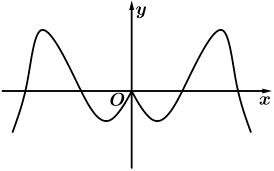 C、
C、 D、
D、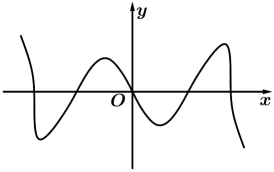 13. 函数的部分图象大致是( )A、
13. 函数的部分图象大致是( )A、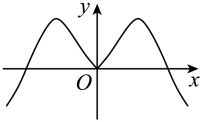 B、
B、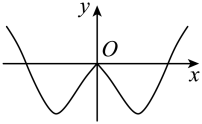 C、
C、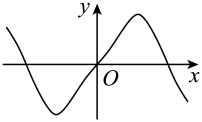 D、
D、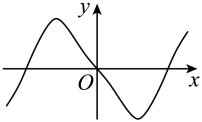 14. 已知定义在上的函数满足 , , 则下列说法正确的是( )A、的周期为2 B、为偶函数 C、 D、15. 在下列函数中,为偶函数的是( )A、 B、 C、 D、
14. 已知定义在上的函数满足 , , 则下列说法正确的是( )A、的周期为2 B、为偶函数 C、 D、15. 在下列函数中,为偶函数的是( )A、 B、 C、 D、二、填空题
-
16. 若定义在上的函数满足: , , 且 , 则满足上述条件的函数可以为.(写出一个即可)17. 若函数为奇函数,则实数a的值为 .18. 已知为定义在上的奇函数,是的导函数, , , 则以下命题:①是偶函数;②;③的图象的一条对称轴是;④ , 其中正确的序号是 .19. 已知函数 , 数列是公差为2的等差数列,若 , 则数列的前n项和 .20. 能说明“存在 , 使得 , f(x)不是偶函数”为真命题的一个函数为.21. 已知函数 , 若函数 , 则函数的图象的对称中心为;若数列为等差数列, , .22. 已知函数 ,若 ,则实数 的取值范围是 .23. 写出一个满足 的奇函数 .24. 已知函数 ,现有以下命题:
① 是偶函数; ② 是以 为周期的周期函数;
③ 的图像关于 对称; ④ 的最大值为 .
其中真命题有 .
25. 已知函数 是定义在 上的奇函数,当 时, ,且曲线 在点 处的切线斜率为4,则 .三、解答题
-
26. 已知(1)、讨论 在 上的单调性;(2)、设 ,试判断 在R上的零点个数,并说明理由.27. 设函数 ,(1)、讨论函数 的奇偶性,并说明理由;(2)、设 ,解关于 的不等式 .28. 设 ,其中常数 .(1)、设 , ,求函数 ( )的反函数;(2)、求证:当且仅当 时,函数 为奇函数.29. 已知函数 .(1)、判断 在其定义域上的单调性,并用函数单调性的定义加以证明;(2)、讨论函数 的奇偶性,并说明理由.30. 已知函数 其中 为实常数.(1)、若 ,解关于 的方程 ;(2)、判断函数 的奇偶性,并说明理由.31. 已知函数f(x)=logax(a>0,且a≠1),且f(2)=1(1)、求a的值,并写出函数f(x)的定义域;(2)、设g(x)=f(2-x)-f(2+x),判断g(x)的奇偶性,并说明理由:(3)、若不等式f(t·9x)≥f(3x-t)对任意x∈[1,2]恒成立,求实数t的取值范围。32. 设 (a,b为实常数).(1)、当a=b=1时,证明:f(x)不是奇函数;(2)、设f(x)是奇函数,求a与b的值;(3)、当f(x)是奇函数时,研究是否存在这样的实数集的子集D,对任何属于D的x、c,都有f(x)<c2﹣3c+3成立?若存在试找出所有这样的D;若不存在,请说明理由.