【备考2024】高考数学(函数版块)细点逐一突破训练:奇函数
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 函数的图象如下图所示,则的解析式可能为( )
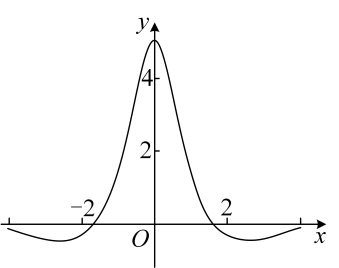 A、 B、 C、 D、2. 已知函数 的定义域为 , 为偶函数, 为奇函数,则( )A、 B、 C、 D、3. 设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若 ( )A、 B、 C、 D、4. 已知函数 , 则( )A、是奇函数 B、的单调递增区间为和 C、的最大值为 D、的极值点为5. 已知是定义在上的奇函数,当时, , 则( )A、-1 B、0 C、1 D、26. 若将函数的图象向右平移个单位后,所得图象对应的函数为奇函数,则的最小值是( )A、 B、 C、 D、7. 设 是定义在R上的奇函数,且当 时, ,则 的解集为( )A、 B、 C、 D、8. 对任意的 , 函数满足 . 若函数在区间上既有最大值又有最小值,则函数的最大值与最小值之和为( )A、0 B、2 C、4 D、89. 已知函数 , 若 , 则x的取值范围是( )A、 B、 C、 D、10. 若函数()是周期为2的奇函数.则下列选项一定正确的是( )A、函数的图象关于点对称 B、2是函数的一个周期 C、 D、11. 已知定义在上的奇函数恒有 , 当时, , 已知 , 则函数在上的零点个数为( )A、4个 B、5个 C、3个或4个 D、4个或5个12. 若是定义在上的奇函数,且 , 则的值为( )A、1 B、2 C、0 D、-113. 已知是定义在R上的奇函数,且当时, , 则( )A、﹣2 B、2 C、﹣6 D、6
A、 B、 C、 D、2. 已知函数 的定义域为 , 为偶函数, 为奇函数,则( )A、 B、 C、 D、3. 设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若 ( )A、 B、 C、 D、4. 已知函数 , 则( )A、是奇函数 B、的单调递增区间为和 C、的最大值为 D、的极值点为5. 已知是定义在上的奇函数,当时, , 则( )A、-1 B、0 C、1 D、26. 若将函数的图象向右平移个单位后,所得图象对应的函数为奇函数,则的最小值是( )A、 B、 C、 D、7. 设 是定义在R上的奇函数,且当 时, ,则 的解集为( )A、 B、 C、 D、8. 对任意的 , 函数满足 . 若函数在区间上既有最大值又有最小值,则函数的最大值与最小值之和为( )A、0 B、2 C、4 D、89. 已知函数 , 若 , 则x的取值范围是( )A、 B、 C、 D、10. 若函数()是周期为2的奇函数.则下列选项一定正确的是( )A、函数的图象关于点对称 B、2是函数的一个周期 C、 D、11. 已知定义在上的奇函数恒有 , 当时, , 已知 , 则函数在上的零点个数为( )A、4个 B、5个 C、3个或4个 D、4个或5个12. 若是定义在上的奇函数,且 , 则的值为( )A、1 B、2 C、0 D、-113. 已知是定义在R上的奇函数,且当时, , 则( )A、﹣2 B、2 C、﹣6 D、6二、填空题
-
14. 已知函数(其中是自然对数的底数,)是奇函数,则实数的值为.15. 已知函数是定义在上的奇函数,且满足 , ,则.16. 已知函数为上的奇函数;且 , 当时, , 则 .17. 若奇函数 , 则 .18. 定义在 上的奇函数 满足 , 且当 时, .则函数 的所有零点之和为.19. 已知为R上的奇函数,且 , 当时, , 则的值为 .20. 已知是奇函数,且当时, . 若 , 则 .21. 已知是定义域为的奇函数,且对任意的满足 , 若时,有 , 则.22. 已知 为奇函数,当 时 则曲线 在 处的切线方程是.23. 已知函数 是定义在R上的奇函数,当 时, ;当 时, ,则 .
三、解答题
-
24. 函数(1)、当是,是否存在实数 , 使得为奇函数;(2)、函数的图像过点 , 且的图像与轴负半轴有两个交点,求实数的取值范围.25. 已知 是定义域为R的奇函数,满足 .(1)、证明: ;(2)、若 ,求式子 的值.26. 已知定义域为 的函数 是奇函数.(1)、求 , 的值;(2)、在(1)的条件下,解不等式 .27. 若函数 为奇函数,且 时 有极小值 .(1)、求实数 的值;(2)、求实数 的取值范围;(3)、若 恒成立,求实数 的取值范围.28. 已知函数是奇函数.(1)、求的值,并求的定义域;(2)、已知实数满足 , 求t的取值范围.29. 已知是定义在上的奇函数,且当时,.(1)、求函数的解析式;(2)、当时,方程有解,求实数的取值范围.30. 已知且 , 函数在R上是单调减函数,且满足下列三个条件中的两个.
①函数为奇函数;②;③.
(1)、从中选择的两个条件的序号为 , 依所选择的条件求得 , ;(2)、利用单调性定义证明函数在上单调递减;(3)、在(1)的情况下,若方程在上有且只有一个实根,求实数的取值范围.31. 已知定义在上的奇函数 . 在时, .(1)、试求的表达式;(2)、若对于上的每一个值,不等式恒成立,求实数的取值范围.32. 设函数是定义在R上的奇函数.(1)、求实数m的值;(2)、若f,且在上的最小值为2,求实数k的取值范围.