【备考2024】高考数学(函数版块)细点逐一突破训练:奇函数与偶函数的性质2
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 设函数f(x)的定义域为R , f(x+1)为奇函数,f(x+2)为偶函数,当 时, .若 ,则 ( )A、 B、 C、 D、2. 设函数f(x)= ,则下列函数中为奇函数的是( )A、f(x-1)-1 B、f(x-1)+1 C、f(x+1)-1 D、f(x+1)+13. 函数 的图象大致为( )A、
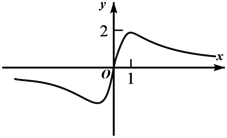 B、
B、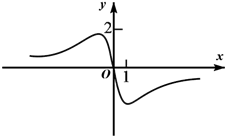 C、
C、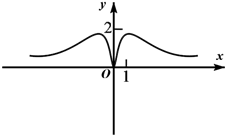 D、
D、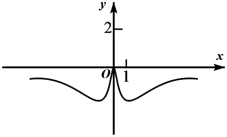 4. 设定义在R上的可导函数与 导函数分别为和 , 若 , 与均为偶函数,则( )A、 B、 C、 D、5. 若函数的图象关于原点对称,且 , 则( )A、-1 B、0 C、1 D、26. 已知定义在上的函数满足 , 且为偶函数,则下列说法一定正确的是( )A、函数的周期为2 B、函数的图象关于对称 C、函数为偶函数 D、函数的图象关于对称7. 设函数的定义域为 , 为奇函数,为偶函数,当时, . 若 , 则( )A、 B、 C、 D、8. 已知与都是定义在上的函数,是奇函数,是偶函数,且 , 都不是常数函数,现有下列三个结论:①;②的图象关于直线对称;③与在上的单调性可能相同 其中正确结论的个数为( )A、0 B、1 C、2 D、39. 已知函数为偶函数,则( )A、-1 B、-2 C、2 D、110. 若奇函数满足 , 且当时, , 则( )A、-1 B、 C、0 D、11. 已知函数的定义域为R,且为偶函数,则( )A、 B、为偶函数 C、 D、12. 已知函数 , 的定义域均为 , 且 , , 若的图象关于直线对称, , 则( )A、-3 B、-1 C、0 D、213. 已知为奇函数,且时, , 则( )A、 B、 C、 D、
4. 设定义在R上的可导函数与 导函数分别为和 , 若 , 与均为偶函数,则( )A、 B、 C、 D、5. 若函数的图象关于原点对称,且 , 则( )A、-1 B、0 C、1 D、26. 已知定义在上的函数满足 , 且为偶函数,则下列说法一定正确的是( )A、函数的周期为2 B、函数的图象关于对称 C、函数为偶函数 D、函数的图象关于对称7. 设函数的定义域为 , 为奇函数,为偶函数,当时, . 若 , 则( )A、 B、 C、 D、8. 已知与都是定义在上的函数,是奇函数,是偶函数,且 , 都不是常数函数,现有下列三个结论:①;②的图象关于直线对称;③与在上的单调性可能相同 其中正确结论的个数为( )A、0 B、1 C、2 D、39. 已知函数为偶函数,则( )A、-1 B、-2 C、2 D、110. 若奇函数满足 , 且当时, , 则( )A、-1 B、 C、0 D、11. 已知函数的定义域为R,且为偶函数,则( )A、 B、为偶函数 C、 D、12. 已知函数 , 的定义域均为 , 且 , , 若的图象关于直线对称, , 则( )A、-3 B、-1 C、0 D、213. 已知为奇函数,且时, , 则( )A、 B、 C、 D、二、填空题
-
14. 已知函数f(x)= 是偶函数,则a=15. 已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是.16. 将函数的图象向左平移个单位长度.得到函数g(x)的图象,若g(x)是奇函数,则φ= .17. 定义在上的函数 , 满足为偶函数,为奇函数,若 , 则.18. 已知 是定义为R的奇函数,当 , ,则 .19. 已知函数 是偶函数,则 .20. 若为奇函数,则的表达式可以为.21. 已知函数为偶函数,当时, , 则的值为 .22. 已知函数为奇函数,当时, , 若 , 则.23. 设为奇函数,且时, , 则.24. 写出一个图象关于直线对称的奇函数 .25. 黎曼函数是一个特殊的函数,由德国数学家波恩哈德·黎曼发现并提出,在高等数学中有着广泛的应用.黎曼函数定义在上,其解析式如下:若函数是定义在R上的奇函数,且对任意x都有 , 当时, , 则.
三、解答题
-
26. 设函数 为定义在(﹣∞,0)∪(0,+∞)上的奇函数.(1)、求实数a的值;(2)、判断函数f(x)在区间(a+1,+∞)上的单调性,并用定义法证明.27. 已知函数.(1)、若 , 求的值;(2)、已知函数的图象经过 ,
(i)若 , 求的值;
(ii)若的三个零点为 , 且 , 求的值.
28. 已知函数 , 是奇函数.(1)、求实数的值;(2)、讨论函数在上的单调性,并求函数在上的最大值和最小值.29. 设函数(且, , ),若是定义在上的奇函数且.(1)、求k和a的值;(2)、判断其单调性(无需证明),并求关于t的不等式成立时,实数t的取值范围;(3)、函数 , , 求的值域.30. 已知函数为奇函数,其中且.(1)、求实数a的值,判断并证明函数的单调性;(2)、函数在区间上的值域是 , 求k的取值范围.31. 已知函数(1)、若是奇函数,求的值;(2)、若在上恒成立,求的取值范围.32. 已知是定义在上的偶函数,当时且单调递增.(1)、求函数在上的解析式;(2)、若 , 求实数a的取值范围.33. 已知是定义在上的奇函数,其中、 , 且.(1)、求、的值;(2)、判断在上的单调性,并用单调性的定义证明;(3)、设 , 若对任意的 , 总存在 , 使得成立,求非负实数的取值范围.