【备考2024】高考数学(函数版块)细点逐一突破训练:奇函数与偶函数的性质1
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知函数 . 记 , 则( )A、 B、 C、 D、2. 函数 在区间 的图像大致为( )A、
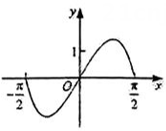 B、
B、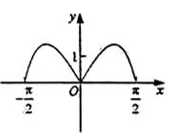 C、
C、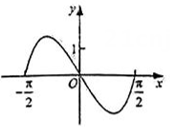 D、
D、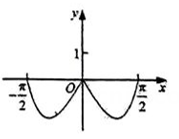 3. 已知函数 及其导函数 的定义域均为R,记 若 均为偶函数,则( )A、 B、 C、 D、4. 设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若 ( )A、 B、 C、 D、5. 已知函数满足 , 且是偶函数,当时, , 则( )A、 B、3 C、 D、6. 定义在上的连续可导函数的导函数为 , 满足 , 且为奇函数.当时, , 则( )A、-5 B、-2 C、-1 D、17. 函数的图像大致为( )A、
3. 已知函数 及其导函数 的定义域均为R,记 若 均为偶函数,则( )A、 B、 C、 D、4. 设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若 ( )A、 B、 C、 D、5. 已知函数满足 , 且是偶函数,当时, , 则( )A、 B、3 C、 D、6. 定义在上的连续可导函数的导函数为 , 满足 , 且为奇函数.当时, , 则( )A、-5 B、-2 C、-1 D、17. 函数的图像大致为( )A、 B、
B、 C、
C、 D、
D、 8. 函数的图象可能为( )A、
8. 函数的图象可能为( )A、 B、
B、 C、
C、 D、
D、 9. 设函数在R上存在导数 , 对任意的 , 有 , 且在上 . 若 , 则实数a的取值范围为( )A、 B、 C、 D、10. 已知函数()是奇函数,且 , 是的导函数,则( )A、 B、的周期是4 C、是偶函数 D、11. 函数的部分图像大致形状是( )A、
9. 设函数在R上存在导数 , 对任意的 , 有 , 且在上 . 若 , 则实数a的取值范围为( )A、 B、 C、 D、10. 已知函数()是奇函数,且 , 是的导函数,则( )A、 B、的周期是4 C、是偶函数 D、11. 函数的部分图像大致形状是( )A、 B、
B、 C、
C、 D、
D、 12. 已知函数是奇函数,且 , 若是函数的一个零点,则( )A、-4 B、0 C、2 D、413. 已知函数及其导函数的定义域均为 , 记 . 若为奇函数,为偶函数,且 , , 则( )A、670 B、672 C、674 D、67614. 若 , , 分别是定义在R上的偶函数、奇函数、偶函数,则下列函数不是偶函数的是( )A、 B、 C、 D、
12. 已知函数是奇函数,且 , 若是函数的一个零点,则( )A、-4 B、0 C、2 D、413. 已知函数及其导函数的定义域均为 , 记 . 若为奇函数,为偶函数,且 , , 则( )A、670 B、672 C、674 D、67614. 若 , , 分别是定义在R上的偶函数、奇函数、偶函数,则下列函数不是偶函数的是( )A、 B、 C、 D、二、填空题
-
15. 若 是奇函数,则 , .16. 若函数 为偶函数, 且当 时, , 则 .17. 已知函数为偶函数,且 , 则.18. 已知函数是定义在上的奇函数,且当时, . 若 , 则实数a的值为 .19. 已知是定义域为的奇函数,当时, , 则.20. 对于定义在上的奇函数 , 当时, , 则该函数的值域为.21. 若函数是偶函数,则 .22. 若函数为奇函数,则.23. 若为奇函数,则实数.24. 已知函数是定义在上的奇函数,且 , 则.25. 定义在上的奇函数满足 , 当时, , 则.
三、解答题
-
26. 已知函数是偶函数.(1)、求实数的值;(2)、设 , 若函数与的图象有且仅有一个公共点, 求实数的取值范围.27. 设函数 , .(1)、若 , , 函数是偶函数,求方程的解集;(2)、求函数的值域.28. 已知函数 满足 .(1)、试问是否存在 ,使得函数 为奇函数?若存在,求 的值;若不存在,请说明理由.(2)、若 , , ,求 的取值范围.29. 已知函数 .(a为实常数)(1)、讨论函数 的奇偶性,并说明理由;(2)、当 为奇函数时,对任意 ,不等式 恒成立,求实数u的最大值.30. 设函数 , 为常数.(1)、若 为偶函数,求 的值;(2)、设 , , 为减函数,求实数 的取值范围.31. 已知函数 .(1)、设 ,判断函数 的奇偶性,并说明理由;(2)、设函数 ,对任意 ,求 在区间 上零点个数的所有可能值。32. 已知 ,函数 .(1)、求 的值,使得 为奇函数;(2)、若 且 对任意 都成立,求 的取值范围.