【备考2024】高考数学(函数版块)细点逐一突破训练:函数的最值及其几何意义
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知单位向量 不共线,且向量 满足 若 对任意实数λ都成立,则向量 夹角的最大值是()A、 B、 C、 D、2. 下列函数中最小值为4的是( )A、 B、 C、 D、3. 已知函数 , 且 , , 则下列结论正确的是( )A、 B、 C、在上单调递减 D、最小值为4. 设关于 、 的表达式 , 当 、 取遍所有实数时, ( )A、既有最大值, 也有最小值 B、有最大值,无最小值 C、无最大值,有最小值 D、既无最大值, 也无最小值5. 若函数的定义域为 , 如果对中的任意一个 , 都有 , 且 , 则称函数为“类奇函数”.若某函数是“类奇函数”,则下列命题中,错误的是( )A、若0在定义域中,则 B、若 , 则 C、若在上单调递增,则在上单调递减 D、若定义域为 , 且函数也是定义域为的“类奇函数”,则函数也是“类奇函数”6. “家在花园里,城在山水间.半城山色半城湖,美丽惠州和谐家园......”首婉转动听的《美丽惠州》唱出了惠州的山姿水色和秀美可人的城市环境.下图1是惠州市风景优美的金山湖片区地图,其形状如一颗爱心.图2是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )
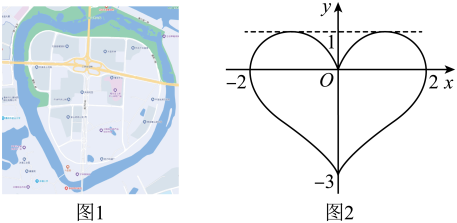 A、 B、 C、 D、7. 已知函数是的导函数,则( )A、与的周期相同 B、与的值域相同 C、可能是奇函数 D、的最大值是8. 若函数的最小值为m,则函数的最小值为( )A、 B、 C、 D、9. 已知函数 , 下列关于该函数的结论正确的是( )A、的图象关于直线对称 B、的一个周期是 C、在区间上单调递增 D、的最大值为10. 已知函数 , 则( )A、的定义域是 B、有最大值 C、不等式的解集是 D、在上单调递增11. 已知是函数的零点,则下列说法正确的是( )A、 B、 C、 D、12. 平面内到两定点距离之积为常数的点的轨迹称为卡西尼卵形线,它是1675年卡西尼在研究土星及其卫星的运行规律时发现的,已知在平面直角坐标系中, , , 动点P满足 , 则下列结论正确的是( )A、点的横坐标的取值范围是 B、的取值范围是 C、面积的最大值为 D、的取值范围是
A、 B、 C、 D、7. 已知函数是的导函数,则( )A、与的周期相同 B、与的值域相同 C、可能是奇函数 D、的最大值是8. 若函数的最小值为m,则函数的最小值为( )A、 B、 C、 D、9. 已知函数 , 下列关于该函数的结论正确的是( )A、的图象关于直线对称 B、的一个周期是 C、在区间上单调递增 D、的最大值为10. 已知函数 , 则( )A、的定义域是 B、有最大值 C、不等式的解集是 D、在上单调递增11. 已知是函数的零点,则下列说法正确的是( )A、 B、 C、 D、12. 平面内到两定点距离之积为常数的点的轨迹称为卡西尼卵形线,它是1675年卡西尼在研究土星及其卫星的运行规律时发现的,已知在平面直角坐标系中, , , 动点P满足 , 则下列结论正确的是( )A、点的横坐标的取值范围是 B、的取值范围是 C、面积的最大值为 D、的取值范围是二、填空题
-
13. 已知 ,且 ,则 的最小值为.
14. 已知a , b∈R,且a–3b+6=0,则2a+ 的最小值为 .
15. 已知a∈R,函数f(x)=|x+ ﹣a|+a在区间[1,4]上的最大值是5,则a的取值范围是 .
16. 函数的最大值为 .17. 若点在函数的图象上,则的取值范围是 .18. 若 , 其中 , 则的最小值为.19. 平面上有一组互不相等的单位向量 , , …, , 若存在单位向量满足 , 则称是向量组 , , …,的平衡向量.已知 , 向量是向量组 , , 的平衡向量,当取得最大值时,值为 .20. 已知函数 , 其中 , 若不等式对任意恒成立,则的最小值为.21. 已知函数.若存在 , 使不等式成立,则整数的值可以为.(写出一个即可).22. 已知在上恒成立,则实数的最大值为 .23. 记正项数列的前项和为 , 且满足.若不等式恒成立,则实数的取值范围是.24. 如图,在矩形ABCD中, , AC与BD的交点为M,N为边AB上任意点(包含端点),则的最大值为 .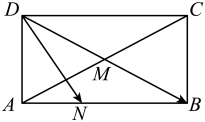 25. 已知函数 , 则在上的最大值与最小值之和为 .
25. 已知函数 , 则在上的最大值与最小值之和为 .三、解答题
-
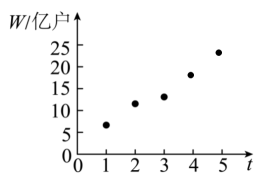
26. 已知函数 , .(1)、求的单调性;(2)、若函数在上有唯一零点,求实数a的取值范围.27. 已知函数.(1)、求不等式的解集;(2)、若 , , 求的取值范围.28. 已知函数.(1)、 , 解不等式;(2)、证明:.29. 已知函数 .(1)、求函数的单调区间;(2)、若对任意的 , 都有成立,求a的取值范围.30. 已知函数的最大值是.(1)、求的值;(2)、若( , ),求的最小值.31. 移动物联网广泛应用于生产制造、公共服务、个人消费等领域.截至2022年底,我国移动物联网连接数达18.45亿户,成为全球主要经济体中首个实现“物超人”的国家.右图是2018-2022年移动物联网连接数W与年份代码t的散点图,其中年份2018-2022对应的t分别为1~5.
附:样本相关系数 , , , ,
(1)、根据散点图推断两个变量是否线性相关.计算样本相关系数(精确到0.01),并推断它们的相关程度;(2)、(i)假设变量x与变量Y的n对观测数据为(x1 , y1),(x2 , y2),…,(xn,yn),两个变量满足一元线性回归模型 (随机误差).请推导:当随机误差平方和Q=取得最小值时,参数b的最小二乘估计.(ii)令变量 , 则变量x与变量Y满足一元线性回归模型利用(i)中结论求y关于x的经验回归方程,并预测2024年移动物联网连接数.
32. 已知函数(1)、当时,求不等式的解集;(2)、若 , 求的取值范围
