广东省潮州市潮安区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中，属于最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{25}$ D、 $\sqrt{3}$

查看试题解析
2. 某城市3月份某星期7天的最低气温如下（单位 $℃$ ）：16，20，18，16，18，18，17，这组数据的众数是（）

A、16 B、17 C、18 D、20

查看试题解析
3. 以下列各组数为边长的线段，可以组成直角三角形的是（）

A、2，2，3 B、4，5，7 C、5，12，13 D、10，10，10

查看试题解析
4. 关于菱形的性质，以下说法不正确的是（）

A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形

查看试题解析
5. 下列计算正确的是（）

A、 $2 \sqrt{3} + 4 \sqrt{2} = 6 \sqrt{5}$ B、 $\sqrt{8} = 4 \sqrt{2}$ C、 $\sqrt{27} \div \sqrt{3} = 3$ D、 $\sqrt{5} \times \sqrt{2} = 10$

查看试题解析
6. 下列各点中，在直线 $y = 2 x + 1$ 的是（）

A、 $(0 ， - \frac{1}{2})$ B、 $(- 3 ， - 2)$ C、 $(- 2 ， - 3)$ D、 $(\frac{1}{2} ， 0)$

查看试题解析
7. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ，若 $∠ A O B = 50 °$ ，则 $∠ O B C$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $20 °$ D、 $15 °$

查看试题解析
8. 如图，在▱ABCD中，BE平分∠ABC交DC于点E，若∠A=60°，则∠DEB的大小为（）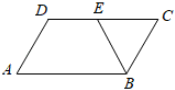

A、130° B、120° C、115° D、110°

查看试题解析
9. 如图，在平面直角坐标系中，点A和点B的坐标分别是： $A (- 2 ， 1)$ ， $B (2 ， 3)$ ．那么线段 $A B$ 的长度是（）

A、 $\sqrt{13}$ B、 $2 \sqrt{5}$ C、5 D、 $\sqrt{5}$

查看试题解析
10. 如图，直线 $y = - \frac{1}{2} x + 2$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 和点 $B$ ，点 $C$ 和点 $D$ 分别是线段 $O B$ ， $A B$ 的中点，点 $P$ 为线段 $O A$ 上的一动点，则 $P C + P D$ 值最小时点 $P$ 的坐标是（）

A、 $(2 ， 0)$ B、 $(\frac{7}{2} ， 0)$ C、 $(\frac{3}{2} ， 0)$ D、 $(1 ， 0)$

查看试题解析

二、填空题

11. 化简： $\sqrt{9}$ = ．

查看试题解析
12. “两直线平行，内错角相等”的逆命题是．

查看试题解析
13. 若二次根式 $\sqrt{a - 3}$ 有意义，则a的取值范围是．

查看试题解析
14. 某人沿直路行走，若此人离出发的距离s（千米）与行走时间t（分）的函数关系如图所示，则此人在这段时间内最快的行走速度是千米/分．

查看试题解析
15. 已知，在▱ABCD中， $A D = 2 A B$ ，点F为AD的中点，过点C作 $C E ⊥ A B$ ，垂足为点E，以下结论中，正确的是．
①CF是 $∠ B C D$ 的角平分线；②连接BF，则 $∠ B F C = 120 °$ ；③若 $∠ D = 60 °$ ，则 $S_{□ A B C D} = \sqrt{3} D C^{2}$ ；④连接EF，则 $E F = F C$ ．

查看试题解析

三、解答题

16. 计算： $\sqrt{20} - \sqrt{12} + \sqrt{5}$ ．

查看试题解析
17. 如图，在平行四边形 $A B C D$ 中，E，F分别是 $A B$ ， $C D$ 的中点，求证： $A F = C E$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于D， $A C = 5$ ， $B C = 9$ ， $A D = 4$ ，求 $A B$ 的长．

查看试题解析
19. 已知一次函数 $y = k x + b$ 的图象经过点 $(3 ， 5)$ 与 $(- 4 ， - 9)$ ，与x轴、y轴分别交于点A、点B．

(1)、求这个一次函数的解析式；

(2)、若坐标原点为O，求△ABO的面积．

查看试题解析
20. 为了进一步落实“双减”政策，某学校对本校初一学生“每天做家庭作业所用的大致时间（时间以整数记，单位：分钟）”做了抽样调查，并把调查所得到的所有数据（时间）进行整理，分成四个时间段，绘制成统计表和统计图（如下图）．请结合统计表和统计图中提供的信息，回答下面的问题：
作业时间/分钟
频率
$20 \leq x < 40$
0.10
$40 \leq x < 60$
0.30
$60 \leq x < 80$
a
$80 \leq x < 100$
0.25

(1)、本次抽样调查的样本容量是，统计表中a=；

(2)、请把统计图补充完整，并在图中标明相应数据；

(3)、这次调查得到的所有数据中位数落在了四个时间段中的段内．

查看试题解析
21. 一辆汽车和一辆摩托车分别从A、B两地前往同一个地方C城，它们距离A地的路程随着时间的变化的图象如图所示．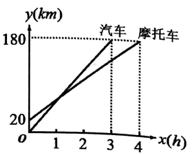

(1)、求摩托车整个过程中的平均速度．

(2)、如果两车同时出发，汽车在某处与摩托车相遇，求此时两车距离A地的距离．

(3)、如果摩托车到达C城后马上以原来的速度原路返回，求摩托车从B地出发5.5小时后与A地的距离．

查看试题解析
22. 如图1，在正方形 $A B C D$ 中，E是 $A B$ 的中点．

(1)、若 $A D = 4$ ，求 $D E$ 的长．

(2)、如图2，F是线段 $B C$ 上的一点，且 $A E = 2 B F$ ，求证： $△ D E F$ 是直角三角形．

(3)、如图3是一个正方体，棱长 $A D = 4$ ， $A B$ 的中点E处有一只蚂蚁，蚂蚁从 $E$ 处出发在正方体表面爬行，经过 $C D$ 上某点P处后继续沿直线方向爬到正方体的顶点G处．当 $E P + P G$ 的值最小时，求 $D P$ 的长．

查看试题解析
23. 如图所示，在平面直角坐标系中，直线 $y = x + 1$ 与x轴交于点B，直线 $y = - \frac{3}{4} x + 3$ 与x轴交于点C，与y轴交于点D．

(1)、直接写出点B、C的坐标：

(2)、点 $M (x ， y)$ 是直线 $y = x + 1$ 图象上一点，设 $△ B C M$ 的面积为S，请求出S关于x的函数关系式；并探究当点M运动到什么位置时（求出M点坐标即可）， $△ B C M$ 的面积为10，并说明理由．

(3)、线段CD上是否存在点P，使 $△ C B P$ 为等腰三角形，如果存在，求出点P的坐标；如果不存在，请说明理由．

查看试题解析

作业时间/分钟	频率
$20 \leq x < 40$	0.10
$40 \leq x < 60$	0.30
$60 \leq x < 80$	a
$80 \leq x < 100$	0.25