广东省广州市番禺区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
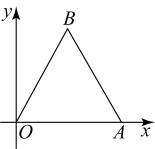
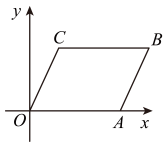
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列等式成立的是( )A、 B、 C、 D、3. 如图,等边的边长为2,则点B的坐标为( )
 A、 B、 C、 D、4. 已知的三边长分别为a , b , c , 在下列条件中,不能判断为直角三角形的是( )A、 , , B、 C、 , , D、5. 下列函数中,正比例函数是( )A、 B、 C、 D、6. 数据2、5、6、0、6、1、8的中位数和众数分别是( )A、0和6 B、0和8 C、5和6 D、5和87. 直线 向下平移2个单位,所得直线的解析式是( )A、 B、 C、 D、8. 如图,点O是对角线的交点,EF过点O分别交、于点E、F , 下列结论中成立的是( )
A、 B、 C、 D、4. 已知的三边长分别为a , b , c , 在下列条件中,不能判断为直角三角形的是( )A、 , , B、 C、 , , D、5. 下列函数中,正比例函数是( )A、 B、 C、 D、6. 数据2、5、6、0、6、1、8的中位数和众数分别是( )A、0和6 B、0和8 C、5和6 D、5和87. 直线 向下平移2个单位,所得直线的解析式是( )A、 B、 C、 D、8. 如图,点O是对角线的交点,EF过点O分别交、于点E、F , 下列结论中成立的是( )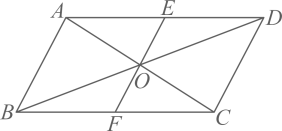 A、 B、 C、 D、9. 如图①,在长方形 中,动点R从点N出发,沿 方向运动至点M处停止,设点R运动的路程为x, 的面积为y,如果y关于x的函数图象如图②所示,那么当 时,点R应运动到( )
A、 B、 C、 D、9. 如图①,在长方形 中,动点R从点N出发,沿 方向运动至点M处停止,设点R运动的路程为x, 的面积为y,如果y关于x的函数图象如图②所示,那么当 时,点R应运动到( )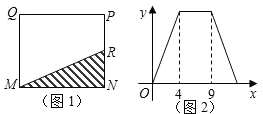 A、点N处 B、点P处 C、点Q处 D、点M处10. 如图,在矩形ABCD中, , , E是BC的中点,将沿直线AE翻折,点B落在点F处,连接CF , 则CF的长为( )
A、点N处 B、点P处 C、点Q处 D、点M处10. 如图,在矩形ABCD中, , , E是BC的中点,将沿直线AE翻折,点B落在点F处,连接CF , 则CF的长为( )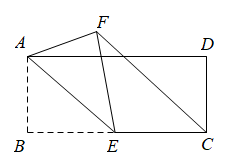 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若二次根式 有意义,则x的取值范围是12. 在平面直角坐标系中,两点和之间的距离 .13. 如图,将平行四边形放置在平面直角坐标系中,O为坐标原点,若点A的坐标是 , 点C的坐标是 , 则点B的坐标是 .
 14. 如图是“赵爽弦图”,其中、、和是四个全等的直角三角形,四边形和都是正方形.如果 , , 那么等于 .
14. 如图是“赵爽弦图”,其中、、和是四个全等的直角三角形,四边形和都是正方形.如果 , , 那么等于 .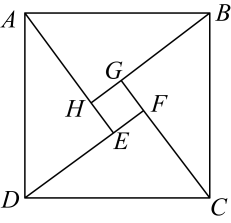 15. 甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温的方差大小关系为(填或).
15. 甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温的方差大小关系为(填或). 16. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)
16. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)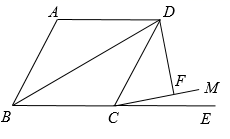
三、解答题
-
17. 计算:(1)、;(2)、;(3)、 .18. 如图,O为坐标原点,一次函数的图象与x轴、y轴分别相交于A、B两点,半径为2的经过A、B两点.
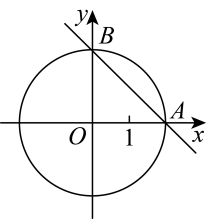 (1)、写出A、B两点的坐标;(2)、求此一次函数的解析式;(3)、求圆心O到直线的距离.19. 如图,BD是▱ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
(1)、写出A、B两点的坐标;(2)、求此一次函数的解析式;(3)、求圆心O到直线的距离.19. 如图,BD是▱ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.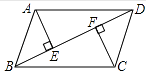 20. 下图统计的是一个路口某时段来往车辆的车速情况,请运用你所学的统计知识,写一份简短的报告,让交警知道在这个时段,该路口来往车辆的车速情况(如最大车速,车速数据的中位数、众数、平均数等),并对数据作一个简要分析.
20. 下图统计的是一个路口某时段来往车辆的车速情况,请运用你所学的统计知识,写一份简短的报告,让交警知道在这个时段,该路口来往车辆的车速情况(如最大车速,车速数据的中位数、众数、平均数等),并对数据作一个简要分析.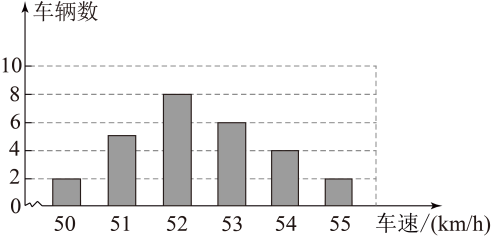 21. 为了锻炼身体增强体质,小何同学在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知小何离家的距离s(km)与时间t(h)之间的关系如图所示.
21. 为了锻炼身体增强体质,小何同学在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知小何离家的距离s(km)与时间t(h)之间的关系如图所示.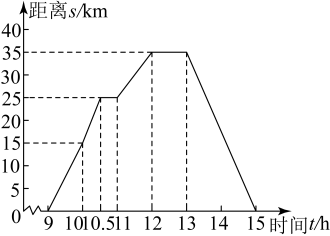
根据图象解答下列问题:
(1)、写出小何离家的最远距离;(2)、小何途中共休息了几次,每次休息多长时间?(3)、小何由离家最远的地方返回家时的平均速度是多少?22. 如图,函数与的图象交于点 .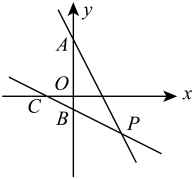 (1)、求出m , n的值;(2)、观察图象,写出的解集;(3)、设和的面积分别为、 , 求 .23. 如图,菱形的对角线、相交于点 , 过点作 , 且 , 连接交于点 , 连接、 .
(1)、求出m , n的值;(2)、观察图象,写出的解集;(3)、设和的面积分别为、 , 求 .23. 如图,菱形的对角线、相交于点 , 过点作 , 且 , 连接交于点 , 连接、 .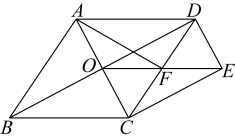 (1)、求证:;(2)、若菱形的边长为 , , 求 .24. 某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有一名教师,现有甲、乙两种大客车,它们的载客量和租金如下表所示.
(1)、求证:;(2)、若菱形的边长为 , , 求 .24. 某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有一名教师,现有甲、乙两种大客车,它们的载客量和租金如下表所示.甲种大客车
乙种大客车
载客量(人/辆)
45
30
租金(元/辆)
400
280
设共租用了汽车m辆,其中租用甲种客车x辆,租车费用为y元.
(1)、求y关于x的函数解析式;(2)、运用上述关系,求出最节省费用的租车方案,并说明理由.25. 如图,点是正方形边上一动点(不与、重合),是外角的平分线,点在射线上.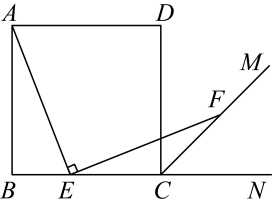 (1)、当时,判断与是否垂直,并证明结论;(2)、若在点运动过程中,线段与始终满足关系式 .
(1)、当时,判断与是否垂直,并证明结论;(2)、若在点运动过程中,线段与始终满足关系式 .①连接 , 证明的值为常量;
②设与的交点为 , 的周长为 , 求正方形的面积.