广东省广州市海珠区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
1. 一组数据3,5,4,6,3,3,4的众数是( )A、3 B、4 C、5 D、62. 若二次根式有意义,则x的取值范围是( )A、 B、 C、 D、3. 如图,是的中位线,若 , 则( )
 A、2 B、4 C、6 D、84. 已知点在一次函数的图象上,则等于( ).A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,一架靠墙摆放的梯子长5米,底端离墙脚的距离为3米,则梯子顶端离地面的距离为( )米.
A、2 B、4 C、6 D、84. 已知点在一次函数的图象上,则等于( ).A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,一架靠墙摆放的梯子长5米,底端离墙脚的距离为3米,则梯子顶端离地面的距离为( )米. A、5 B、4 C、3 D、27. 在中, , , , 点是的中点,则( )cmA、6.5 B、6 C、5.5 D、58. 已知数据 , , , , 的平均数为 , 则的值是( )A、 B、 C、 D、9. 已知点 , 在一次函数的图象上,若 , 则与的大小关系是( )A、 B、 C、 D、无法确定10. 菱形在平面直角坐标系中的位置如图所示,点的坐标为 , , 则点的坐标为( )
A、5 B、4 C、3 D、27. 在中, , , , 点是的中点,则( )cmA、6.5 B、6 C、5.5 D、58. 已知数据 , , , , 的平均数为 , 则的值是( )A、 B、 C、 D、9. 已知点 , 在一次函数的图象上,若 , 则与的大小关系是( )A、 B、 C、 D、无法确定10. 菱形在平面直角坐标系中的位置如图所示,点的坐标为 , , 则点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 某班将从甲、乙两位学生中选派一人参加学校的环保知识决赛,经过两轮测试,他们的平均成绩都是87分,方差分别是 , , 你认为成绩更稳定的选手是(填“甲”或“乙”).12. “如果 , 那么”的逆命题是.13. 一组数据1,6,7,4,7,5,2的中位数是 .14. 若菱形的两条对角线的长分别为4和5,则此菱形的面积是 .15. 若 , 则式子的值为 .16. 已知一次函数的图象经过第一、二、四象限,则的取值范围为 .
三、解答题
-
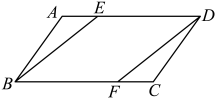
17. 计算:(1)、;(2)、18. 如图,在中,分别在边上,且 , 求证:四边形是平行四边形.
 19. 已知正比例函数 .
19. 已知正比例函数 . (1)、该直线向下平移个单位,平移后所得直线的解析式为;(2)、在图中画出平移后的直线.20. 为了提高节能意识,某中学对全校的耗电情况进行了抽样调查,并记录了10天的耗电量情况,数据如表:
(1)、该直线向下平移个单位,平移后所得直线的解析式为;(2)、在图中画出平移后的直线.20. 为了提高节能意识,某中学对全校的耗电情况进行了抽样调查,并记录了10天的耗电量情况,数据如表:度数(度)
250
300
350
400
450
天数
1
2
3
2
(1)、表格中的;(2)、求出这10天的平均耗电量;(3)、若每度电的定价是0.6元,根据(2)所获得的数据,请估计该中学每月应付电费多少元?(每月按30天计)21. 如图,在中, , , , 平分交于点 . (1)、求的面积;(2)、求的长.22. 如图,在四边形中,对角线与相交于点 , 是的中点, .
(1)、求的面积;(2)、求的长.22. 如图,在四边形中,对角线与相交于点 , 是的中点, . (1)、请你从以下条件①;②;③平分;④中,选择一个使得四边形是菱形的条件 . (填序号);(2)、根据(1)中所选择的条件,求证:四边形是菱形.23. 某动物园在周年庆来临之际,推出、两种纪念章,已知每个种纪念章的进价比每个种纪念章的进价多4元;购进6件种纪念章和购进10件种纪念章的费用相同,且种纪念章售价为13元/个,种纪念章售价为8元/个.(1)、每个种纪念章和每个种纪念章的进价分别是多少元?(2)、根据网上预约的情况,该园计划用不超过2800元的资金购进、两种纪念章共400个,这400个纪念章可以全部销售,选择哪种进货方案,该园获利最大?最大利润是多少元?24. 如图,已知直线:和直线:相交于点 , 直线与轴相交于点 , 与轴相交于点 .
(1)、请你从以下条件①;②;③平分;④中,选择一个使得四边形是菱形的条件 . (填序号);(2)、根据(1)中所选择的条件,求证:四边形是菱形.23. 某动物园在周年庆来临之际,推出、两种纪念章,已知每个种纪念章的进价比每个种纪念章的进价多4元;购进6件种纪念章和购进10件种纪念章的费用相同,且种纪念章售价为13元/个,种纪念章售价为8元/个.(1)、每个种纪念章和每个种纪念章的进价分别是多少元?(2)、根据网上预约的情况,该园计划用不超过2800元的资金购进、两种纪念章共400个,这400个纪念章可以全部销售,选择哪种进货方案,该园获利最大?最大利润是多少元?24. 如图,已知直线:和直线:相交于点 , 直线与轴相交于点 , 与轴相交于点 . (1)、求点的坐标;(2)、点在直线上,在直线上是否存在点 , 使以点、、、为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点的坐标:若不存在,请说明理由.(3)、直线:经过一定点 , 与轴相交于点 , 若直线把的面积分成两部分,求定点的坐标和的值.25. 已知在正方形中,
(1)、求点的坐标;(2)、点在直线上,在直线上是否存在点 , 使以点、、、为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点的坐标:若不存在,请说明理由.(3)、直线:经过一定点 , 与轴相交于点 , 若直线把的面积分成两部分,求定点的坐标和的值.25. 已知在正方形中, (1)、如图1,点、分别为、边上的动点,且 , 连接、交于点 , 点为正方形对角线的交点.
(1)、如图1,点、分别为、边上的动点,且 , 连接、交于点 , 点为正方形对角线的交点.①猜想线段与之间有怎样的数量和位置关系?请直接写出你的猜想,不需证明;
②下列结论:甲同学认为的值不变;乙同学认为:的值不变,其中只有一个结论正确,请选择正确的结论并求其值;
(2)、如图2,是等腰三角形, , 求证: .