广东省广州市海珠区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
1. 16的算术平方根是( )A、4 B、 C、 D、2. 不等式的解集在数轴上表示正确的是()A、
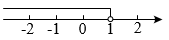 B、
B、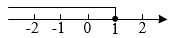 C、
C、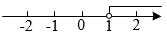 D、
D、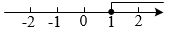 3. 下列几组解中,二元一次方程的解是( )A、 B、 C、 D、4. 为了了解我市八年级学生每天用于学习的时间,对其中500名学生进行了随机调查,则下列说法错误的是( )A、总体是我市八年级学生每天用于学习的时间的全体 B、其中500名学生是总体的一个样本 C、样本容量是500 D、个体是我市八年级学生中每名学生每天用于学习的时间5. 下列说法正确的是( )A、相等的角是对顶角 B、两个锐角的和是锐角 C、邻补角互补 D、同旁内角互补6. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
3. 下列几组解中,二元一次方程的解是( )A、 B、 C、 D、4. 为了了解我市八年级学生每天用于学习的时间,对其中500名学生进行了随机调查,则下列说法错误的是( )A、总体是我市八年级学生每天用于学习的时间的全体 B、其中500名学生是总体的一个样本 C、样本容量是500 D、个体是我市八年级学生中每名学生每天用于学习的时间5. 下列说法正确的是( )A、相等的角是对顶角 B、两个锐角的和是锐角 C、邻补角互补 D、同旁内角互补6. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( ) A、60° B、50° C、40° D、30°7. 若成立,则下列不等式成立的是( )A、 B、 C、 D、8. 若点在第二象限,则点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知关于、的方程组的解满足 , 则的值为( )A、 B、2 C、 D、10. 如图,一个机器人从点O出发,向正西方向走到达点;再向正北方向走到达点;再向正东方向走到达点;再向正南方向走到达点;再向正西方向走到达点 , 按如此规律走下去,当机器人走到点时,点的坐标为( )
A、60° B、50° C、40° D、30°7. 若成立,则下列不等式成立的是( )A、 B、 C、 D、8. 若点在第二象限,则点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知关于、的方程组的解满足 , 则的值为( )A、 B、2 C、 D、10. 如图,一个机器人从点O出发,向正西方向走到达点;再向正北方向走到达点;再向正东方向走到达点;再向正南方向走到达点;再向正西方向走到达点 , 按如此规律走下去,当机器人走到点时,点的坐标为( )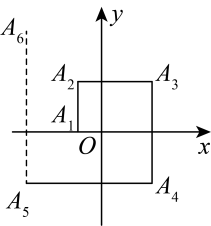 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点(-2,3)向右平移2个单位后的坐标为.12. 已知2x+y=3,用关于x的代数式表示y,则y=。13. 比较大小:3(填“”、“”或“”).14. 小明借到一本有72页的图书,要在10天内读完,开始2天每天只读5页,设以后几天每天读页,所列不等式为 .15. 如图,将沿着点B到C的方向平移到的位置, , , 平移距离为 , 则阴影部分面积为 .
 16. 关于的不等式组有3个整数解,则的取值范围是 .
16. 关于的不等式组有3个整数解,则的取值范围是 .三、解答题
-
17. 计算:(1)、(2)、18.(1)、解二元一次方程组(2)、解不等式组19. 如图,在平面直角坐标系中,的顶点坐标分别是 , , .
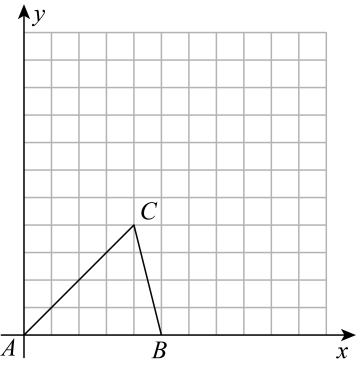 (1)、将向上平移2个单位长度,再向右平移3个单位长度,得到 , 请在平面直角坐标系中画出平移后的;(2)、直接写出点的坐标;(3)、求的面积.20. 如图,已知 , 平分交于点 .
(1)、将向上平移2个单位长度,再向右平移3个单位长度,得到 , 请在平面直角坐标系中画出平移后的;(2)、直接写出点的坐标;(3)、求的面积.20. 如图,已知 , 平分交于点 . (1)、求证:;(2)、若于点 , , 求的度数.21. 端午节是我国的传统佳节,民间历来有吃“粽子”的习俗.某食品厂为了解方民对去年销量较好的肉馅、豆沙馅、花生馅、蜜枣馅四种不同口味粽子的喜爱情况,在节前对某居民区方民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)、求证:;(2)、若于点 , , 求的度数.21. 端午节是我国的传统佳节,民间历来有吃“粽子”的习俗.某食品厂为了解方民对去年销量较好的肉馅、豆沙馅、花生馅、蜜枣馅四种不同口味粽子的喜爱情况,在节前对某居民区方民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答: (1)、本次参加抽样调查的居民人数是人(2)、将图①②补充完整;(直接补填在图中)(3)、求图②中表示“”的圆心角的度数;(4)、若居民区有10000人,请估计爱吃蜜枣馅粽子的人数.22. 某电器超市销售每台进价分别为160元、120元的、两种型号的电风扇,已知2台型和3台型电风扇可卖850元;5台型和6台型电风扇可卖1900元.(1)、求、两种型号的电风扇的销售单价;(2)、若超市准备再采购这两种型号的电风扇共50台,销售完这50台电风扇能实现利润超过1700元的目标,求最多采购型风扇多少台?23. 如图,平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点坐标为 .
(1)、本次参加抽样调查的居民人数是人(2)、将图①②补充完整;(直接补填在图中)(3)、求图②中表示“”的圆心角的度数;(4)、若居民区有10000人,请估计爱吃蜜枣馅粽子的人数.22. 某电器超市销售每台进价分别为160元、120元的、两种型号的电风扇,已知2台型和3台型电风扇可卖850元;5台型和6台型电风扇可卖1900元.(1)、求、两种型号的电风扇的销售单价;(2)、若超市准备再采购这两种型号的电风扇共50台,销售完这50台电风扇能实现利润超过1700元的目标,求最多采购型风扇多少台?23. 如图,平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点坐标为 . (1)、当点在轴上时,求的面积;(2)、当点在第一象限时,用含的式子表示的面积.24. 如图,直线 , 点为直线上的一个定点,点为直线、之间的定点,点为直线上的动点.
(1)、当点在轴上时,求的面积;(2)、当点在第一象限时,用含的式子表示的面积.24. 如图,直线 , 点为直线上的一个定点,点为直线、之间的定点,点为直线上的动点.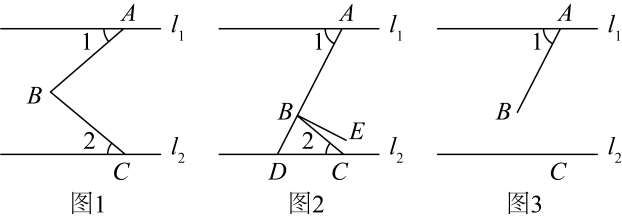 (1)、当点运动到图1所示位置时,求证:;(2)、点在直线上,且 , 平分 .
(1)、当点运动到图1所示位置时,求证:;(2)、点在直线上,且 , 平分 .①如图2,若点在的延长线上, , 求的度数;
②若点不在的延长线上,且点在直线的右侧,请直接写出与之间的数量关系.(本问中的角均为小于的角)
25. 【材料阅读】二元一次方程有无数组解,如: , , , , 如果我们将方程的解看成一组有序数对,那么这些有序数对可以用平面直角坐标系中的点表示,探究发现:以方程的解为坐标的点落在同一条直线上,如图1所示,同时这条直线上的点的坐标全都是该方程的解.我们把这条直线称为该方程的图象.
 (1)、【问题探究】
(1)、【问题探究】请在图2中画出二元一次方程组中的两个二元一次方程的图象,并直接写出该方程组的解为 ▲ ;
(2)、已知关于 , 的二元一次方程无解,请在图3中画出符合题意的两条直线,设方程①图象与 , 轴的交点分别是、 , 方程②图象与 , 轴的交点分别是、 , 计算的度数.(3)、【拓展应用】图4中包含关于 , 的二元一次方程组的两个二元一次方程的图象,请直接写出该方程组的解。