广东省广州市南沙区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，为最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{3}$ C、 $\sqrt{4}$ D、 $\sqrt{12}$

查看试题解析
2. 下列各组数中，不能构成直角三角形的一组是（）

A、5，7，10 B、3，4，5 C、6，8，10 D、 $1 ， 2 ， \sqrt{3}$

查看试题解析
3. 在四边形 $A B C D$ 中， $A B ∥ D C$ ，当满足下列哪个条件时，可以得出四边形 $A B C D$ 是平行四边形（）

A、 $∠ A ＋ ∠ C ＝ 180 °$ B、 $∠ B ＋ ∠ D ＝ 180 °$ C、 $∠ A ＋ ∠ B ＝ 180 °$ D、 $∠ A ＋ ∠ D ＝ 180 °$

查看试题解析
4. 已知函数 $y = (k - 3) x$ 是正比例函数，且y随着x的增大而减小，则下面判断正确的是（）

A、 $k > 0$ B、 $k < 0$ C、 $k > 3$ D、 $k < 3$

查看试题解析
5. 若甲、乙、丙、丁四位同学在八年级第一学期4次数学测试的平均成绩恰好都是85分，方差分别为 ${s_{甲}}^{2} = 0.80$ ， ${s_{乙}}^{2} = 1.75$ ， ${s_{丙}}^{2} = 0.32$ ， ${s_{丁}}^{2} = 1.26$ ，则成绩最稳定的同学是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 菱形 $A B C D$ 的对角线 $A C = 4$ ， $∠ D = 60 °$ ，则对角线 $B D$ 的长是（）

A、 $4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、4 D、2

查看试题解析
7. 如图，一个工人拿一个2.5米长的梯子，底端A放在距离墙根C $0.7$ 米处，另一头B点靠墙，如果梯子的顶部下滑0.4米，梯子的底部向外滑多少米？（）

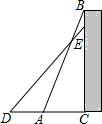A、0.4 B、0.6 C、0.7 D、0.8

查看试题解析
8. 如果 $\sqrt{{(2 a - 1)}^{2}} = 2 a - 1$ ，且a是非负数，则（）

A、 $0 < a < \frac{1}{2}$ B、 $0 ≤ a ≤ \frac{1}{2}$ C、 $a \geq \frac{1}{2}$ D、 $0 < a \leq \frac{1}{2}$

查看试题解析
9. 若正比例函数 $y = k x$ 的图象经过第二、第四象限，常数k和b互为相反数，则一次函数 $y = k x - b$ 在平面直角坐标系中的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，点B ， C ， E在同一直线上，分别以 $B C ， C E$ 为边作正方形 $A B C D$ 和正方形 $C E F G$ ， $B C = 2 ， C E = 4$ ， H是 $A F$ 的中点，那么 $C H$ 的长是（）

A、 $2 \sqrt{2}$ B、 $\sqrt{10}$ C、 $2 \sqrt{10}$ D、 $4 \sqrt{2}$

查看试题解析

二、填空题

11. 计算： $\sqrt{8} - \sqrt{2}$ = ．

查看试题解析
12. 直线 $y = - 2 x + 4$ 的图象一定不经过第象限．

查看试题解析
13. 在直角坐标系中，点 $P (- 3 ， 2)$ 到原点的距离是．

查看试题解析
14. 若一组数据：1，7，8，a ， 4的平均数是5，中位数是．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 6 ， B C = 8$ ， $∠ A B D$ 的平分线与边 $A D$ 交于点E ，则 $D E$ 的长是．

查看试题解析
16. 直线 $y = - 2 x + m$ 与直线 $y = x - 1$ 的交点在第四象限内，则m的取值范围是．

查看试题解析

三、解答题

17. 计算： $\sqrt{3} (\sqrt{12} + 1)$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A = 55 °$ ， $∠ C = 35 °$ ， $A C = 4$ ， $B C = 3$ ，求 $A B$ 的长．

查看试题解析
19. 周长为20cm的矩形，若它的一边长是xcm，面积是Scm²

(1)、请用含x的式子表示S ，并指出常量与变量；

(2)、当 $x = 6$ 时，求S的值．

查看试题解析
20. 如图， $A E ∥ B F$ ， $∠ B A E$ 的平分线交 $B F$ 于点 $C$ ，点 $D$ 在 $A E$ 上， $A B = A D$ ，连接 $C D$ ．求证：四边形 $A B C D$ 是菱形．

查看试题解析
21. 请阅读下面的材料，并探索用材料中的方法解决问题．
【材料1】两个含有二次根式而非零的代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式．

例如： $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) = 1$ ，我们称 $\sqrt{3} + \sqrt{2}$ 的一个有理化因式是 $\sqrt{3} - \sqrt{2}$ ．

【材料2】如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含根号，这种变形叫做分母有理化．

例如： $\frac{2}{\sqrt{3} + \sqrt{2}} = \frac{2 (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \frac{2 (\sqrt{3} - \sqrt{2})}{1} = 2 \sqrt{3} - 2 \sqrt{2}$ ．

问题探究：

(1)、写出 $\sqrt{5} - \sqrt{7}$ 的一个有理化因式：_；

(2)、计算： $(2 \sqrt{3} + 3 \sqrt{2}) (2 \sqrt{3} - 3 \sqrt{2}) - {(\sqrt{3} + \sqrt{2})}^{2}$ ；

(3)、将式子 $\frac{22}{2 \sqrt{5} + 3}$ 分母有理化．

查看试题解析

22. 某渔业养殖户在自家鱼塘中放养了某种鱼2000条，若干年后，准备打捞出售，为了估计鱼塘中这种鱼的总质量，现从鱼塘中捕捞三次，得到数据如下表：

	鱼的条数（条）	平均每条鱼的质量（千克）
第一次	30	2.8
第二次	40	3
第三次	30	3.2

(1)、求鱼塘中这种鱼平均每条的重量．

(2)、若这种鱼放养的成活率是

85 %

，请估计鱼塘中这种鱼的总重量．（新生鱼和死鱼不计算入内．）

(3)、如果把鱼塘中放养的2000条中存活的这种鱼全部卖掉，价格为每千克20元，若投资成本为45000元，求卖出后获得的纯利润．

查看试题解析

23. 一次函数 $y = k x + 2$ 的图象与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $C$ ．一次函数 $y = - x + 4$ 的图象与 $x$ 轴交于点 $B$ ，与 $y$ 轴交于点 $D$ ．两函数图象交于点 $P (m ， 3)$ ．

(1)、求 $k$ 和 $m$ 的值；

(2)、求线段 $A P$ 的长；

(3)、若直线 $A C$ 上有一动点 $Q$ ，过 $Q$ 作直线 $Q H$ ， $Q H$ 平行于 $y$ 轴， $Q H$ 直线 $B D$ 于点 $H$ ．当 $Q H = O B$ 时，求 $Q$ 的坐标．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6 c m$ ， $A B = 10 c m$ ．动点P从点A出发，沿着A→C→B→A的路径，以每秒 $2 c m$ 的速度运动，当P回到A点时运动结束，设点P运动的时间为t秒．

(1)、当 $t = 2$ 时，求 $△ B P C$ 的面积；

(2)、若 $A P$ 平分 $∠ C A B$ ，求t的值；

(3)、深入探索：若点P运动到边 $A B$ ，且 $△ A C P$ 是等腰三角形，求t的值．

查看试题解析
25. 已知，如图①，在 $▱ A B C D$ 中， $∠ A = 90 °$ ， $A B = B C = 4$ $\sqrt{5}$ ，点E为 $C D$ 上的一动点，连接 $B E$ ，过点C作 $C H ⊥ B E$ 于点H ，以 $C H$ 为腰作等腰直角 $△ H C G ， ∠ H C G = 90 ° ，$ 连接 $D H$ ．

(1)、求证：四边形 $A B C D$ 为正方形；

(2)、如图②，当D ， H ， G三点共线时，求 $D H^{2} + D G^{2}$ 的值；

(3)、求 $D H$ 的最小值．

查看试题解析