广东省河源市紫金县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、a2•a3=a6 B、(a2)3=a5 C、(ab)3=a3b3 D、a8÷a2=a42. 美术老师布置同学们设计窗花,下列作品为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 生物学家发现一种病毒的长度约为 , 将数“”用科学记数法表示为( )A、 B、 C、 D、4. 如果一个角是 , 那么它的补角等于( )A、 B、 C、 D、5. 如图,两条平行线a,b被第三条直线c所截.若 , 则的度数为( )
3. 生物学家发现一种病毒的长度约为 , 将数“”用科学记数法表示为( )A、 B、 C、 D、4. 如果一个角是 , 那么它的补角等于( )A、 B、 C、 D、5. 如图,两条平行线a,b被第三条直线c所截.若 , 则的度数为( ) A、 B、 C、 D、6. 对于圆的面积公式 , 下列说法中,正确的为( )A、是自变量 B、R是常量 C、R是自变量 D、和R是都是常量7. 下列长度的三条线段,能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,8. 如图,△ABC≌△DEC,点B,C,D在同一条直线上,且CE=2,CD=4,则BD的长为( )
A、 B、 C、 D、6. 对于圆的面积公式 , 下列说法中,正确的为( )A、是自变量 B、R是常量 C、R是自变量 D、和R是都是常量7. 下列长度的三条线段,能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,8. 如图,△ABC≌△DEC,点B,C,D在同一条直线上,且CE=2,CD=4,则BD的长为( )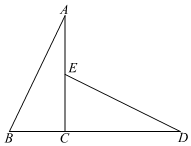 A、1.5 B、2 C、4.5 D、69. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 交于点 , 连接 , 则的度数为( )
A、1.5 B、2 C、4.5 D、69. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 交于点 , 连接 , 则的度数为( ) A、 B、 C、 D、10. 在一个不透明的口袋中装有3个红球,5个白球和若干个黑球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到白球的频率稳定在25%附近,则口袋中黑球的个数可能是( )A、10 B、11 C、12 D、13
A、 B、 C、 D、10. 在一个不透明的口袋中装有3个红球,5个白球和若干个黑球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到白球的频率稳定在25%附近,则口袋中黑球的个数可能是( )A、10 B、11 C、12 D、13二、填空题
-
11. 计算: .12. 如下图, , 则的度数是
 13. 如果把一枚质地均匀的骰子抛到桌面上,那么正面朝上的数字是偶数的概率是 .14. 已知代数式是完全平方式,则的值为 .15. 如图,在四边形中, , 为的中点,且平分 . 若 , , 则 .
13. 如果把一枚质地均匀的骰子抛到桌面上,那么正面朝上的数字是偶数的概率是 .14. 已知代数式是完全平方式,则的值为 .15. 如图,在四边形中, , 为的中点,且平分 . 若 , , 则 .
三、解答题
-
16. 先化简,再求值; , 其中 .17. 如图,在中,点E , F在上,且 . 点D为平面内一点,且满足 , .
求证: .
 18. 如图,已知△ABC.
18. 如图,已知△ABC.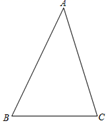 (1)、请用尺规作图作出AC的垂直平分线,垂足为点D,交AB于点E(保留作图痕迹,不要求写作法).(2)、连接CE,如果△ABC的周长为32,DC的长为6,求△BCE的周长.19. 一个不透明的箱子里装有红、黄、蓝三种颜色的小球共30个,它们除颜色外其他均相同,其中红色球有6个、黄色球有16个.(1)、求摸出1个球是蓝色球的概率;(2)、再往箱子中放入多少个蓝色球,可以使摸出1个蓝色球的概率为?20. 在学习地理时,我们知道:“海拔越高,气温越低”下表是海拔高度与此高度处气温之间的关系.
(1)、请用尺规作图作出AC的垂直平分线,垂足为点D,交AB于点E(保留作图痕迹,不要求写作法).(2)、连接CE,如果△ABC的周长为32,DC的长为6,求△BCE的周长.19. 一个不透明的箱子里装有红、黄、蓝三种颜色的小球共30个,它们除颜色外其他均相同,其中红色球有6个、黄色球有16个.(1)、求摸出1个球是蓝色球的概率;(2)、再往箱子中放入多少个蓝色球,可以使摸出1个蓝色球的概率为?20. 在学习地理时,我们知道:“海拔越高,气温越低”下表是海拔高度与此高度处气温之间的关系.海拔高度
0
1
2
3
4
5
气温
20
14
8
2
(1)、当气温为时,海拔高度是;(2)、写出气温与海拔高度之间的关系式;(3)、当气温是时,求海拔高度.21. 为了测量一幢高楼的高 , 在旗杆与楼之间选定一点 . 测得旗杆顶的视线与地面的夹角 , 测楼顶的视线与地面的夹角 , 量得点到楼底距离与旗杆高度相等,等于8米,量得旗杆与楼之间距离为米,求楼高是多少米?