广东省揭阳市榕城区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 把点 $(2 ， - 3)$ 先向左平移3个单位长度，再向上平移2个单位长度得到的点的坐标是在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 若 $\frac{| x | - 2}{x + 2}$ 的值等于0，则x的值是（）

A、2 B、 $- 2$ C、2或 $- 2$ D、0

查看试题解析
3. 已知 $x - y = - 2$ ， $x y = 3$ ，则 $x^{2} y - x y^{2}$ 的值为（）

A、2 B、-6 C、5 D、-36

查看试题解析
4. 下列各式中，能用平方差公式分解因式的是（）

A、 $x^{2} + 4 y^{2}$ B、 $x^{2} + 2 x - 1$ C、 $- x^{2} - 4 y^{2}$ D、 $- x^{2} + 4 y^{2}$

查看试题解析
5. 在平面直角坐标系中， $▱ A B C D$ 的顶点 $A$ ， $B$ ， $D$ 的坐标分别是 $(0 ， 0)$ ， $(5 ， 0)$ ， $(2 ， 3)$ ，则顶点 $C$ 的坐标是（）

A、 $(3 ， 7)$ B、 $(5 ， 3)$ C、 $(7 ， 3)$ D、 $(8 ， 2)$

查看试题解析
6. 不等式组 ${\begin{matrix} 1 - 2 x < 3 \\ \frac{x + 1}{2} \leq 2 \end{matrix}$ 的正整数解的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
7. 如图，数轴上点 $A$ 、 $B$ 、 $C$ 表示的数分别为 $- 4$ ， $- 2$ 和3，点 $O$ 为原点，则以 $O A$ 、 $O C$ 、 $B C$ 为边长构造三角形，则构造的三角形为（）

A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
8. 若关于x的分式方程 $\frac{x - 1}{x + 1} = \frac{a}{x + 1} - 2$ 有增根，则a的值是（）

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析
9. 如图，在 $△ A B C$ 中， $A I$ 平分 $∠ B A C$ ， $B I$ 平分 $∠ A B C$ ，点 $O$ 是 $A C$ 、 $B C$ 的垂直平分线的交点，连接 $A O$ 、 $B O$ ，若 $∠ A O B = 140 °$ ，则 $∠ A I B$ 的大小为（）

A、 $90 °$ B、 $105 °$ C、 $125 °$ D、 $145 °$

查看试题解析
10. 如图， $△ A B C$ 中， $A B = 8 c m ， A C = 6 c m$ ，点E是 $B C$ 的中点，若 $A D$ 平分 $∠ B A C$ ， $C D ⊥ A D$ ，线段 $D E$ 的长为（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析

二、填空题

11. 分解因式： $a^{3} - 2 a^{2} =$ ．

查看试题解析
12. 如图，用含x的不等式表示数轴上所表示的解集．

查看试题解析
13. 如图，∠C＝90°，将直角三角形ABC沿着射线BC方向平移6cm，得三角形A′B′C′，已知BC＝3cm，AC＝4cm，则阴影部分的面积为cm².

查看试题解析
14. 关于 $x$ 的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 的解为负数，则 $m$ 的取值范围是．

查看试题解析
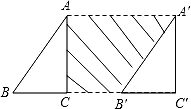15. 编程兴趣小组为半径为0.2米的圆形扫地机器人编制了如图所示的程序，若扫地机器人在无障碍的实验室平地上按照编制的程序扫地，则这个扫地机器人扫过的实验室平地的面积是米 $^{2}$ ．

查看试题解析

三、解答题

16. 解不等式组 ${\begin{array}{l} x + 5 \leq 0 ， \\ \frac{3 x - 1}{2} \geq 2 x + 1 ． \end{array}$

查看试题解析
17. 解方程： $\frac{x - 8}{x - 7} - \frac{1}{7 - x} = 8$ ．

查看试题解析
18. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，EB平分∠DEC.

(1)、求证：BC=CE；

(2)、若CE=AB，EA=EB，求∠C的度数.

查看试题解析
19. 先化简，再求值： $(1 - \frac{2}{a - 1}) \div \frac{a^{2} - 6 a + 9}{a - 1}$ ，从 $- 1 ， 1 ， 3$ 中选择一个合适的 $a$ 的值代入求值．

查看试题解析
20. 教材中这样写道：“我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式”，如果关于某一字母的二次多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．
例如：分解因式 $x^{2} + 2 x - 3$ ．

$\begin{matrix} 原式 = (x^{2} + 2 x + 1) - 4 = (x + 1)^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1) ； \end{matrix}$

例如：求代数式 $x^{2} + 4 x + 6$ 的最小值．

原式 $= x^{2} + 4 x + 4 + 2 = (x + 2)^{2} + 2$ ．

$∵ (x + 2)^{2} \geq 0 ，$

$∴$ 当 $x = - 2$ 时， $x^{2} + 4 x + 6$ 有最小值是2．

根据阅读材料用配方法解决下列问题：

(1)、分解因式： $m^{2} - 4 m - 5 =$ ；

(2)、若 $y = - x^{2} + 2 x - 3$ ，当 $x =$ 时， $y$ 有最值（填“大”或“小”），这个值是；

(3)、当 $a ， b ， c$ 分别为 $△ A B C$ 的三边时，且满足 $a^{2} + b^{2} + c^{2} - 6 a - 10 b - 8 c + 50 = 0$ 时，判断 $△ A B C$ 的形状并说明理由．

查看试题解析

21. 证明：三角形的中位线平行于三角形的第三边，并且等于第三边的一半；

已知：如图，D、E分别是 $△ A B C$ 的边 $A B$ ， $A C$ 中点．

求证： $D E ∥ B C$ ， $D E = \frac{1}{2} B C$ ．

下面是证明的两种添加辅助线的方法，请选择其中一种，完成证明．

方法一

证明：如图，延长 $D E$ 至F ，使 $E F = D E$ ，连接 $C F$ 、 $C D$ 、 $A F$ ．

方法二

证明：如图，过E作 $E F ∥ A B$ 交 $B C$ 于F ，过A作 $A M ∥ B C$ 交 $F E$ 于M ．

查看试题解析

22. 某水果店用1350元购进一批车厘子，受到消费者的欢迎，于是又用了2450元购进第二批，由于第二批的采购量是第一批的2倍，所以比第一批车厘子每斤的进价便宜了5元．

(1)、求第一批和第二批车厘子的进价分别为每斤多少元；

(2)、在销售过程中，水果店以每斤80元的价格销售完了第一批车厘子和第二批车厘子的 $\frac{3}{5}$ ，为了回流资金，决定降价销售余下的车厘子，若两批车厘子的总利润不低于1800元，求降价后的车厘子售价每斤至少多少元；

查看试题解析
23. 在□ABCD中，点O是对角线BD的中点，点E在边BC上，EO的延长线与边AD交于点F ，连接BF、DE如图1．

(1)、求证：四边形BEDF是平行四边形；

(2)、若DE＝DC ， ∠CBD＝45°，过点C作DE的垂线，与DE、BD、BF分别交于点G、H、P如图2．
①当CD＝6．CE＝4时，求BE的长；
②求证：CD＝CH ．

查看试题解析