广东省梅州市大埔县2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 新冠病毒的直径约为120纳米，120纳米 $= 120 \times 0.000001$ 毫米 $= 0.00012$ 毫米，用科学记数法表示为（）

A、 $120 \times 1 0^{- 6}$ 毫米 B、 $1.2 \times 1 0^{- 6}$ 毫米 C、 $12 \times 1 0^{- 7}$ 毫米 D、 $1.2 \times 1 0^{- 4}$ 毫米

查看试题解析
3. 计算 ${(\frac{1}{3})}^{- 2}$ 的结果是（）

A、﹣9 B、9 C、 $\frac{1}{9}$ D、－ $\frac{1}{9}$

查看试题解析
4. 劳动课上，小莉要用三根木棒首尾相接钉一个三角形框架，现有两根木棒长分别为4cm，5cm，则第三根木棒的长可取（）

A、1cm B、4cm C、9cm D、10cm

查看试题解析
5. 下列计算正确的是（）

A、-m•（-m）²＝-m³ B、x⁸÷x²＝x⁴ C、（3x）²＝6x² D、（-a²）³＝a⁶

查看试题解析
6. 下列事件中是确定事件的为（）

A、三角形的内角和是 $180 °$ B、打开电视机正在播放动画片 C、车辆随机经过一个路口，遇到绿灯 D、掷一枚均匀的骰子，掷出的点数是奇数

查看试题解析
7. 如图是用七巧板拼成的正方形桌面，一个小球在桌面上自由地滚动，它最终停在黑色区域的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{8}$ C、 $\frac{3}{16}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图，已知∠A＝∠C＝90°，AB和CD相交于点E．现要添加一个条件，使得 $△ A D E ≌ △ C B E$ 则下列条件中不符合要求的是（）

A、∠ADE＝∠CBE B、AD＝BC C、AE＝CE D、∠EDB＝∠EBD

查看试题解析
9. 骑行是一种健康自然的运动旅游方式，长期坚持骑自行车可增强心血管功能，提高人体新陈代谢和免疫力．如图是骑行爱好者小李某日骑自行车行驶路程（km）与时间（h）的图象，观察图象得到下列信息，其中正确的是（）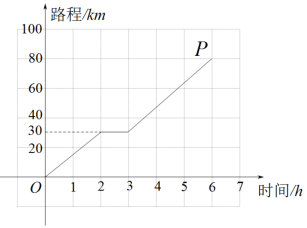

A、小李实际骑行时间为6h B、点P表示出发6h，小李共骑行80km C、3－6h小李的骑行速度比0－2h慢 D、3h内，小李的平均速度是15km/h

查看试题解析
10. 如图，在△ABC中，AB＝AC，按如下步骤作图：以点A为圆心、适当长度为半径作弧，分别交AB、AC于点M、N；分别以点M、N为圆心、大于 $\frac{1}{2}$ MN的长为半径作弧，两弧相交于点F，连接AF并延长，交BC于点E．下列结论不一定成立的是（）

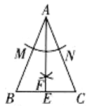A、∠ABC＝∠ACB B、BE＝CE C、AE⊥BC D、∠BAE＝ $\frac{1}{2}$ ∠B

查看试题解析

二、填空题

11. 计算： $1 0^{2} \div 1 0^{0} \times 1 0^{- 2} =$ ．

查看试题解析
12. 如图所示， $a ∥ b$ ， $∠ 1 = 130 °$ ，则 $∠ 2 =$ $°$ ．

查看试题解析
13. 小明抛掷一枚质地均匀的硬币，连续抛掷9次，7次正面朝上，则他抛掷第10次时，正面朝上的概率是．

查看试题解析
14. 若长方形的周长为16，长为y，宽为x，则y与x的关系式为．

查看试题解析
15. 如图，将一个长方形ABCD沿着AE折叠使点D落在BC边上的点F处．如果∠EFC＝50°，则∠DAE的度数是．

查看试题解析

三、解答题

16. 计算下列各式

(1)、 $(- 3)^{2} + (π - 3)^{0} - | - 5 | + (1 - 2)^{2023}$

(2)、 $(x + 2 y) (x - 2 y) + 3 y^{2}$ ；

查看试题解析
17. 先化简，再求值： $[(4 a + b) (b - a) + (2 a - b)^{2}] \div (- b)$ ，其中 $a = - 2$ ， $b = 1$ ．

查看试题解析
18. 一个不透明的袋中装有6个球，分别标有数字3，4，5，6，7，9，每个球除数字外都相同．

(1)、从袋中任意摸出一球，球上的数字不小于5的概率是多少？

(2)、现有两张卡片，分别标有数字3和6．从袋中任意摸出一球，记下数字，与两张卡片上的数字分别作为三条线段的长度．这三条线段能构成三角形的概率是，能构成等腰三角形的概率是．

查看试题解析
19. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上．

⑴在图中画出与 $△ A B C$ 关于直线l成轴对称的 $△ A B^{'} C^{'}$ ；

⑵ $△ A B C$ 的面积为多少？

⑶在直线l上找一点P，使 $P B + P C$ 的长最短．（保留作图痕迹，并写出简单作法）

查看试题解析
20. 请把下面证明过程补充完整：
已知：如图， $∠ A D C = ∠ A B C$ ， $B E$ 、 $D F$ 分别平分 $∠ A B C$ 、 $∠ A D C$ ，且 $∠ 1 = ∠ 2$ ．求证： $∠ A = ∠ C$ ．

证明：∵ $B E$ 、 $D F$ 分别平分 $∠ A B C$ 、 $∠ A D C$ ，

∴ $∠ 1 = \frac{1}{2} ∠ A B C$ ， $∠ 3 = \frac{1}{2} ∠ A D C$ （）．

∵ $∠ A B C = ∠ A D C$ ，

∴ $∠ 1 = ∠ 3$ ，

又∵ $∠ 1 = ∠ 2$ ，

∴ $∠ 2 = ∠ 3$ （）．

∴ ▲ $∥$ ▲ （）．

∴ $∠ A + ∠$ ▲ $= 180 °$ ， $∠ C + ∠$ ▲ $= 180 °$ ．

∴ $∠ A = ∠ C$ （）．

查看试题解析
21. 如图，在△ABC中，GD＝DC，过点G作FG∥BC交BD的延长线于点F，交AB于点E．

(1)、△DFG与△DBC全等吗？说明理由；

(2)、当∠C＝90°，DE⊥BD，CD＝2时，求点D到AB边的距离．

查看试题解析
22. 图①长方形ABCD，AB＝20cm，BC＝16cm，点P从点A出发，沿A－B－C－D的路线以每秒2cm的速度匀速运动，到达点D时停止运动．图②是点P出发x秒时， $△ A P D$ 的面积 $S (c m^{2})$ 与时间 $x (s)$ 的关系图象．

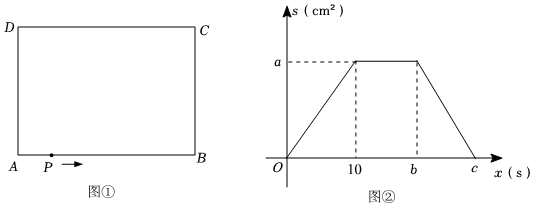(1)、根据题目提供的信息，求出a，b，c的值；

(2)、写出点P距离点D的路程y（cm）与时间x（s）的关系式：

(3)、点P出发几秒时，△APD的面积是长方形ABCD面积的 $\frac{1}{5}$ ？

查看试题解析
23. 有公共顶点的等腰直角三角形 $A C B$ 与等腰直角三角形 $A D E$ 按如图①所示放置， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ，点 $D$ 在 $A C$ 上，点 $E$ 在 $B A$ 的延长线上．连接 $B D$ ， $C E$ ．

(1)、【观察猜想】
$B D$ 与 $C E$ 之间的数量关系是；位置关系是．

(2)、【探究证明】
将等腰直角三角形 $A D E$ 绕点 $A$ 逆时针旋转，如图②所示，使点 $C$ ， $D$ ， $E$ 在同一条直线上，连接 $B D$ ，交 $A C$ 于点 $H$ ． $B D$ 与 $C E$ 之间的关系是否仍然成立？请说明理由

查看试题解析