广东省梅州市梅县区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. “柳条初弄绿，已觉春风驻”.每到春天，人们在欣赏柳绿桃红的同时，也被飞舞的柳絮所烦恼，据了解柳絮纤维的直径约为0.00105cm，则0.00105用科学记数法可表示为（）

A、 $- 1.05 \times 10^{3}$ B、 $1.05 \times 10^{- 3}$ C、 $1.05 \times 10^{- 4}$ D、 $105 \times 10^{- 5}$

查看试题解析
3. 下列长度的三条线段能组成三角形的是（　　）

A、3cm ， 5cm ， 7cm B、3cm ， 3cm ， 7cm C、4cm ， 4cm ， 8cm D、4cm ， 5cm ， 9cm

查看试题解析
4. 下列运算正确的是（）

A、a²•a³=a⁶ B、（a²）³=a⁵ C、（2a）²=4a² D、3a²÷a²=3a

查看试题解析
5. 下列运算中，不能用平方差公式运算的是（）

A、 $(- b - c) (- b + c)$ B、 $- (x + y) (- x - y)$ C、 $(x + y) (x - y)$ D、 $(x + y) (2 x - 2 y)$

查看试题解析
6. “翻开人教版《数学》九年级上册课本恰好翻到第 $56$ 页”这个事件是（）

A、随机事件 B、确定事件 C、不可能事件 D、必然事件

查看试题解析
7. 如图，下列不能判定DF∥AC的条件是（）

A、∠A＝∠BDF B、∠2＝∠4 C、∠1＝∠3 D、∠A+∠ADF＝180°

查看试题解析
8. 已知直线a∥b，将一块含30°角的直角三角板（∠BAC＝30°）按如图所示方式放置，并且顶点A，C分别落在直线a，b上，若∠1＝22°，则∠2的度数是（）

A、38° B、45° C、58° D、60°

查看试题解析
9. 如图，是一台自动测温记录仪的图像，它反映了我市某天气温（℃）随时间（时）变化而变化的关系，观察图像得到下列信息，其中错误的是（）

A、凌晨3时气温最低为16℃ B、14时气温最高为28℃ C、从0时至14时，气温随时间的推移而上升 D、从14时至24时，气温随时间的推移而下降

查看试题解析
10. 一个寻宝游戏通道如图所示，通道在同一平面内由AB、BC、CD、DA、AC、BD组成．定位仪器放置在BC的中点M处，设寻宝者行进时间为x，寻宝者与定位仪器之间的距离为y，寻宝者匀速前进，y与x的函数关系图象如图所示，则寻宝者的行进路线可能是（）

A、A→B→O B、A→D→O C、A→O→D D、B→O→C

查看试题解析

二、填空题

11. 计算： $3 x - (2 x - y) =$ ．

查看试题解析
12. 一个角比它的补角的2倍还少60°，则这个角的度数为度．

查看试题解析
13. 如图，已知AB=CB，要使四边形ABCD成为一个轴对称图形，还需添加一个条件，你添加的条件是．（只需写一个，不添加辅助线）

查看试题解析
14. 张大妈购进一批柚子，在集贸市场零售，已知卖出的柚子重量x（kg）与售价y（元）之间的关系如下表：

重量/kg

1

2

3

…

售价/元

1.2+0.1

2.4+0.1

3.6+0.1

…

根据表中数据可知，若卖出柚子10kg，则售价为元．

查看试题解析
15. 已知 $x - y = 3$ ， $x y = 10$ ，则 ${(x + y)}^{2} =$ ．

查看试题解析
16. 如图，直线l₁∥l₂ ，点A在直线l₁上，点B在直线l₂上，AB＝BC，∠C＝30°，∠1＝80°，则∠2＝．

查看试题解析
17. 如图， $A B ∥ C D$ ， $∠ C = 60 °$ ，点 $E$ 是射线 $C D$ 上一点，连接 $A E$ ，将 $△ A E C$ 沿着 $A E$ 翻折得 $△ A E F$ ，点 $C$ 的对应点为点 $F$ ，若 $∠ E A F = 2 ∠ F A B$ ，那么 $∠ A E C =$ ．

查看试题解析

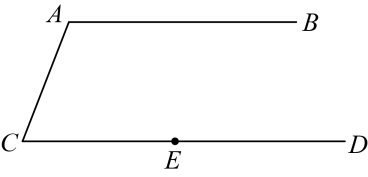
三、解答题

18. 计算： $- 1^{2022} + {(202 2^{2} - 2022)}^{0} - (- 2022)^{- 1}$ ．

查看试题解析
19. 先化简后求值 $[(a - 2 b)^{2} - (2 b + a) (2 b - a)] \div \frac{1}{2} a$ ，其中 $a = 1$ ， $b = - \frac{1}{2}$ ．

查看试题解析
20. 如图，EF//AD，∠1＝∠2，∠BAC＝82°，请将求∠AGD的过程填写完整．
解：因为EF//AD

所以∠2＝∠　 ▲ 　（　   　）

又因为∠1＝∠2

所以∠1＝∠3（　   　）

所以AB//　 ▲ 　（　   　）

所以∠BAC+∠　 ▲ 　＝180°（　   　）

因为∠BAC＝82°

所以∠AGD＝　 ▲ 　°

查看试题解析
21. 如图， $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 15$ ，面积为150

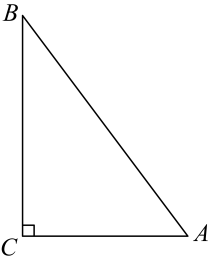(1)、尺规作图：作 $∠ C$ 的平分线交 $A B$ 于点D；（不要求写作法，保留作图痕迹）

(2)、在（1）的条件下，求出点D到两条直角边的距离．

查看试题解析
22. 一个不透明袋中有红、黄、绿三种颜色的球共45个，它们除颜色外都相同，其中黄球个数是绿球个数的2倍．已知从袋中摸出一个球是红球的概率是 $\frac{1}{3}$ ．

(1)、求绿球的个数；

(2)、若从袋中取走5个黄球后，求从袋中随机摸出一个球是黄球的概率．

查看试题解析
23. 如图，在△ABC中，AB＝AC＝2，∠B＝40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE与AC交于E．

(1)、当∠BDA＝115°时，∠BAD＝°，∠DEC＝°；当点D从B向C运动时，∠BDA逐渐变（填”大”或”小”）；

(2)、当DC＝AB＝2时，△ABD与△DCE是否全等？请说明理由：

(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数；若不可以，请说明理由．

查看试题解析
24. 如图，在△ABC中，AB=AC=8，BC=12，点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动，点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动，连接AD、DE，设D、E两点运动时间为t秒（0<t<4）

(1)、运动秒时，AE= $\frac{1}{3}$ DC；

(2)、运动多少秒时，△ABD≌△DCE能成立，并说明理由；

(3)、若△ABD≌△DCE，∠BAC=α，则∠ADE=（用含α的式子表示）．

查看试题解析
25. 如图1，在边长为 $10 c m$ 的正方形 $A B C D$ 中，点P从点A出发，沿A→B→C→D路线运动，到点D停止；点Q从点D出发，沿D→C→B→A路线运动，到点A停止．若点P、点Q同时出发，点P的速度为每秒 $1 c m$ ，点Q的速度为每秒 $2 c m$ ， a秒时点P、点Q同时改变速度，点P的速度为每秒 $2 c m$ ，点Q的速度为每秒 $1 c m$ ，图2是点P出发x秒后 $△ A P D$ 的面积 $S (c m^{2})$ 与 $x (s)$ 关系的图象．

(1)、根据图象得 $a =$ ；

(2)、设点P已行的路程为 $y_{1} (c m)$ ，点Q还剩的路程为 $y_{2} (c m)$ ，试分别求出改变速度后，y₁ ， y₂和出发后的运动时间x（秒）的关系式；

(3)、若点P、点Q在运动路线上相距的路程为 $18 c m$ ，求x的值．

查看试题解析

重量/kg	1	2	3	…
售价/元	1.2+0.1	2.4+0.1	3.6+0.1	…