广东省梅州市兴宁市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 以下分别是回收、节水、绿色包装、低碳4个标志，其中是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 已知a<b，则下列不等式一定成立的是（）

A、 $a + 3 > b + 3$ B、 $2 a > 2 b$ C、 $- a < - b$ D、 $a - b < 0$

查看试题解析
3. 下列各式因式分解正确的是（）

A、x²＋3xy＋9y²＝（x＋3y）² B、2x²-4xy＋9y²＝（2x-3y）² C、x（x-y）＋y（y-x）＝（x-y）（x＋y） D、2x²-8y²＝2（x＋2y）（x-2y）

查看试题解析
4. 在平面直角坐标系内，把点P（-2，4）沿x轴方向向右平移一个单位，则得到的对应点P′的坐标是（）

A、（-1，4） B、（-2，5） C、（-3，4） D、（-2，3）

查看试题解析
5. 把分式 $\frac{x}{x + y}$ （x≠0，y≠0）中的分子、分母的x、y同时扩大为原来的2倍，那么分式的值（）

A、扩大为原来的2倍 B、扩大为原来的4倍 C、缩小为原来的 $\frac{1}{2}$ D、不改变

查看试题解析
6. 如图，AD是等边三角形ABC的中线，点E在AC上，AE＝AD，则∠EDC等于（）

A、15° B、20° C、25° D、30°

查看试题解析
7. 某家具厂要在开学前赶制540套桌凳，为了尽快完成任务，厂领导合理调配，加强第一线人力，使每天完成的桌凳比原计划多2套，结果提前3天完成任务.问原计划每天完成多少套桌凳？设原计划每天完成 $x$ 套桌凳，则所列方程正确的是（）

A、 $\frac{540}{x - 2} - \frac{540}{x} = 3$ B、 $\frac{540}{x + 2} - \frac{540}{x} = 3$ C、 $\frac{540}{x} - \frac{540}{x + 2} = 3$ D、 $\frac{540}{x} - \frac{540}{x - 2} = 3$

查看试题解析
8. 已知m²-n²=mn，则 $\frac{n}{m} - \frac{m}{n}$ 的值等于（）

A、1 B、0 C、-1 D、- $\frac{1}{4}$

查看试题解析
9. 等腰三角形的一个角是80°，则它的顶角的度数是（）

A、80° B、80°或20° C、80°或50° D、20°

查看试题解析
10. 如图，已知△ABC是边长为3的等边三角形，点D是边BC上的一点，且BD＝1，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则下列结论中①△ABD≌△BCF；②四边形BDEF是平行四边形；③S_{四边形BDEF}＝ $\frac{\sqrt{3}}{2}$ ；④S_△_AEF＝ $\sqrt{3}$ .其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解： $a b^{2} - 25 a$ ＝．

查看试题解析
12. 要使分式 $\frac{1}{x + 2}$ 有意义，x的取值应满足的条件是．

查看试题解析
13. 我们定义一种新运算： $x \otimes y = \frac{x y}{3} - 2 y$ ，如 $2 \otimes 3 = \frac{2 \times 3}{3} - 2 \times 3 = - 4$ ，则关于a的不等式 $2 \otimes a \leq 2$ 的最小整数解为．

查看试题解析
14. 一个多边形所有内角都是135°，则这个多边形的边数为．

查看试题解析
15. 如图，在平面直角坐标系xOy中， $△$ ABC的顶点B，C的坐标分别为(- $\sqrt{2}$ ， 0)，(2 $\sqrt{2}$ ， 0)，点A在y轴上，点D为AC的中点，DE⊥AB于点E，若∠ABD＝∠DBC，则DE＝．

查看试题解析

三、解答题

16. 分解因式： $a^{3} + 10 a^{2} + 25 a$ ；

查看试题解析
17. 解不等式组： ${\begin{array}{l} 5 x - 6 \leq 2 (x + 3) \\ 3 - \frac{5 x}{4} < \frac{3 x}{4} - 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
18. 先化简，再求值： $(1 - \frac{4}{x + 3}) \div \frac{x^{2} - 1}{x^{2} + 6 x + 9}$ ，其中 $x = - 4$ .

查看试题解析
19. 如图，在平行四边形 $A B C D$ 中，点H是边 $A B$ 上一点，连接 $C H$ ．

(1)、尺规作图：请作出 $∠ A D C$ 的角平分线，分别交 $C H 、 C B$ 于点G、E，交 $A B$ 的延长线于点F．（不写作法，保留作图痕迹）

(2)、若点G恰好是线段 $C H$ 的中点，求证： $B F = A H$ ．

查看试题解析
20. 如图，ABCD是平行四边形，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA.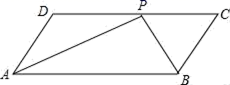

(1)、求∠APB的度数；

(2)、如果AD＝5cm，AP＝8cm，求△APB的周长.

查看试题解析
21. 某商店计划今年的圣诞节购进A、B两种纪念品若干件．若花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的 $\frac{3}{4}$ ，已知每件A种纪念品比每件B种纪念品多4元．

(1)、求购买一件A种纪念品、一件B种纪念品各需多少元？

(2)、若商店一次性购买A、B纪念品共200件，要使总费用不超过3000元，最少要购买多少件B种纪念品？

查看试题解析
22. 我们新定义一种三角形：两边平方和等于第三边平方的 $3$ 倍的三角形叫做非凡三角形．例如：某三角形三边长分别是 $\sqrt{3} ， 2$ 和 $3$ ，因为 ${(\sqrt{3})}^{2} + 3^{2} = 12 = 3 \times 2^{2}$ ，所以这个三角形是非凡三角形．

(1)、判断：等腰直角三角形非凡三角形（填“是”或“不是”)﹔

(2)、若 $△ A B C$ 是非凡三角形，且 $A B = 3 ， B C = 6$ ，则 $A C =$

(3)、如图，在平行四边形 $A B C D$ 中， $A C ⊥ B D$ 于点 $O ， A B = 6$ ，且 $△ A B D$ 是非凡三角形，求 $A C$ 的值．

查看试题解析
23. 如图1，点C、D是线段AB同侧两点，且AC＝BD，∠CAB＝∠DBA，连接BC，AD交于点E.

(1)、求证：AE＝BE；

(2)、如图2，△ABF与△ABD关于直线AB对称，连接EF.
①判断四边形ACBF的形状，并说明理由；

②若∠DAB＝30°，AE＝5，DE＝3，求线段EF的长.

查看试题解析