广东省梅州市兴宁市2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
1. 下列手机中的图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 华为手机使用了自主研发的海思麒麟芯片,目前最新的型号是麒麟990.芯片是由很多晶体管组成的,而芯片技术追求是体积更小的晶体管,以便获得更小的芯片和更低的电力功耗,而麒麟990的晶体管栅极的宽度达到了 毫米,将数据 用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若三角形两边 a、b的长分别为 3 和 4,则第三边c的取值范围是( )A、1≤c≤7 B、1<c<8 C、1<c<7 D、2<c<95. 如图,将木条 , 与钉在一起, , , 要使木条与平行,木条旋转的度数至少是( )
2. 华为手机使用了自主研发的海思麒麟芯片,目前最新的型号是麒麟990.芯片是由很多晶体管组成的,而芯片技术追求是体积更小的晶体管,以便获得更小的芯片和更低的电力功耗,而麒麟990的晶体管栅极的宽度达到了 毫米,将数据 用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若三角形两边 a、b的长分别为 3 和 4,则第三边c的取值范围是( )A、1≤c≤7 B、1<c<8 C、1<c<7 D、2<c<95. 如图,将木条 , 与钉在一起, , , 要使木条与平行,木条旋转的度数至少是( ) A、 B、 C、 D、6. 下列成语,是必然事件的是( )A、画饼充饥 B、不期而遇 C、水中捞月 D、旭日东升7. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )
A、 B、 C、 D、6. 下列成语,是必然事件的是( )A、画饼充饥 B、不期而遇 C、水中捞月 D、旭日东升7. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )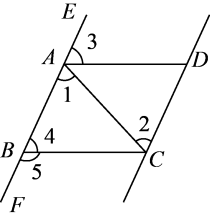 A、①②③ B、①②④ C、①③④ D、②③④8. 如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A、①②③ B、①②④ C、①③④ D、②③④8. 如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( ) A、45° B、65° C、75° D、85°9. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )
A、45° B、65° C、75° D、85°9. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )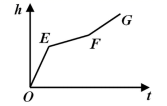 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在中,以点为圆心,为半径画弧交于点 , 以点为圆心,为半径画弧交于点 , 连接 , . 设 , , 则的度数为( )
10. 如图,在中,以点为圆心,为半径画弧交于点 , 以点为圆心,为半径画弧交于点 , 连接 , . 设 , , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°,∠2= .
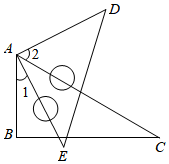 12. 奥园路口红绿灯的时间设置为:红灯90秒,绿灯30秒,黄灯5秒.当人或车随意经过该路口时,遇到红灯的概率是 .13. 如下图,已知 , 要使 . 则需添加一个条件 .
12. 奥园路口红绿灯的时间设置为:红灯90秒,绿灯30秒,黄灯5秒.当人或车随意经过该路口时,遇到红灯的概率是 .13. 如下图,已知 , 要使 . 则需添加一个条件 .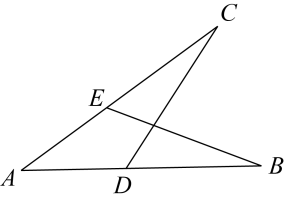 14. 变量x与y之间的关系是 , 当自变量x=2时,因变量y的值是.15. 如图,点P为三边垂直平分线的交点,若 , , 则的度数为 .
14. 变量x与y之间的关系是 , 当自变量x=2时,因变量y的值是.15. 如图,点P为三边垂直平分线的交点,若 , , 则的度数为 . 16.
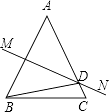
16.如图,△ABC中AB=AC,AB的垂直平分线MN交AC于点D.若AC+BC=10cm,则△DBC的周长为 .
 17. 如图,四边形均为正方形,其中正方形面积为 . 图中阴影部分面积为 , 正方形面积为 .
17. 如图,四边形均为正方形,其中正方形面积为 . 图中阴影部分面积为 , 正方形面积为 .
三、解答题
-
18. 计算:(1)、;(2)、 .19. 先化简,再求值: , 其中a=−1,b= .20. 一起感悟读书之美,推广全民阅读,建设“书香中国”,犹如点亮一座灯塔,撒播一抔种子、开凿一眼清泉.如今,全民阅读已蔚然成风,氤氲书香正飘满中国,听总书记分享他的读书故事,一起感语读书之美,不负韶华梦,读书正当时!某校对A.《三国演义》、B.《红楼梦》、C.《西游记》、D.《水浒传》四大名著开展“传统文化经典著作”推荐阅读活动.(1)、小云从这4部名著中,随机选择1部阅读,他选中《红楼梦》的概率为 .(2)、该校拟从这4部名著中,选择2部作为课外阅读书籍.求《红楼梦》被选中的概率.21. 如图,在直角坐标系中, , , .
 (1)、在图中作出关于轴对称的图形;(2)、写出点 , , 的坐标;(3)、求的面积.22. 如图,点在上,已知 , 平分 , 平分 . 请说明的理由.
(1)、在图中作出关于轴对称的图形;(2)、写出点 , , 的坐标;(3)、求的面积.22. 如图,点在上,已知 , 平分 , 平分 . 请说明的理由.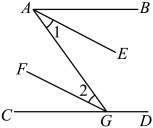
解:因为(已知),
( ),
所以( ).
因为平分 ,
所以( ).
因为平分 ,
所以 ▲ ,
得(等量代换),
所以 ▲ ( ).
23. 综合与实践:有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分钟的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图像,回答下列问题: (1)、A、B两点之间的距离是米,甲机器人前2分钟的速度为米/分;(2)、已知线段轴,前3分钟甲机器人的速度不变.
(1)、A、B两点之间的距离是米,甲机器人前2分钟的速度为米/分;(2)、已知线段轴,前3分钟甲机器人的速度不变.①在3~4分钟的这段时间,甲机器人的速度为 ▲ 米/分.
②请直接写出在整个运动过程中,两机器人相距时x的值.
24. 如图 (1)、如图1,已知中,90°, , 直线经过点直线 , 直线 , 垂足分别为点 . 求证: .(2)、如图2,将(1)中的条件改为:在中,三点都在直线上,并且有 . 请写出三条线段的数量关系,并说明理由.25. 阅读理解,自主探究:
(1)、如图1,已知中,90°, , 直线经过点直线 , 直线 , 垂足分别为点 . 求证: .(2)、如图2,将(1)中的条件改为:在中,三点都在直线上,并且有 . 请写出三条线段的数量关系,并说明理由.25. 阅读理解,自主探究:“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角角度为90°,于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时,则模型中必定存在全等三角形.
 (1)、问题解决:如图1,在等腰直角中, , , 过点C作直线 , 于D,于E,求证:;(2)、问题探究:如图2,在等腰直角中, , , 过点C作直线 , 于D,于E,cm,cm,求的长;(3)、拓展延伸:如图3,在平面直角坐标系中, , 为等腰直角三角形, , , 求B点坐标.
(1)、问题解决:如图1,在等腰直角中, , , 过点C作直线 , 于D,于E,求证:;(2)、问题探究:如图2,在等腰直角中, , , 过点C作直线 , 于D,于E,cm,cm,求的长;(3)、拓展延伸:如图3,在平面直角坐标系中, , 为等腰直角三角形, , , 求B点坐标.