广东省湛江市麻章区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 若使二次根式 $\sqrt{x - 3}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \leq 3$ B、 $x \geq 3$ C、 $x \neq 3$ D、 $x > 3$

查看试题解析
2. 有一组数据：2，5，3，7，5，这组数据的中位数是（）

A、2 B、3 C、5 D、7

查看试题解析
3. 下列计算中，正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{4} \times \sqrt{3} = 2 \sqrt{3}$ D、 $\sqrt{6} \div \sqrt{3} = 2$

查看试题解析
4. 点A（1，m）在y=2x的图象上，则m的值是（）

A、1 B、2 C、 $\frac{1}{2}$ D、0

查看试题解析
5. 如图，平行四边形 $A B C D$ 中， $C E ⊥ A B$ 于E，若 $∠ A = 125 °$ ，则 $∠ B C E$ 的度数为（）

A、 $35 °$ B、 $55 °$ C、 $25 °$ D、 $30 °$

查看试题解析
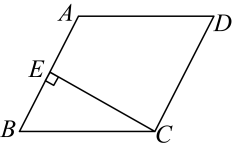6. 如图，数轴上点A所表示的数为a，则a的值是（）

A、2.2 B、2.3 C、 $\sqrt{6}$ D、 $\sqrt{5}$

查看试题解析
7. 下列各组数，可以作为直角三角形的三边长的是（）

A、3，4，6 B、5，12，13 C、8 ，12，20 D、 $\sqrt{3} ， \sqrt{5} ， 2$

查看试题解析
8. 一次函数 $y = 3 x + 2$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 如图，在菱形 $A B C D$ 中， $A C$ 与 $B D$ 交于点O， $A B = 10 ， O B = 6$ ，则菱形 $A B C D$ 的面积为（）

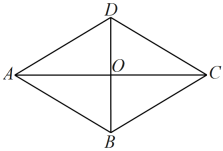A、48 B、96 C、120 D、192

查看试题解析
10.
由四个全等的直角三角形拼成如图所示的“赵爽弦图”，若直角三角形斜边长为2，最短的之边长为1，则图中阴影部分的面积为（　　）

A、1 B、3 C、4﹣2 $\sqrt{3}$ D、4+2 $\sqrt{3}$

查看试题解析

二、填空题

11. 计算：( $- \sqrt{5}$ )²=。

查看试题解析
12. 某学生数学的平时成绩、期中考试成绩、期末考试成绩分别是：85分、80分、90分．如果按平时成绩：期中考试成绩：期末考试成绩 $= 3 ： 3 ： 4$ 进行总评，那么他本学期数学总评分应为分．

查看试题解析
13. 如图， $△ A B C$ 中，D，E分别是 $A C ， B C$ 的中点，若 $A B = 6$ ，则 $D E =$ ．

查看试题解析
14. 如图，函数y=ax和y=bx+c的图象相交于点A（1，2），则不等式ax＞bx+c的解集为．

查看试题解析
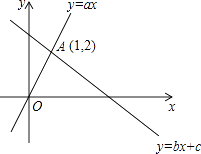15. 如图1，在矩形 $A B C D$ 中，动点P从点B出发，沿 $B C$ 、 $C D$ 、 $D A$ 运动至点A停止，设点P运动的路程为 $x$ ， $△ A B P$ 的面积为 $y$ ，如果 $y$ 关于 $x$ 的函数图象如图2所示，则矩形 $A B C D$ 的周长是．

查看试题解析

三、解答题

16. 计算： $\sqrt{12} - \sqrt{6} \div \sqrt{2} + (\sqrt{3} + 1) (\sqrt{3} - 1)$

查看试题解析
17. 如图，E、F分别是矩形ABCD的边BC、AD上的点，且BE＝DF．求证：四边形AECF是平行四边形．

查看试题解析
18. 如图，四边形ABCD中．若∠B＝90°，AB＝20，BC＝15，CD＝7．AD＝24，先判断∠D是否是直角，再说明理由．

查看试题解析
19. 这三年来，全国上下众志成城，共同抗疫，口罩成为人们防护防疫的必备武器，珠海某药店有3000枚口罩准备出售，从中随机抽取了一部分口罩，根据它们的价格（单位：元），绘制出如图的统计图，请据相关信息，解答下列问题：

(1)、图①中的m值为；

(2)、统计的这些数据的中位数为元，众数为元；

(3)、根据样本数据，估计这3000枚罩中，价格为1.8元的口罩有多少枚？

查看试题解析
20. 如图，已知一次函数 $y = x - 2$ 的图象与y轴交于点A，一次函数 $y = k x + b$ 的图象与y轴交于点B，且与x轴以及一次函数 $y = x - 2$ 的图象分别交于点 $C (- 1 ， 0) 、 D (- 2 ， m)$ ．

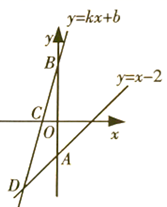(1)、求D点坐标；

(2)、求一次函数 $y = k x + b$ 的函数解析式；

(3)、求 $△ A B D$ 的面积．

查看试题解析
21. 在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $O$ 是AC的中点．求证： $B O = \frac{1}{2} A C$ ．

查看试题解析
22. 某中学为丰富学生的课余生活，准备购买一批每副售价50元的羽毛球拍和每简售价10元的羽毛球. 购买时，发现商场正在进行两种优惠促销活动.
活动甲：买一副羽毛球拍送一筒羽毛球；
活动乙：按购买金额打9折付款.
学校欲购买这种羽毛球拍10副，羽毛球x（x≥.10）筒.

(1)、写出每种优惠办法实际付款金额y_甲（元），y_乙（元）与x（筒）之间的函数关系式.

(2)、比较购买同样多的羽毛球时，按哪种优惠办法付款更省钱？

(3)、如果商场允许可以任意选择一种优惠办法购买，也可以同时用两种优惠办法购买，请你就购买这种羽毛球拍10副和羽毛球60筒设计一种最省钱的购买方案.

查看试题解析
23. 如图1，已知四边形ABCD是正方形，E是对角线BD上的一点，连接AE，CE．

(1)、求证：AE＝CE；

(2)、如图2，点P是边CD上的一点，且PE⊥BD于E，连接BP，O为BP的中点，连接EO．若∠PBC＝30°，求∠POE的度数；

(3)、在（2）的条件下，若OE＝ $\sqrt{2}$ ，求CE的长．

查看试题解析