广东省深圳市盐田区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，木工用角尺画平行线的道理是（）

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、同旁内角相等，两直线平行 D、同旁内角互补，两直线平行

查看试题解析
2. 下列用七巧板拼成的图形（不考虑内部线条）中，为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算的结果为a⁶的是（）

A、 $a^{3} + a^{3}$ B、 ${(a^{3})}^{3}$ C、 $a^{3} \cdot a^{3}$ D、 $a^{12} \div a^{2}$

查看试题解析
4. 一副三角板按如图所示放置，斜边互相平行，且每个三角板的直角顶点都在另一个三角板的斜边上，在图中所标记的角中，与 $∠ 1$ 相等的角是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
5. 下列算式中，正确的是（）

A、 $| 3 - π | = 3 - π$ B、 $- 2^{- 2} = \frac{1}{4}$ C、 $2^{5} \times 0.2 5^{2} = \frac{1}{2}$ D、 $- 2^{0} = - 1$

查看试题解析
6. 下列图形中，能借助其面积“形象”解释平方差公式的是（）

A、 B、 C、 D、

查看试题解析
7. 碳12的原子质量为 $0 . \overset{22 个 0}{\overset{︷}{00 \cdot \cdot \cdot 00}} 1933 g$ ，这个数用科学记数法表示是（）

A、 $1.993 \times 1 0^{- 22}$ B、 $1.993 \times 1 0^{- 23}$ C、 $1.993 \times 1 0^{22}$ D、 $1.993 \times 1 0^{23}$

查看试题解析
8. 佳佳和爸爸一道从家出发，25min后走到离家1000m的公园，爸爸随即原速返回，她停留10min后返回，两人恰好同时到家，下列图象中，表示她离家后距离与时间关系的是（）

A、 B、 C、 D、

查看试题解析
9. 如图， $△ A B C$ 是等边三角形，D，E分别是 $B C ， A C$ 边的中点，连接 $A D$ ，点P是 $A D$ 上一动点，若 $A D = 8$ ，则 $P C + P E$ 的最小值是（）

A、2 B、4 C、8 D、16

查看试题解析
10. 如图， $A B ∥ C D$ ， $A B = B D = 2 C D$ ， $E$ 是 $A B$ 中点．连接 $E D$ ，连接 $C E$ 交 $B D$ 于点 $F$ ，连接 $A F$ 交 $D E$ 于点 $P$ ，作射线 $B P$ 交 $A D$ 于点 $H$ ．给出结论：① $F$ 是 $B D$ 中点；② $∠ B A F = ∠ B D E$ ；③ $B H ⊥ A D$ ；④ $B C ∥ D E$ ，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 如图是某天北京与上海的气温随时间变化的图象，这一天内，两地在时气温相同．

查看试题解析
12. 计算 $(a + b) (b - a) =$ ．

查看试题解析
13. 50件外观相同的产品中有2件不合格，现从中随机抽取1件进行检测，抽到不合格产品的概率是．

查看试题解析
14. 如图， $A B ∥ C D$ ， $∠ G = ∠ F E H = 90 °$ ， $∠ G E F = 45 ° ， ∠ H = 60 °$ ，若 $∠ A E G = 26 °$ ，则 $∠ D F H =$ ．

查看试题解析
15. 如图，直线l为线段 $A B$ 的垂直平分线，垂足为C ，直线l上的两点E ， F位于 $A B$ 异侧（E ， F两点不与点C重合）．只需添加一个条件即可证明 $△ A C E ≌ △ B C F$ ，这个条件可以是．

查看试题解析

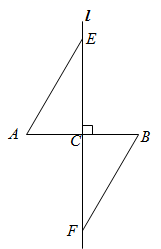
三、解答题

16. 计算：

(1)、 $a^{2} \cdot a^{4} + (2 a^{3})^{2} - 3 a^{7} \div a$ ；

(2)、 $m (2 m - 3) - (m - 4) (m + 1)$ ．

查看试题解析
17. 利用乘法公式计算：

(1)、 $32 5^{2} - 27 5^{2}$ ；

(2)、 $295 \times 305 - 29 8^{2}$ ．

查看试题解析
18. 先化简，再代入求值： $3 (a - b)^{2} + (a - b) (a + b) - (2 a + b)^{2}$ ．其中 $a = \frac{1}{5}$ ， $b = - 2$ ．

查看试题解析
19. 在网格图中，每个方格除颜色外都相同，其中4个方格为黑色，余下方格为白色．

(1)、涂黑3个白色方格，使整个网格图为轴对称图形（考虑颜色）；

(2)、在（1）的轴对称网格图中任取1个方格，恰好是黑色方格的概率是多少？

(3)、在（1）的轴对称网格图中，再涂黑若干个白色方格，能否使任取1个方格恰好是白色方格的概率为0.5？

查看试题解析
20. 已知 $∠ A O B$ ．利用尺规作图：①在 $O A$ 的反向延长线和 $O B$ 上分别截取 $O C ， O D$ ，使 $O C = O D$ ，连接 $C D$ ；②以点C为圆心，任意长为半径作弧，交 $C D$ 于点M，交 $C O$ 于点N；③以点O为圆心， $C M$ 长为半径作弧，交 $O B$ 于点E；④以点E为圆心， $M N$ 长为半径作弧，交前面的弧于点F，连射线 $O F$ ．

根据上述作图步骤填空：

∵ $O C = O D$ ．

∴ $∠ O C D = ∠$     ▲        （）

∵步骤2～4可得： $∠ O C D = ∠$     ▲         ．

∴ $∠ F O E = ∠ O D C$ （）．

∴    ▲         $∥ C D$ （）．

∴ $∠ O C D = ∠$     ▲        （两直线平行，同位角相等）．

∴ $∠$     ▲         $= ∠$     ▲         ．

∴ $O F$ 平分 $∠ A O B$ ．

查看试题解析
21. 佳佳和萌萌一起参加中长跑，起跑后路程 $S (m)$ 与时间 $t (m i n)$ 之间的关系如图所示．

(1)、在上述关系中，自变量是，因变量是；

(2)、这次比赛的路程是m；

(3)、萌萌将本次中长跑分起跑、途中跑和冲刺跑三阶段，经历了两次变速，在第 $m i n$ 速度最慢，速度为 $m / m i n$ ；

(4)、通过计算说明萌萌与佳佳何时相遇．

查看试题解析
22.

(1)、计算：
① $(x + 9) (x + 4)$ ；
② $(x - 2) (x - 18)$ ．

(2)、分别求 $n$ 的值：
① $(x - 3) (x + m) = x^{2} + n x + 36$ ；
② $(x - 6) (x + m) = x^{2} + n x + 36$ ．

(3)、已知 $(x + p) (x + q) = x^{2} + n x + 6$ ， $p$ 、 $q$ 为正整数，求 $n$ 的值．

查看试题解析
23. 定理：三角形任意两边之和大于第三边．

(1)、如图1，线段 $A D$ ， $B C$ 交于点 $E$ ，连接 $A B$ ， $C D$ ，判断 $A D + B C$ 与 $A B + C D$ 的大小关系，并说明理由；

(2)、如图2， $O C$ 平分 $∠ A O B$ ， $P$ 为 $O C$ 上任意一点，在 $O A$ ， $O B$ 上截取 $O E = O F$ ，连接 $P E$ ， $P F$ ．求证： $P E = P F$ ；

(3)、如图3，在 $△ A B C$ 中， $A B > A C$ ， $P$ 为角平分线 $A D$ 上异于端点的一动点，求证： $P B - P C > B D - C D$ ．

查看试题解析