广东省中山市2022-2023学年八年级下学期数学期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 要使 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围为（）

A、 $x \leq 0$ B、 $x ≥ 1$ C、 $x \geq 0$ D、 $x \leq 1$

查看试题解析
2. 下列各式中，属于最简二次根式的是（）

A、 $\sqrt{2}$ B、 $\sqrt{9}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{12}$

查看试题解析
3. 在某次“汉字听写大赛”选拔赛中，甲、乙两位同学 $5$ 轮比赛成绩的平均分都是 $95$ 分，其中甲的成绩方差是 $12$ ，乙的成绩方差是 $4$ ，则下列说法正确的是（）

A、甲、乙的成绩一样稳定 B、甲的成绩比乙的成绩稳定 C、乙的成绩比甲的成绩稳定 D、无法确定甲、乙的成绩谁更稳定

查看试题解析
4. 下列长度的三条线段能组成直角三角形的是（）

A、1，1，2 B、1，2，3 C、1，1， $\sqrt{2}$ D、2，3，4

查看试题解析
5. 如图，在平行四边形 $A B C D$ 中， $∠ A + ∠ C = 120 °$ ，则 $∠ C$ 的度数为（）

A、 $50 °$ B、 $60 °$ C、 $70 °$ D、 $120 °$

查看试题解析
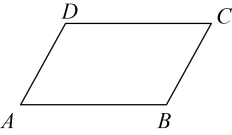6. 下列选项中，矩形一定具有的性质是（）

A、对角线相等 B、对角线互相垂直 C、邻边相等 D、一条对角线平分一组对角

查看试题解析
7. 如图，A，C之间隔有一湖，在与 $A C$ 方向成 $90 °$ 角的 $C B$ 方向上的点B处测得 $A B = 500 m$ ， $B C = 400 m$ ，则AC的长为（）

A、 $300 m$ B、 $400 m$ C、 $500 m$ D、 $600 m$

查看试题解析
8. 对于函数 $y = x + 2$ ，下列说法正确的是（）

A、它的图象经过二、三、四象限 B、它的图象经过 $（ - 1 ， - 1 ）$ C、y随x增大而减小 D、它的图象与y轴的交点为 $(0 ， 2)$

查看试题解析
9. 一次函数 $y = k x + b$ 的图象如图所示，则不等式 $k x + b \leq 0$ 的解集是（）

A、 $x \geq 0$ B、 $x \leq 0$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
10. 如图，在矩形 $O A B C$ 中，点B的坐标是 $（ 5 ， 12 ）$ ，则AC的长是（）

A、5 B、7 C、12 D、13

查看试题解析

二、填空题

11. 计算： $\sqrt{6} \div \sqrt{2} =$ .

查看试题解析
12. 数据 $3$ ， $4$ ， $4$ ， $5$ ， $7$ 的众数是．

查看试题解析
13. 将直线 $y = - 3 x$ 向上平移 $2$ 个单位长度，则平移后的直线解析式为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $∠ A = 28 °$ ， D是 $A C$ 的中点，则 $∠ C B D =$ °．

查看试题解析
15. 《九章算术》勾股卷有一题目：今有垣高六尺，依木于垣，上于垣齐．引木却行二尺，其木至地，问木长几何?意思是：如图，一道墙 $A B$ 高6尺，一根木棒 $A C$ 靠于墙上，木棒上端与墙头齐平．若木棒下端向右滑，则木棒上端会随着往下滑，当木棒下端向右滑2尺到D处时，木棒上端恰好落到地上B处，则木棒长尺．

查看试题解析

三、解答题

16. 计算： $\sqrt{5} \times (\sqrt{20} - \sqrt{45} + 4 \sqrt{5})$ ．

查看试题解析
17. 某校为加强劳动教育，需招聘一位劳动教师．经过对甲、乙两名候选人进行测试，他们的各项测试成绩如下表所示．根据实际需要，学校将笔试、上课、答辩三项测试得分按 $3 ： 5 ： 2$ 的比例来确定个人的综合测试成绩，请判断谁会被录取，并说明理由．
候选人
笔试
上课
答辩
甲
$85$
$83$
$90$
乙
$80$
$84$
$91$

查看试题解析
18. 已知正比例函数 $y = (k - 2) x$ ．

(1)、若它的图象经过第二、四象限，求 $k$ 的取值范围；

(2)、若点 $(2 ， 4)$ 在它的图象上，求它的解析式．

查看试题解析
19. 某校为了解学生一周课外阅读情况，随机抽取部分学生调查了他们一周课外阅读时间，并将数据进行整理制成如下统计图．请根据图中提供的信息，解答以下问题：

(1)、本次调查数据的中位数是；

(2)、抽查的这些学生一周平均的课外阅读时间是多少?

(3)、若该校共有2000个学生，请根据统计数据，估计该校学生一周课外阅读时间不少于3小时的人数．

查看试题解析
20. 某服装厂接到一批任务，需要 $15$ 天内生产出 $800$ 件服装．生产 $5$ 天后，为按期完成任务，该服装厂增加了一定数目的工人，恰好在规定时间内完成任务．设该服装厂生产天数为 $x$ 天，累计生产服装的数量为 $y$ 件，则 $y$ 与 $x$ 之间的关系如图所示．

(1)、求增加工人后 $y$ 与 $x$ 的函数表达式；

(2)、问生产几天后的服装总件数恰好为 $500$ 件?

查看试题解析
21. 如图，在 $△ A B C$ 中，D是 $A B$ 的中点，E是 $B C$ 的中点， $D F ⊥ A C$ 于点F， $E G ⊥ A C$ 于点G．

(1)、求证：四边形 $D E G F$ 为矩形；

(2)、若 $A B = A C = 2 \sqrt{5}$ ， $A F = 1$ ，求矩形 $D E G F$ 的周长．

查看试题解析
22. 如图，已知四边形 $O A B C$ 为菱形，点B在x轴上，过点C的直线 $C D$ 交x轴于点D．其中直线 $C D$ 的解析式为 $y = x + 1$ ，点B的坐标为 $(2 ， 0)$ ，连接 $A C$ 交x轴于点E．

(1)、求 $A C$ 的长；

(2)、点P为x轴下方直线 $C D$ 上一点，若 $△ C O P$ 的面积为菱形 $O A B C$ 的面积一半，求点P的坐标．

查看试题解析
23. 定义“点 $P$ 对图形 $Q$ 的可视度”：在平面直角坐标系中，对于点P和图形 $Q$ ，若图形 $Q$ 上所有的点都在 $∠ P$ 的内部或 $∠ P$ 的边上，则 $∠ P$ 的最小值称为点 $P$ 对图形 $Q$ 的可视度．如图1，点 $O$ 对线段 $A B$ 的可视度为 $∠ A O B$ 的度数．

(1)、如图2，已知点 $A (- 3 ， 1)$ ， $B (2 ， 1)$ ， $C (0 ， 2)$ ， $D (1 ， 3)$ ．连接 $D A$ ， $D B$ ，则 $∠ A D B$ 的度数为点 $D$ 对 $△ A B C$ 的可视度．求证： $∠ A D B = 90 °$ ；

(2)、如图3，已知四边形 $A B C D$ 为正方形，其中点 $A (- 1 ， 1)$ ， $B (- 1 ， - 1)$ ．直线 $y = \frac{\sqrt{3}}{3} x + b$ 与 $x$ 轴交于点 $E$ ，与 $y$ 轴交于点 $F$ ，其中点 $F$ 对正方形 $A B C D$ 的可视度为 $60 °$ ．求点 $E$ 的坐标；

(3)、在（2）的条件下，在平面直角坐标系内是否存在点 $M$ ，使以点 $A$ ， $B$ ， $E$ ， $M$ 为顶点的四边形为平行四边形?若存在，请直接写出点 $M$ 坐标；若不存在，请说明理由．

查看试题解析

候选人	笔试	上课	答辩
甲	$85$	$83$	$90$
乙	$80$	$84$	$91$