浙江省金华市婺城区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，属于二元一次方程的是（）

A、 $x^{2} - y = 1$ B、 $x + \frac{1}{y} = 2$ C、 $x + y = 3 z$ D、 $2 x + 3 y = 4$

查看试题解析
2. “笑脸”图案如图所示，通过平移该图案可以得到的是（）

A、 B、 C、 D、

查看试题解析
3. 互联网已经进入 $5 G$ 时代，应用 $5 G$ 网络下载一个 $100 K B$ 的文件只需要 $0.00076$ 秒，其中数 $0.00076$ 用科学记数法表示为（）

A、 $76 \times 1 0^{- 3}$ B、 $7.6 \times 1 0^{- 3}$ C、 $7.6 \times 1 0^{- 4}$ D、 $7.6 \times 1 0^{- 5}$

查看试题解析
4. 下列计算中，正确的是（）

A、 ${(x^{2} y)}^{3} = x^{6} y^{3}$ B、 $x^{8} \div x^{2} = x^{4}$ C、 $2 x + 3 y = 5 x y$ D、 $x \cdot x^{4} = x^{4}$

查看试题解析
5. 下列从左到右的变形，其中是因式分解的是（）

A、 $2 (a - b) = 2 a - 2 b$ B、 $m^{2} - 1 = (m + 1) (m - 1)$ C、 $x^{2} - 2 x + 1 = x (x - 2) + 1$ D、 $a (a - b) (b + 1) = (a^{2} - a b) (b + 1)$

查看试题解析
6. 已知 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 是关于x，y的二元一次方程x-ay=3的一个解，则a的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
7. 将一个直角三角板和无刻度的直尺按如图所示放置，使三角板的直角顶点放在直尺的一边上，已知 $∠ 1 = 30 °$ ，则 $∠ 2$ 的度数为（）

A、 $60 °$ B、 $50 °$ C、 $45 °$ D、 $30 °$

查看试题解析
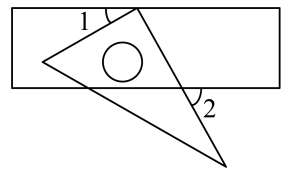8. 如图，10块相同的长方形墙砖拼成一个长方形，设长方形墙砖的长和宽分别为x厘米和y厘米，则依题意列方程组正确的是（）

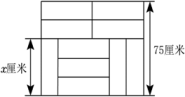A、 ${\begin{array}{l} 2 x + y = 75 \\ y = 3 x \end{array}$ B、 ${\begin{array}{l} 2 x + y = 75 \\ x = 3 y \end{array}$ C、 ${\begin{array}{l} x + 2 y = 75 \\ x = 3 y \end{array}$ D、 ${\begin{array}{l} x + 2 y = 75 \\ y = 3 x \end{array}$

查看试题解析
9. 将矩形纸带按如图所示方式折叠，若 $∠ 1 = 50 °$ ，则 $∠ 2 =$ （）

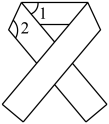A、130° B、125° C、120° D、115°

查看试题解析
10. 若 $p = \frac{1}{n (n + 2)} + \frac{1}{(n + 2) (n + 4)} + \frac{1}{(n + 4) (n + 6)} + \frac{1}{(n + 6) (n + 8)} + \frac{1}{(n + 8) (n + 10)}$ ，则使p最接近 $\frac{1}{10}$ 的正整数n是（　）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 因式分解： $x^{2} - 4 =$ .

查看试题解析
12. 已知 $3^{m} = 5$ ， $3^{n} = 6$ ，则 $3^{m + n} =$ ．

查看试题解析
13. 如果 $a - b +3 = 0$ ，那么代数式 $2 - 3 a + 3 b$ 的值是.

查看试题解析
14. 若 $\frac{x}{y} = \frac{2}{5}$ ，则 $\frac{3 y - 2 x}{3 y + 2 x} =$ ．

查看试题解析
15. 已知关于x，y的方程组 ${\begin{array}{l} x + 2 y = k + 2 \\ 2 x - 3 y = 3 k - 1 \end{array}$ ，无论k取何值， $x + 9 y$ 的值都是一个定值，则这个定值为．

查看试题解析
16. 如果一个自然数M的个位数字不为0，且能分解成 $A \times B$ （ $A \geq B$ ），其中A与B都是两位数，A与B的十位数字相同，个位数字之和为6，则称数M为“如意数”，并把数M分解成 $M = A \times B$ 的过程，称为“快乐分解”．例如，因为 $528 = 22 \times 24$ ， 22和24的十位数字相同，个位数字之和为6，所以528是“如意数”．

(1)、最小的“如意数”是；

(2)、把一个“如意数”M进行“快乐分解”，即 $M = A \times B$ ， A与B的和记为 $P （ M ）$ ， A与B的差记为 $Q （ M ）$ ，若 $\frac{P (M)}{Q (M)}$ 能被7整除，则M的值为．

查看试题解析

三、解答题

17. 计算： ${(- 1)}^{2023} + \sqrt{16} - {(π - 3)}^{0} - 2^{- 1}$ ．

查看试题解析
18. 先化简再求值： $\frac{x - 1}{x - 2} \cdot \frac{x^{2} - 4}{x^{2} - 2 x + 1} - \frac{2}{x - 1}$ ，其中 $x = 2$ ．

查看试题解析
19. 解下列方程（组）：

(1)、 ${\begin{array}{l} x + 2 y = 9 \\ 3 x - 2 y = 3 \end{array}$ ；

(2)、 $\frac{2 - x}{x - 3} + 3 = \frac{2}{3 - x}$ ．

查看试题解析
20. 如图，在 $10 \times 8$ 的正方形网格中，每个小正方形的边长为1，其顶点称为格点，格点 $△ A B C$ 与点D的位置如图所示．

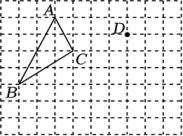(1)、平移格点 $△ A B C$ ，画出平移后的格点 $△ D E F$ （点A，B，C的对应点分别为点D，E，F）．

(2)、连结 $A D$ ， $C F$ ，则线段 $A D$ 与线段 $C F$ 的关系是．

(3)、四边形 $A D F C$ 的面积为．

查看试题解析
21. 为激发学生参与劳动的兴趣，某校开设了以“端午”为主题的活动课程，要求每位学生在“折纸龙”“采艾叶”“做香囊”与“包粽子”四门课程中选且只选其中一门，随机调查了本校部分学生的选课情况，绘制了两幅不完整的统计图.请根据图表信息回答下列问题：

(1)、求本次调查学生的人数，并补全条形统计图．

(2)、求图2中“做香囊”扇形圆心角的度数．

(3)、已知本校共有1000名学生，试估计选择“折纸龙”的学生有多少人？

查看试题解析
22. 如图，用四块完全相同的小长方形拼成一个“回形”正方形．

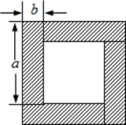(1)、用不同代数式表示图中的阴影部分的面积，可得等式．

(2)、利用（1）中的结论解决下列问题：
①已知 $m + n = 5$ ， $m n = \frac{9}{4}$ ，求 $m - n$ 的值；

②若 ${(x - 2023)}^{2} + {(2009 - x)}^{2} = 130$ ，求 $(x - 2023) (2009 - x)$ 值．

查看试题解析
23. 商场为庆祝母亲节，为了促进消费，推出赠送“优惠券”活动，其中优惠券分为三种类型.如下表：
A型
B型
C型
满368减100
满168减68
满50减20
在此次活动中，小温领到了三种不同类型的“优惠券”若干张，准备给妈妈买礼物.

(1)、若小温同时使用三种不同类型的“优惠券”消费，共优惠了520元，已知她用了1张A型“优惠券”，4张C型“优惠券”，则她用了张B型“优惠券”.

(2)、若小温同时使用了5张A，B型“优惠券”，共优惠了404元，那么他使用了A，B“优惠券”各几张？

(3)、若小温共领到三种不同类型的“优惠券”各16张（部分未使用），他同时使用A，B，C型中的两种不同类型的“优惠券”消费，共优惠了708元，请问有哪几种优惠券使用方案？（请写出具体解题过程）

查看试题解析
24. 数学兴趣小组围绕“三角形的内角和是 $180 °$ ”，进行了一系列探究，过程如下：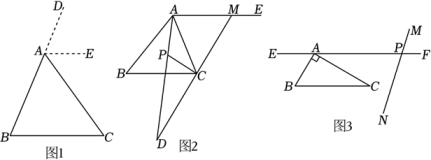

(1)、【论证】如图1，延长 $B A$ 至D，过点 $A$ 作 $A E ∥ B C$ ，就可以说明 $∠ B A C + ∠ B + ∠ C = 180 °$ 成立，即：三角形的内角和为 $180 °$ ，请完成上述说理过程．

(2)、【应用】如图2，在 $△ A B C$ 中， $∠ B A C$ 的平分线与 $∠ A C B$ 的角平分线交于点 $P$ ，过点 $A$ 作 $A E ∥ B C$ ， $M$ 在射线 $A E$ 上，且 $∠ A C M = ∠ A M C$ ， $M C$ 的延长线与 $A P$ 的延长线交于点D．
①求 $∠ D C P$ 的度数；
②设 $∠ B = α$ ，请用 $α$ 的代数式表示 $∠ D$ ．

(3)、【拓展】如图3，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A C B = 30 °$ ，过点A作 $E F ∥ B C$ ，直线 $M N$ 与 $E F$ 相交于A点右侧的点P， $∠ A P N = 75 °$ ． $△ A B C$ 绕点 $A$ 以每秒 $12 °$ 的速度顺时针方向旋转，同时 $M N$ 绕点 $P$ 以每秒 $5 °$ 的速度顺时针方向旋转，与 $E F$ 重合时 $M N$ 再绕着点 $P$ 以原速度逆时针方向旋转，当 $△ A B C$ 旋转一周时，运动全部停止，设运动时间为 $t$ 秒，在旋转过程中，是否某一时刻，使得 $M N$ 与 $△ A B C$ 的一边平行？若存在，求 $t$ 的值；若不存在，请说明理由．

查看试题解析

A型	B型	C型
满368减100	满168减68	满50减20