浙江省金华市婺城区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-17 类型:期末考试
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知关于的一元二次方程有两个相等的实数根,则的值为( )A、2 B、 C、0 D、15. 要判断一个四边形是否为矩形,下面是4位同学拟定的方案,其中正确的是 ( )A、测量两组对边是否分别相等 B、测量两条对角线是否互相垂直平分 C、测量其中三个内角是作都为直角 D、测量两条对角线是否相等6. 用反证法证明“在△ABC中,若∠A>∠B,则a>b“时,应假设( )A、a<b B、a≤b C、a=b D、a≥b7. 已知一组数据1,3,3,5,加入一个数3后,下列各统计量中,会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,在正方形中, , 点、分别是边、的中点,连接、 , 点 , 分别是 , 的中点,则的长为( )
4. 已知关于的一元二次方程有两个相等的实数根,则的值为( )A、2 B、 C、0 D、15. 要判断一个四边形是否为矩形,下面是4位同学拟定的方案,其中正确的是 ( )A、测量两组对边是否分别相等 B、测量两条对角线是否互相垂直平分 C、测量其中三个内角是作都为直角 D、测量两条对角线是否相等6. 用反证法证明“在△ABC中,若∠A>∠B,则a>b“时,应假设( )A、a<b B、a≤b C、a=b D、a≥b7. 已知一组数据1,3,3,5,加入一个数3后,下列各统计量中,会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,在正方形中, , 点、分别是边、的中点,连接、 , 点 , 分别是 , 的中点,则的长为( )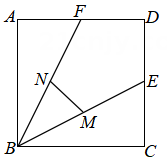 A、 B、 C、 D、29. 对于反比例函数 , 当时,的取值范围是( )A、 B、 C、 D、或10. 如图,在中(), , 对角线交于点 , 动点从点出发,沿着→→运动.设点E运动的路程为 , 的面积为 , 关于的函数图象如图所示.则长为( )
A、 B、 C、 D、29. 对于反比例函数 , 当时,的取值范围是( )A、 B、 C、 D、或10. 如图,在中(), , 对角线交于点 , 动点从点出发,沿着→→运动.设点E运动的路程为 , 的面积为 , 关于的函数图象如图所示.则长为( )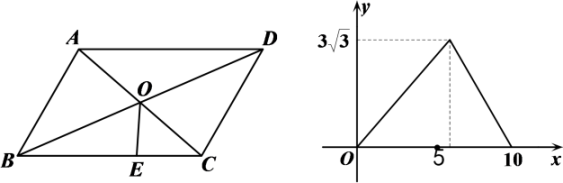 A、5 B、6 C、 D、
A、5 B、6 C、 D、二、填空题
-
11. 当a=2时,二次根式 的值是。12. 过七边形一个顶点可以引出的对角线的条数为 .13. 若一组数据x,3,1,6,3的平均数和众数相等,则x的值为14. 如图,已知的顶点分别在反比例函数和的图象上,且轴.若的面积为3,则 .
 15. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,是矩形的对角线,将分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若 , 则矩形的面积是 .
15. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,是矩形的对角线,将分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若 , 则矩形的面积是 . 16. 如图,在菱形中, , , 将向右平移得到(点在线段上),连接 . 在平移过程中,
16. 如图,在菱形中, , , 将向右平移得到(点在线段上),连接 . 在平移过程中,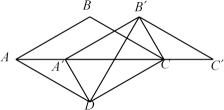 (1)、若四边形是矩形,则;(2)、的最小值为 .
(1)、若四边形是矩形,则;(2)、的最小值为 .三、解答题
-
17. 计算: .18. 解方程:(1)、;(2)、 .19. 图1、图2、图3均为的正方形网格,每个小正方形的顶点称为格点,点均在格点上.请按要求仅用无刻度的直尺作图,保留作图痕迹,不写画法.
 (1)、在图1的网格内作一点 , 使得 , 且;(2)、在图2的网格内作一点 , 使得点为线段的中点;(3)、在图3的网格内作一点 , 满足点在线段上,且平分 .20. 如图,菱形的对角线交于点 , 点是菱形外一点, . 试判定四边形的形状,并给出证明.
(1)、在图1的网格内作一点 , 使得 , 且;(2)、在图2的网格内作一点 , 使得点为线段的中点;(3)、在图3的网格内作一点 , 满足点在线段上,且平分 .20. 如图,菱形的对角线交于点 , 点是菱形外一点, . 试判定四边形的形状,并给出证明. 21. 为了解全校1200名学生假期一周内平均每天在家体育锻炼时间的情况,随机调查了该校100名学生一周内平均每天在家体育锻炼时间的情况,结果如下表,根据信息完成下列问题:
21. 为了解全校1200名学生假期一周内平均每天在家体育锻炼时间的情况,随机调查了该校100名学生一周内平均每天在家体育锻炼时间的情况,结果如下表,根据信息完成下列问题:时间(分)
20
30
40
50
60
人数
34
27
20
13
6
(1)、根据统计表信息,直接写出这100名学生一周内平均每天在家体育锻炼时间的平均数、中位数和众数.(2)、请估计该校一周内平均每天在家体育锻炼时间不少于40分钟的学生大约有多少人?(3)、学校要给学生制定每天的锻炼目标,为了提高学生的锻炼积极性并且使一半以上的学生能达标,如果你是决策者,从平均数、中位数、众数的角度进行分析,你将选择哪个统计量作为“达标标准”,简要说明理由.22. 随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2016年底拥有家庭电动自行车125辆,2018年底家庭电动自行车的拥有量达到180辆.
(1)、若该小区2016年底到2019年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2019年底家庭电动自行车将达到多少辆?(2)、为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.

