【备考2024】高考数学（代数版块）细点逐一突破复习专练：不等式的实际应用

试卷更新日期：2023-08-16 类型：二轮复习

进入出卷网下载

一、选择题

1. 无字证明来源于《几何原本》第二卷的几何代数法（用几何方法研究代数问题），很多代数的公式或定理都能仅通过图形得以证明、如图，在 $△ A B C$ 中， $D ， E$ 为BC边上异于端点的两点， $B D = a ， E C = c$ ，且 $△ A D E$ 是边长为b的正三角形，则下列不等式一定成立的是（）

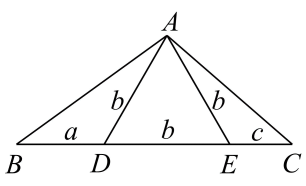A、 $\sqrt{a^{2} + a c + c^{2}} - \sqrt{b^{2} + b c + c^{2}} > a + b + c$ B、 $\sqrt{a^{2} + a b + b^{2}} + \sqrt{b^{2} + b c + c^{2}} > a + b + c$ C、 $\sqrt{a^{2} + a b + b^{2}} - \sqrt{b^{2} - b c + c^{2}} < a + b - c$ D、 $\sqrt{b^{2} + b c + c^{2}} - \sqrt{a^{2} - a b + b^{2}} < a - b + c$

查看试题解析
2. 某学生月考数学成绩 x不低于100分，英语成绩 y 和语文成绩 z 的总成绩高于200分且低于240分，用不等式组表示为（）

A、 ${\begin{matrix} x > 100 \\ 200 < y + z < 240 \end{matrix}$ B、 ${\begin{matrix} x \geq 100 \\ 200 \leq y + z \leq 240 \end{matrix}$ C、 ${\begin{matrix} x > 100 \\ 200 \leq y + z \leq 240 \end{matrix}$ D、 ${\begin{matrix} x \geq 100 \\ 200 < y + z < 240 \end{matrix}$

查看试题解析
3. 某位同学经常会和爸爸妈妈一起去加油，经过观察他发现了一个有趣的现象：爸爸和妈妈的加油习惯是不同的.爸爸每次加油都说：“师傅，给我加250元的油”，而妈妈则说“师傅帮我把油箱加满”.这位同学若有所思，如果爸爸､妈妈都加油两次，两次的加油价格不同，妈妈每次加满油箱；爸爸每次加250元的油，我们规定谁的平均单价低谁就合算，那么请问爸爸､妈妈谁更合算呢？（）

A、妈妈 B、爸爸 C、一样 D、不确定

查看试题解析
4. 设 $a$ 为实数，定义在 $R$ 上的偶函数 $f (x)$ 满足： $f (x)$ 在 $[0 ， + \infty)$ 上的表达式为 $f (x) = 3 x^{2} + 2 x - 4$ ，则使得 $f (2 a) > f (a + 1)$ 成立的 $a$ 的取值范围为（）

A、 $(- \infty ， - \frac{1}{3}) ∪ (1 ， + \infty)$ B、 $(- \frac{1}{3} ， 1)$ C、 $(- 1 ， \frac{1}{3})$ D、 $(- \infty ， 1)$

查看试题解析
5. 某同学在课外阅读时了解到概率统计中的切比雪夫不等式，该不等式可以使人们在随机变量 $X$ 的期望 $E (X)$ 和方差 $D (X)$ 存在但其分布末知的情况下，对事件“ $| X - E (X) | ⩾ ε$ ”的概率作出上限估计，其中 $ε$ 为任意正实数.切比雪夫不等式的形式为： $P (| X - E (X) | ⩾ ε) ⩽ f (D (X) ， ε)$ ，其中 $f (D (X) ， ε)$ 是关于 $D (X)$ 和 $ε$ 的表达式.由于记忆模糊，该同学只能确定 $f (D (X) ， ε)$ 的具体形式是下列四个选项中的某一种.请你根据所学相关知识，确定该形式是（）

A、 $D (X) \cdot ε^{2}$ B、 $\frac{1}{D (X) \cdot ε^{2}}$ C、 $\frac{ε^{2}}{D (X)}$ D、 $\frac{D (X)}{ε^{2}}$

查看试题解析
6. 在复平面内，复数z满足 $(1 + i) z = a + 1 + b i (a ， b \in R)$ ，且z所对应的点在第一象限或坐标轴的非负半轴上，则a+2b的最小值为（）

A、-2 B、-1 C、1 D、2

查看试题解析
7. 铁路总公司关于乘车行李规定如下：乘坐动车组列车携带品的外部尺寸长、宽、高之和不超过 $130 c m$ ．设携带品外部尺寸长、宽、高分别为 $a ， b ， c$ （单位： $c m$ ），这个规定用数学关系式表示为（）．

A、 $a + b + c < 130$ B、 $a + b + c > 130$ C、 $a + b + c \leq 130$ D、 $a + b + c \geq 130$

查看试题解析
8. 甲乙两车主约定好同时到同一加油站为自己的小车加同一标号的汽油，受国际油价影响，汽油的价格是变化的（不是常数），而他们的加油方式又不一样，甲车主每次总是加200元的油，乙车主每次加30升汽油，则甲乙两种加油方式相比更合算的是（）

A、甲 B、乙 C、一样 D、不能确定

查看试题解析
9. 某公司准备对一项目进行投资，提出两个投资方案：方案 $A$ 为一次性投资300万；方案 $B$ 为第一年投资80万，以后每年投资20万.下列不等式表示“经过 $n$ 年之后，方案 $B$ 的投入不少于方案 $A$ 的投入”的是（）

A、 $80 + 20 n \geq 300$ B、 $80 + 20 n \leq 300$ C、 $80 + 20 (n - 1) \leq 300$ D、 $80 + 20 (n - 1) \geq 300$

查看试题解析
10. 某商品A以每件2元的价格出售时，销售量为10万件.经过调查，单价每提高0.2元，销售量减少5000件，要使商品A销售总收入不少于22.4万元，该商品A的单价可定为（）

A、2.6元 B、2.8元 C、3元 D、3.2元

查看试题解析

二、填空题

11. 若不等式 $e^{x} \geq (a + 1) x + b$ 对一切 $x \in R$ 恒成立，则 $(a + 1) b$ 的最大值为．

查看试题解析
12. 在 $△ A B C$ 中， $t a n B = 4 t a n A$ ，则当 $B - A$ 取最大值时， $s i n C =$ .

查看试题解析
13. 某阅读平台为了吸引用户，决定对部分图书开展限时免费阅读活动．当提供免费阅读的图书为a本时，其用户人数 $f (a) = 80 [\frac{a}{3}] + 32$ （ $[a]$ 表示不大于a的最大整数）．当 $a = 100$ 时，用户人数为；若该平台想通过本次活动使用户人数不少于5000，则至少需要提供免费阅读的图书数量为．

查看试题解析
14. 新学期开学之际，某学生计划用不超过15元的资金购买单价分别为1元的笔记本和2元的圆珠笔.已知该学生至少要购买8本笔记本，且至少要购买2支圆珠笔，则不同的选购方式有种，（用数字作答）

查看试题解析
15. 一种药在病人血液中的量保持在2000mg以上时才有疗效，而低于1280mg时病人就有危险.现给某病人静脉注射了这种药2500mg，如果药在血液中以每小时20%的比例衰减，那么最迟必须在注射后小时前向病人的血液补充这种药.

查看试题解析
16. 2020年是全国决胜脱贫攻坚之年，“一帮一扶”工作组进驻某山区帮助农民脱贫，发现该山区盛产苹果、梨子、猕猴桃，工作人员文明在线上进行直播带货活动，促销方案如下：若一次购买水果总价不低于200元，则顾客少付款m元，每次订单付款成功后，农民会收到支付款的80%，在促销活动中，为了使得农民收入不低于总价的70%，则m的最大值为.

查看试题解析
17. 某学生社会实践小组调查发现，某商品的供应量与商品的销售价格有如下关系：当商品供应的增加量不超过原供应量时，商品的销售价格的降低量与商品供应的增加量的算术平方根成正比.假设商品的原供应量为1个单位，当商品供应量增加一倍时，销售价格降为原来的一半.若商品的销售价格不高于原来的80% ，则供应量至少增加为原来的倍.

查看试题解析
18. 若对任意 $x \in [1, 2]$ 且 $y \in [2, 3]$ ，不等式 $x y ⩽ a x^{2} + 2 y^{2}$ 恒成立，则实数a的取值范围是.

查看试题解析
19. 为满足人民群众便利消费、安全消费、放心消费的需求，某社区农贸市场管理部门规划建造总面积为 $2400 m^{2}$ 的新型生鲜销售市场．市场内设蔬菜水果类和肉食水产类店面共80间．每间蔬菜水果类店面的建造面积为 $28 m^{2}$ ，月租费为 $x$ 万元；每间肉食水产店面的建造面积为 $20 m^{2}$ ，月租费为0.8万元．全部店面的建造面积不低于总面积的80%，又不能超过总面积的85%．①两类店面间数的建造方案为种．②市场建成后所有店面全部租出，为保证任何一种建设方案平均每间店面月租费不低于每间蔬菜水果类店面月租费的90%，则 $x$ 的最大值为万元．

查看试题解析
20. 张军自主创业，在网上经营一家干果店，销售的干果中有松子、开心果、腰果、核桃，价格依次为120元/千克、80元/千克、70元/千克、40元千克，为增加销量，张军对这四种干果进行促销:一次购买干果的总价达到150元，顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后，张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克，需要支付180元，则x=；

②在促销活动中，为保证张军每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为.

查看试题解析

三、解答题

21. 随着我国经济发展、医疗消费需求增长、人们健康观念转变以及人口老龄化进程加快等影响，医疗器械市场近年来一直保持了持续增长的趋势．某医疗器械公司为了进一步增加市场力，计划改进技术生产某产品．已知生产该产品的年固定成本为300万元，最大产能为100台，每生产 $x$ 台，需另投入成本 $G (x)$ 万元，且 $G (x) = {\begin{array}{l} 2 x^{2} + 80 x ， 0 < x \leq 40 \\ 201 x + \frac{3600}{x} - 2100 ， 40 < x \leq 100 \end{array}$ ，由市场调研知，该产品每台的售价为200万元，且全年内生产的该产品当年能全部销售完．

(1)、写出年利润 $W (x)$ 万元关于年产量 $x$ 台的函数解析式（利润=销售收入-成本）；

(2)、当该产品的年产量为多少时，公司所获利润最大？最大利润是多少？

查看试题解析
22. 某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为200吨，最多为500吨，月处理成本y（元）与月处理量x（吨）之间的函数关系可近似地表示为 $y = \frac{1}{2} x^{2} - 200 x + 80000$ ，且每处理一吨二氧化碳得到可利用的化工产品价值为100元.则

(1)、该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低，最低是多少？

(2)、每月需要国家至少补贴多少元才能使该单位不亏损

查看试题解析
23. 浙江正聚焦“富民、强村”以农村产业振兴为基础，实现乡村振兴乃至共同富裕．某乡镇以“共富果园”为目标，促进农业产业高质量发展，经调研发现，某特色果树的单接产量 $W$ （单位：千克）与施用肥料 $x$ （单位：千克）满足如下关系： $W (x) = {\begin{array}{l} 5 (x^{2} + 5) ， 0 \leq x \leq 2 \\ 60 - \frac{60}{x + 3} ， 2 < x \leq 6 \end{array}$ ，另肥料成本投入为 $10 x$ 元，其它成本投入（如培育管理、施肥等人工费）为 $20 x$ 元．已知这种水果的市场售价大约为18元/千克，且销路畅通供不应求，记该水果树的单株利润为 $f (x)$ （单位：元）．

(1)、写出 $f (x)$ 关于 $x$ 的函数解析式；

(2)、当施用肥料为多少千克时，该果树的单株利润最大？最大利润是多少？

查看试题解析
24. 丽水市某工厂生产甲产品的年固定成本为200万元，若甲产品的年产量为 $x$ 万件，则需另投入成本 $t (x) ($ 万元）．已知甲产品年产量不超过100万件时， $t (x) = \frac{1}{4} x^{2} + 14 x$ ；甲产品年产量大于100万件时， $t (x) = 51 x + \frac{10000}{x - 60} - 1450$ ．因设备限制，甲产品年产量不超过200万件．现已知甲产品的售价为50元/件，且年内生产的甲产品能全部销售完．设该厂生产甲产品的年利润为 $L$ （万元）．

(1)、写出 $L$ 关于 $x$ 的函数解析式 $L (x)$ ；

(2)、当年产量 $x$ 为多少时，该厂生产甲产品所获的利润 $L$ 最大？

查看试题解析
25. 中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措，作为中欧铁路在东北地区的始发站，沈阳某火车站正在不断建设，目前车站准备在某仓库外，利用其一侧原有墙体，建造一面高为3米，底面积为12平方米，且背面靠墙的长方体形状的保管员室，由于保管员室的后背靠墙，无需建造费用，因此，甲工程队给出的报价如下屋子前面新建墙体的报价为每平方米400元，左右两面新建墙体的报价为每平方米150元，屋顶和地面以及其他报价共计7200元，设屋子的左右两面墙的长度均为x米 $2 \leq x \leq 6$ .

(1)、当左右两面墙的长度为多少米时，甲工程队的报价最低？

(2)、现有乙工程队也参与此保管员室建造竞标，其给出的整体报价为 $\frac{900 a (1 + x)}{x}$ 元（a>0）；若无论左右两面墙的长度为多少米，乙工程队都能竞标成功（报价低的工程队中标），求a的取值范围.

查看试题解析
26. 已知 $a$ ， $b$ 为正数，函数 $f (x) = | x - a | + | x + b |$ 的值域为 $[1 - c ， + \infty)$ .

(1)、若 $c = - 1$ ，证明： $a + b \geq 2 a b$ ；

(2)、若 $c > 0$ ，证明： $\frac{(1 - a) (1 - b) (1 - c)}{a b c} \geq 8$ .

查看试题解析
27. 2020年11月23日，贵州宣布最后9个深度贫困县退出贫困县序列，这不仅标志着贵州省66个贫困县实现整体脱贫，这也标志着国务院扶贫办确定的全国832个贫困县全部脱贫摘帽，全国脱贫攻坚目标任务已经完成.在脱贫攻坚过程中，某地县乡村三级干部在帮扶走访中得知某贫困户的实际情况后，为他家量身定制了脱贫计划，政府无息贷款10万元给该农户种养羊，每万元可创造利润0.15万元.若进行技术指导，养羊的投资减少了 $x$ $(x > 0)$ 万元，且每万元创造的利润变为原来的 $(1 + 0.25 x)$ 倍.现将养羊少投资的 $x$ 万元全部投资网店，进行农产品销售，则每万元创造的利润为 $0.15 (a - 0.875 x)$ 万元，其中 $a > 0$ .

(1)、若进行技术指导后养羊的利润不低于原来养羊的利润，求 $x$ 的取值范围；

(2)、若网店销售的利润始终不高于技术指导后养羊的利润，求 $a$ 的最大值.

查看试题解析
28. 国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准，新标准规定，车辆驾驶人血液中的酒精含量大于或等于20毫克/百毫升、小于80毫克/百毫升的行为饮酒驾车，血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车，经过反复试验，喝一瓶啤酒后酒精在人体血液内的变化规律“散点图”如下：

该函数模型如下，

$f (x) = {\begin{array}{l} 44.21 sin (\frac{π}{3} x) + 0.21 ， 0 \leq x < 2 \\ 54.27 e^{- 0.3 x} + 10.18 ， x \geq 2 \end{array}$ .

根据上述条件，回答以下问题：

(1)、试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值？最大值是多少？

(2)、试计算喝1瓶啤酒后多少小时才可以驾车？（时间以整小时计）（参考数据： $ln 9.82 \approx 2.28 ， ln 10.18 \approx 2.32 ， ln 54.27 \approx 3.99$ ）

查看试题解析
29. 此前，美国政府颁布了针对中国企业华为的禁令，禁止各国及各国企业向华为出售含有美国技术或软件设计的产品，否则出售者本身也会受到制裁.这一禁令在9月15日正式生效，迫于这一禁令的压力，很多家企业被迫停止向华为供货，对华为电子设备的发展产生不良影响.为适应发展的需要，某企业计划加大对芯片研发部的投入，据了解，该企业研发部原有100名技术人员，年人均投入a万元，现把原有技术人员分成两部分：技术人员和研发人员，其中技术人员x名（ $x \in N$ 且 $45 \leq x \leq 75$ ），调整后研发人员的年人均投入增加4x%，技术人员的年人均投入调整为 $a (m - \frac{2 x}{25})$ 万元.

(1)、要使这 $100 - x$ 名研发人员的年总投入不低于调整前100名技术人员的年总投入，求调整后的技术人员的人数最多多少人?

(2)、是否存在这样的实数m，使得技术人员在已知范围内调整后，同时满足以下两个条件：①技术人员的年均投入始终不减少；②研发人员的年总投入始终不低于技术人员的年总投入，存在，求出m的范围；若不存在，说明理由.

查看试题解析
30. 汤姆今年年初用16万元购进一辆汽车，每天下午跑滴滴出租车，经估算，每年可有16万元的总收入，已知使用x年( $x \in N^{*}$ )所需的各种费用（维修、保险、耗油等）总计为 $(x^{2} + 2 x)$ 万元（今年为第一年）．

(1)、该出租车第几年开始赢利（总收入超过总支出）？

(2)、该车若干年后有两种处理方案：
①当赢利总额达到最大值时，以1万元价格卖出；

②当年平均赢利达到最大值时，以10万元卖出.

试问哪一种方案较为合算？请说明理由．

查看试题解析