【备考2024】高考数学（代数版块）细点逐一突破复习专练：基本不等式1

试卷更新日期：2023-08-16 类型：二轮复习

进入出卷网下载

一、选择题

1. 函数 $f (x)$ 的图象如下图所示，则 $f (x)$ 的解析式可能为（）

A、 $\frac{5 (e^{x} - e^{- x})}{x^{2} + 2}$ B、 $\frac{5 s i n x}{x^{2} + 1}$ C、 $\frac{5 (e^{x} + e^{- x})}{x^{2} + 2}$ D、 $\frac{5 c o s x}{x^{2} + 1}$

查看试题解析
2. 对任意x，y， $x^{2} + y^{2} - x y = 1$ ，则（）

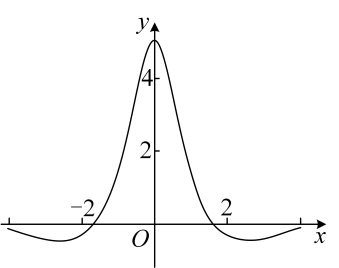A、 $x + y \leq 1$ B、 $x + y \geq - 2$ C、 $x^{2} + y^{2} \leq 2$ D、 $x^{2} + y^{2} \geq 1$

查看试题解析
3. 下列函数中最小值为4的是（）

A、 $y = x^{2} + 2 x + 4$ B、 $y = | \sin x | + \frac{4}{| \sin x |}$ C、 $y = 2^{x} + 2^{2 - x}$ D、 $y = \ln x + \frac{4}{\ln x}$

查看试题解析
4. 已知 $F_{1}$ 、 $F_{2}$ 为椭圆与双曲线的公共焦点，P是其一个公共点， $∠ F_{1} P F_{2} = 60 °$ ，则椭圆与双曲线离心率之积的最小值为（）

A、 $2 \sqrt{3}$ B、1 C、 $\frac{\sqrt{3}}{2}$ D、2

查看试题解析
5. 当 $x$ ， $y \in (0 ， + \infty)$ 时， $\frac{4 x^{4} + 17 x^{2} y + 4 y^{2}}{x^{4} + 2 x^{2} y + y^{2}} < \frac{m}{4}$ 恒成立，则m的取值范围是（）

A、 $(25 ， + \infty)$ B、 $(26 ， + \infty)$ C、 $(\frac{99}{4} ， + \infty)$ D、 $(27 ， + \infty)$

查看试题解析
6. 点 $A (x_{0} ， y_{0}) (x_{0} > 1 ， y_{0} < 0) ， B ， C$ 均在抛物线 $y^{2} = 4 x$ 上，若直线 $A B ， A C$ 分别经过两定点 $(- 1 ， 0) ， M (1 ， 4)$ ，则 $B C$ 经过定点 $N$ ，直线 $B C ， M N$ 分别交 $x$ 轴于 $D ， E$ ， $O$ 为原点，记 $| O D | = a ， | D E | = b$ ，则 $\frac{a^{2}}{a + 1} + \frac{b^{2}}{b + 3}$ 的最小值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{5}$

查看试题解析
7. 已知定义在 $R$ 上的偶函数 $f (x) = | x - m + 1 | - 2$ ，若正实数a、b满足 $f (a) + f (2 b) = m$ ，则 $\frac{1}{a} + \frac{2}{b}$ 的最小值为（）

A、 $\frac{9}{5}$ B、9 C、 $\frac{8}{5}$ D、8

查看试题解析
8. 在空间直角坐标系 $O - x y z$ 中，已知定点 $A (2 ， 1 ， 0)$ ， $B (0 ， 2 ， 0)$ 和动点 $C (0 ， t ， t + 2) (t \geq 0)$ .若 $△ O A C$ 的面积为 $S$ ，以 $O ， A ， B ， C$ 为顶点的锥体的体积为 $V$ ，则 $\frac{V}{S}$ 的最大值为（）

A、 $\frac{2}{15} \sqrt{5}$ B、 $\frac{1}{5} \sqrt{5}$ C、 $\frac{4}{15} \sqrt{5}$ D、 $\frac{4}{5} \sqrt{5}$

查看试题解析
9. 已知 $F_{1} 、 F_{2}$ 分别是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的左、右焦点， $P$ 为双曲线右支上的任意一点且 $\frac{| P F_{1} |^{2}}{| P F_{2} |} = 8 a$ ，则双曲线离心率的取值范围是（）

A、(1，2] B、[2 + $\infty$ ) C、(1，3] D、[3，+ $\infty$ )

查看试题解析
10. 若a，b，c均为正数，且满足 $a^{2} + 3 a b + 3 a c + 9 b c = 18$ ，则 $2 a + 3 b + 3 c$ 的最小值是（）

A、6 B、 $4 \sqrt{6}$ C、 $6 \sqrt{2}$ D、 $6 \sqrt{3}$

查看试题解析
11. 下列判断正确的是（）

A、若 $x > 1$ ，则 $x + \frac{4}{x - 1}$ 的最小值是5 B、若 $x < y$ ，则 $\frac{1}{x} > \frac{1}{y}$ C、若 $x \in (0 ， π)$ ，则 $s i n x + \frac{2}{s i n x}$ 的最小值是 $2 \sqrt{2}$ D、若 $x > y$ ，则 $x^{2} > y^{2}$

查看试题解析
12. 已知 $a > 1$ ， $b > 1$ ，且 $l o g_{2} \sqrt{a} = l o g_{b} 4$ ，则ab的最小值为（）

A、4 B、8 C、16 D、32

查看试题解析
13. 已知a，b都是正实数，则下列不等式中恒成立的是（）

A、 $(a + 4 b) (\frac{1}{a} + \frac{1}{b}) \geq 9$ B、 $(a + b) (\frac{1}{a} + \frac{1}{b}) \geq 6$ C、 $a^{2} + \frac{5}{2} > 3 a$ D、 $\frac{a}{a^{2} - a + 1} \leq \frac{1}{2}$

查看试题解析

二、填空题

14. 在 $△ A B C$ 中， $∠ A = 6 0^{∘}$ ， $B C = 1$ ，点 $D$ 为 $A B$ 的中点，点 $E$ 为 $C D$ 的中点，若设 $\vec{A B} = \vec{a} ， \vec{A C} = \vec{b}$ ，则 $\vec{A E}$ 可用 $\vec{a} ， \vec{b}$ 表示为；若 $\vec{B F} = \frac{1}{3} \vec{B C}$ ，则 $\vec{A E} \cdot \vec{A F}$ 的最大值为．

查看试题解析
15. $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，若 $a c o s B + 2 b c o s A = 0$ ，则 $\frac{t a n A}{t a n B} =$ ， $t a n C$ 的最大值是．

查看试题解析
16. $P$ 是抛物线 $x^{2} = 4 y$ 准线为 $l$ 上一点， $A ， B$ 在抛物线上， $P A ， P B$ 的中点也在抛物线上，直线 $A B$ 与 $l$ 交于点 $Q$ ，则 $| P Q |$ 的最小值为.

查看试题解析
17. 已知正数x，y满足 $x (x + 2 y) = 9$ ，则 $\frac{y}{{(x + y)}^{2}}$ 的最大值为．

查看试题解析
18. 在 $△ A B C$ 中， $∠ A B C = \frac{π}{3}$ ，点 $D$ 在线段 $A C$ 上，且 $A D = 3 D C$ ， $B D = 4$ ，则 $△ A B C$ 面积的最大值为．

查看试题解析
19. 若直线 $\frac{x}{a} + \frac{y}{b} = 1 (a > 0 ， b > 0)$ 过点 $(2 ， 3)$ ，则 $2 a + b$ 的最小值为．

查看试题解析
20. 足球是一项很受欢迎的体育运动.如图，某标准足球场的 $B$ 底线宽 $A B = 72$ 码，球门宽 $E F = 8$ 码，球门位于底线的正中位置.在比赛过程中，攻方球员带球运动时，往往需要找到一点 $P$ ，使得 $∠ E P F$ 最大，这时候点 $P$ 就是最佳射门位置.当攻方球员甲位于边线上的点 $O$ 处（ $O A = A B$ ， $O A ⊥ A B$ ）时，根据场上形势判断，有 $\vec{O A}$ 、 $\vec{O B}$ 两条进攻线路可供选择.若选择线路 $\vec{O A}$ ，则甲带球码时， $A P O$ 到达最佳射门位置；若选择线路 $\vec{O B}$ ，则甲带球码时，到达最佳射门位置.

查看试题解析
21. 已知 $F_{1}$ 、 $F_{2}$ 分别为椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左、右焦点， $P$ 是过椭圆右顶点且与长轴垂直的直线上的动点，则 $s i n ∠ F_{1} P F_{2}$ 的最大值为．

查看试题解析
22. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左､右焦点分别为 $F_{1} ， F_{2}$ ，离心率为 $e$ ，点 $P$ 在椭圆上，连接 $P F_{1}$ 并延长交 $C$ 于点 $Q$ ，连接 $Q F_{2}$ ，若存在点 $P$ 使 $| P Q | = | Q F_{2} |$ 成立，则 $e^{2}$ 的取值范围为.

查看试题解析
23. 已知两个正数 $a$ ， $b$ 的几何平均值为1，则 $a^{2} + b^{2}$ 的最小值为．

查看试题解析
24. 若不等式 $a x^{2} - 6 x + 3 > 0$ 对 $x \in R$ 恒成立，则a的取值范围是， $a + \frac{9}{a - 1}$ 的最小值为．

查看试题解析

三、解答题

25. 已知a，b，c都是正数，且 $a^{\frac{3}{2}} + b^{\frac{3}{2}} + c^{\frac{3}{2}} = 1$ ，证明：

(1)、 $a b c \leq \frac{1}{9}$ ；

(2)、 $\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b} \leq \frac{1}{2 \sqrt{a b c}}$ ．

查看试题解析
26. 在锐角 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $s i n (2 A + B) = 2 s i n A (1 - c o s C)$ .

(1)、证明： $b = 2 a$ ；

(2)、求 $\frac{3 s i n^{2} A + s i n^{2} B}{2 s i n A s i n C} + c o s B$ 的取值范围.

查看试题解析
27. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分别 $a ， b ， c$ ，且 $b c o s A + a c o s B = 2 c c o s A$

(1)、求角A的值；

(2)、已知 $D$ 在边 $B C$ 上，且 $B D = 3 D C ， A D = 3$ ，求 $△ A B C$ 的面积的最大值

查看试题解析
28. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对边分别记为 $a$ ， $b$ ， $c$ .条件①： $\frac{s i n A}{1 - c o s A} = \frac{s i n 2 B}{1 + c o s 2 B}$ ；条件②： $s i n C s i n (B - A) = s i n B s i n (C - A)$ .从条件①、条件②这两个条件中选择一个作为已知.

(1)、证明： $B = C$ ；

(2)、求 $\frac{2 a + b}{c} + \frac{1}{c o s B}$ 的最小值.

查看试题解析
29. 已知函数 $f (x) = 2 \sqrt{x^{2} + 2 a x + a^{2}} - 2 | x - b | (a > 0 ， b > 0)$ 的最大值为2．

(1)、求 $a + b$ 的值；

(2)、证明： $\frac{1}{a} + \frac{4}{b} + \frac{4}{(3 a + 1) b} \geq 12$ ．

查看试题解析
30. 已知 $a > 0$ ， $b > 0$ ，且 $a + b = 2$ ．

(1)、求 $a^{2} + b^{2}$ 的最小值；

(2)、证明： $\sqrt{a + 1} + \sqrt{b + 1} \leq 2 \sqrt{2}$ ．

查看试题解析
31. 已知函数 $f (x) = | x - t | + | x + t |$ ， $t \in R$ ．

(1)、若 $t = 1$ ，求不等式 $f (x) \leq 8 - x^{2}$ 的解集；

(2)、已知 $m + n = 4$ ，若对任意 $x ∈ R$ ，都存在 $m > 0$ ， $n > 0$ 使得 $f (x) = \frac{4 m^{2} + n}{m n}$ ，求实数 $t$ 的取值范围．

查看试题解析
32. 已知函数 $f (x) = | x - 1 | + | x - 3 |$ .

(1)、解不等式 $f (x) \leq x + 1$ ；

(2)、设函数 $f (x)$ 的最小值为c，正实数a，b满足 $a + b = c$ ，求 $\frac{1}{a} + \frac{1}{b + 1}$ 的最小值.

查看试题解析
33. 已知 $a > 0$ ， $b > 0$ ， $a^{\frac{3}{2}} + b^{\frac{3}{2}} = 2$ ，证明：

(1)、 $(a^{\frac{1}{2}} + b^{\frac{1}{2}}) (a^{\frac{5}{2}} + b^{\frac{5}{2}}) \geq 4$ ；

(2)、 $a^{\frac{1}{2}} + b^{\frac{1}{2}} \leq 2$ ．

查看试题解析
34. 已知函数 $f (x) = e^{m x - 1} - x$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、当 $m > 0$ 时，函数 $g (x) = f (x) - \frac{l n x + 1}{m} + x$ 恰有两个零点.
（i）求m的取值范围；
（ii）证明： $g (x) > m^{\frac{1}{m}} - m^{- \frac{1}{m}}$ .

查看试题解析
35. 已知函数 $f (x) = | x - 2 | + | x + 2 |$ .

(1)、求不等式 $f (x) \geq 2 x + 4$ 的解集；

(2)、若 $f (x)$ 的最小值为 $k$ ，且实数 $a ， b ， c$ ，满足 $a (b + c) = k$ ，求证： $2 a^{2} + b^{2} + c^{2} \geq 8$ .

查看试题解析