【备考2024】高考数学(代数版块)细点逐一突破复习专练:一元二次不等式的解法
试卷更新日期:2023-08-16 类型:二轮复习
一、选择题
-
1. 设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=( )A、–4 B、–2 C、2 D、42. 不等式 的解集是()A、 B、 C、 D、3. 已知集合 , 则( )A、 B、 C、 D、4. 在区间上随机地抽取一个实数x,则x满足的概率为( )A、 B、 C、 D、5. 已知集合 , , 则( )A、 B、 C、 D、6. 已知不等式的解集为 , 则不等式的解集为( )A、 B、 C、 D、7. 已知集合 , , 则( )A、 B、 C、 D、8. 已知集合M={x|0≤x<2},N={x|x2-2x-3<0},则M∩N=( )A、{x|0≤x<1} B、{x|0≤x<2} C、{x|0≤x≤1} D、{x|0≤x≤2}9. 以下四个命题中,真命题的是( )A、不等式的解集为 B、若 , 则 C、若 , 则 D、若 , , 则10. 设 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件11. 的一个充分不必要条件是( )A、 B、 C、 D、或12. 下列四个不等式中,解集为是( )A、 B、 C、 D、
二、填空题
-
13. 已知函数 的部分图像如图所示,则满足条件 的最小正整数x为。
 14. 设 ,使不等式 成立的 的取值范围为.15. 若不等式恒成立,则a的取值范围是.16. 已知函数的图像如图所示,则不等式的解集是.
14. 设 ,使不等式 成立的 的取值范围为.15. 若不等式恒成立,则a的取值范围是.16. 已知函数的图像如图所示,则不等式的解集是.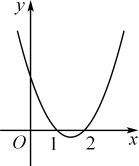 17. 已知函数(且),若关于的不等式的解集为 , 其中 , 则实数的取值范围是 .18. 若实数满足不等式 , 则的取值范围是.19. 已知函数 , 若 , 则实数的取值范围是 .20. 设是曲线上的动点,且.则的取值范围是.21. 设函数 , 若关于的不等式的解集为空集,则实数的取值范围为.22. 已知关于的一元二次不等式的解集为 , 则关于的不等式的解集为 .23. 已知集合 , 函数满足不等式的解集为P,则函数 . (写出一个符合条件的即可)24. 不等式的解集为 .
17. 已知函数(且),若关于的不等式的解集为 , 其中 , 则实数的取值范围是 .18. 若实数满足不等式 , 则的取值范围是.19. 已知函数 , 若 , 则实数的取值范围是 .20. 设是曲线上的动点,且.则的取值范围是.21. 设函数 , 若关于的不等式的解集为空集,则实数的取值范围为.22. 已知关于的一元二次不等式的解集为 , 则关于的不等式的解集为 .23. 已知集合 , 函数满足不等式的解集为P,则函数 . (写出一个符合条件的即可)24. 不等式的解集为 .三、解答题
-
25. 已知函数f(x)=lnx+ax2+(2a+1)x.(1)、讨论f(x)的单调性;(2)、当a<0时,证明f(x)≤﹣ ﹣2.26. 设 , .(1)、当时,求满足的的取值范围;(2)、求证:函数在区间上是严格增函数.27. 已知函数.(1)、当时,解关于x的不等式;(2)、若不等式的解集为D,且 , 求m的取值范围.28. 已知 , , 全集 .(1)、若 , 求;(2)、若 , 求实数的取值范围.29. 设是公差不为0的等差数列的前项和,若 , .(1)、求数列的通项公式;(2)、求使的的最大值.30. 已知函数的最小值为 , 方程有两个实根和6.(1)、求函数的解析式;(2)、求关于的不等式的解集.31. 设函数.(1)、若关于的不等式有实数解,求实数的取值范围;(2)、若不等式对于实数时恒成立,求实数的取值范围;(3)、解关于的不等式:.32. 已知函数.(1)、若 , 解不等式;(2)、解关于的不等式.