【备考2024】高考数学(代数版块)细点逐一突破复习专练:不等关系与不等式
试卷更新日期:2023-08-16 类型:二轮复习
一、选择题
-
1. 若a>b>0,c<d<0,则一定有( )A、> B、< C、> D、<2. 设a=log36,b=log510,c=log714,则( )A、c>b>a B、b>c>a C、a>c>b D、a>b>c3. 如果a<b<0,那么下列不等式成立的是( )A、 B、ab<b2 C、﹣ab<﹣a2 D、4. 已知a,b>0且a≠1,b≠1,若logab>1,则( )A、(a﹣1)(b﹣1)<0 B、(a﹣1)(a﹣b)>0 C、(b﹣1)(b﹣a)<0 D、(b﹣1)(b﹣a)>05. 已知x,y∈R,且x>y>0,则( )
A、﹣ >0 B、sinx﹣siny>0 C、( )x﹣( )y<0 D、lnx+lny>06. 下列结论错误的是( )A、若 , 则 B、若 , 则 C、若 , , 则 D、若 , 的最小值为7. 如果 , 那么下列式子中一定成立的是( )A、 B、 C、 D、8. 下列说法正确的是( )A、若 , 则的范围为 B、若在第一象限,则在第一、二象限 C、要得到函数的图像,只需将函数向右平移个单位 D、在中,若 , 则的形状一定是钝角三角形9. 十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“”作为符号使用,后来英国数学家哈利奥特首次使用“”和“”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.若 , , , 则下列命题正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则 D、若 , 则10. 已知函数 , 若 , 则实数的取值范围( )A、 B、 C、 D、11. 已知 , 则( )A、 B、 C、 D、二、填空题
-
12. , 若 , 且为的两实根.则的取值范围为 .13. 已知 , , 则ab的最小值为 , 最大值为 .14. 设a为实数,若关于x的一元一次不等式组的解集中有且仅有4个整数,则a的取值范围是.15. 已知 是 的充分不必要条件,则实数 的取值范围是.16. 限速40km∕h 的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km∕h,写成不等式就是 .17. 已知 幂函数 在 上单调递减,则 是 的条件.(选填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)18. 已知函数 ,则不等式 的解集为 .19. 在一次调查中,甲、乙、丙、丁四位同学阅读量有如下关系:同学甲、丙阅读量之和与乙、丁阅读量之和相同,同学甲、乙阅读量之和大于丙、丁阅读量之和,丁的阅读量大于乙、丙阅读量之和.那么这四名同学按阅读量从大到小的排序依次为.20. 已知 ,类比于我们学习过的“糖水加糖甜更甜”的原理,提炼出“向一杯糖水中加入水,则糖水变淡了”的不等关系式为
三、解答题
-
21. 已知函数f(x)=ex , x∈R.(1)、若直线y=kx+1与f (x)的反函数g(x)=lnx的图象相切,求实数k的值;(2)、设x>0,讨论曲线y=f (x) 与曲线y=mx2(m>0)公共点的个数.(3)、设a<b,比较 与 的大小,并说明理由.22. 若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0,满足 .(1)、求f(1)的值;(2)、若f(6)=1,解不等式f(x+3)-f()<2.23. 已知函数 , 从下面两个条件中选择一个求出 , 并解不等式 . ①函数是偶函数;②函数是奇函数.24. 已知1≤a+b≤4,-1≤a-b≤2,求4a-2b的取值范围.25.(1)、设 , , 证明:;(2)、设 , , , 证明:.26. 已知曲线 和曲线 交于A,B两点(点A在第二象限).过点A作斜率为 的直线 交曲线M于点C(不同于点A),过点 作斜率为 的直线 交曲线 于E,F两点,且 .
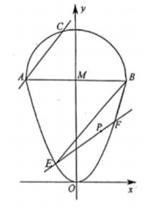
(Ⅰ)求 的取值范围;
(Ⅱ)设 的面积为S,求 的最大值.