重庆市南岸区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 把多项式a2+2a分解因式得( )A、a(a+2) B、a(a-2) C、(a+2)2 D、(a+2)(a-2)2. 下面四个交通标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知 , 下列一定成立的是( )A、 B、 C、 D、4. 分式 有意义的条件是( )A、x=-3 B、x≠-3 C、x≠3 D、x≠05. 在中(如图),连接 , 已知 , , 则( )
3. 已知 , 下列一定成立的是( )A、 B、 C、 D、4. 分式 有意义的条件是( )A、x=-3 B、x≠-3 C、x≠3 D、x≠05. 在中(如图),连接 , 已知 , , 则( )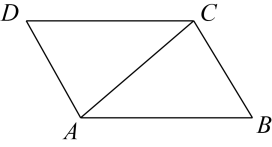 A、 B、 C、 D、6. 方程的解是( )A、 B、 C、 D、7. 已知一个多边形的内角和等于900º,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 如图,在中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线交边于点E.若 , , , 则的长为( )
A、 B、 C、 D、6. 方程的解是( )A、 B、 C、 D、7. 已知一个多边形的内角和等于900º,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 如图,在中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线交边于点E.若 , , , 则的长为( ) A、 B、6 C、 D、79. 如图,在中, , , 点D是边上一点,连接 , 把绕点D旋转至 , 连接 . 若 , ∠DEB=90°,则的长为( )
A、 B、6 C、 D、79. 如图,在中, , , 点D是边上一点,连接 , 把绕点D旋转至 , 连接 . 若 , ∠DEB=90°,则的长为( ) A、1 B、 C、 D、210. 关于x的一元一次不等式组的解集是 , 且关于y的分式方程有非负整数解,则符合条件的所有整数a的和是( )A、0 B、1 C、5 D、6
A、1 B、 C、 D、210. 关于x的一元一次不等式组的解集是 , 且关于y的分式方程有非负整数解,则符合条件的所有整数a的和是( )A、0 B、1 C、5 D、6二、填空题
-
11. 不等式的解集是 .12. 如图,如果只用一种若干个正多边形镶嵌整个平面,如图是由其拼成的无缝隙且不重叠的图形的一部分,这种正多边形的边数是 .
 13. 在中, , , 则的度数为 .14. 若 , 则 .15. 如图,已知 , , 当时,x的取值范围为 .
13. 在中, , , 则的度数为 .14. 若 , 则 .15. 如图,已知 , , 当时,x的取值范围为 . 16. 如图,在中,平分若则 .
16. 如图,在中,平分若则 .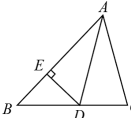 17. 如图, , , D为上一点, , , 交于点E,点F为直线上一点,则的最小值为 .
17. 如图, , , D为上一点, , , 交于点E,点F为直线上一点,则的最小值为 . 18. 用表示十位数字为m,个位数字为5的两位数,其中 , 且m是整数,例如,当时,表示的两位数是65
18. 用表示十位数字为m,个位数字为5的两位数,其中 , 且m是整数,例如,当时,表示的两位数是65当时,;
当时,;
……
(1)、请仿照上面的等式,用含m的式子表示:;(2)、若与的差为6425,则 .三、解答题
-
19. 如图所示,在平面直角坐标系内,三个顶点坐标分别为 , , .
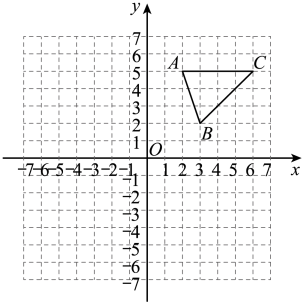
⑴在图中,画出向左平移8个单位得到的;
⑵在图中,画出以点O为对称中心,与成中心对称图形的;
⑶直接写出点 , , 的坐标.
20. 解不等式组 ,并把它的解集在数轴上表示出来. 21. 计算:(1)、;(2)、22. 在学习三角形的过程中,亮亮遇到这样一个问题:如图,在中, , , 把分成三个全等三角形,并说明理由.聪明的亮亮经过思考后很快就有了思路:作线段的垂直平分线,得到两条相等线段,从而构造出全等三角形,使问题得到了解决.请根据亮亮的思路完成下面的作图并填空
21. 计算:(1)、;(2)、22. 在学习三角形的过程中,亮亮遇到这样一个问题:如图,在中, , , 把分成三个全等三角形,并说明理由.聪明的亮亮经过思考后很快就有了思路:作线段的垂直平分线,得到两条相等线段,从而构造出全等三角形,使问题得到了解决.请根据亮亮的思路完成下面的作图并填空解:用直尺和圆规作的垂直平分线,分别交 , 于点D,E,连接 .
(不写作法,不下结论,只保留作图痕迹)

∵垂直平分线段 ,
∴BE= ▲ , .
在和中,∵ ,
∴ . ∴ ▲ .
∵在中, , ,
∴ ▲ ° .
∴ ▲ ° .
∴ .
在和中,∵ ,
∴ .
∴ .
23. 2022年我国已成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势,经过对A款电动汽车和B款燃油车的对比调查发现,A款电动车汽车平均每千米的充电费比B款燃油车平均每千米的加油费少0.6元.(1)、若充电费和加油费均为200元时,A款电动汽车可行驶的总路程是B款燃油车的4倍,求A款电动汽车平均每千米的充电费;(2)、A款电动车汽车从甲地出发,计划按照一定的速度匀速行驶150km的路程到达乙地.行驶了后,到了一段平坦且车少的路段,决定在原来速度的基础上每小时增加15km,这样,到达乙地所用的总的时间是原计划时间的 , 求原计划的速度.24. 在中, , . D是射线上一点,连接 , 把绕着点A逆时针旋转 , 得到 . (1)、如图1,当点D在的延长线上时,连接 , 求证:;(2)、如图2,当点D在边上时,若 , 过点E作 , 分别交 , , 于点F,M,N.求证: .25. 某学校开展数学实验活动,需要购买A、B两种实验器材.已知购进5套A种实验器材和10套B种实验器材共需1750元;购进10套A种实验器材和15套B种实验器材共需3000元.(1)、求购进一套A种实验器材和一套B种实验器材各需多少元?(2)、若学校购买A种实验器材不少于20套,购买A、B两种实验器材共45套所花费用不超过5600元,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?26. 已知,是的中线,过点C作 .
(1)、如图1,当点D在的延长线上时,连接 , 求证:;(2)、如图2,当点D在边上时,若 , 过点E作 , 分别交 , , 于点F,M,N.求证: .25. 某学校开展数学实验活动,需要购买A、B两种实验器材.已知购进5套A种实验器材和10套B种实验器材共需1750元;购进10套A种实验器材和15套B种实验器材共需3000元.(1)、求购进一套A种实验器材和一套B种实验器材各需多少元?(2)、若学校购买A种实验器材不少于20套,购买A、B两种实验器材共45套所花费用不超过5600元,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?26. 已知,是的中线,过点C作 . (1)、如图1,交于点F,连接 . 求证:四边形是平行四边形;(2)、P是线段上一点(不与点A,D重合),交于点F,交于点E,连接 .
(1)、如图1,交于点F,连接 . 求证:四边形是平行四边形;(2)、P是线段上一点(不与点A,D重合),交于点F,交于点E,连接 .①如图2,四边形是平行四边形吗?请说明理由.
②如图3,延长交于点Q,若 , , ,请直接写出的值.