重庆市开州区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{7}$ D、 $\sqrt{0.5}$

查看试题解析
2. 某校八年级有15名同学参加50米竞赛，预赛成绩各不相同，要取前7名参加决赛，小明已经知道了自己的成绩，他想知道自己能否进入决赛，还需要知道这15名同学成绩的（）

A、中位数 B、众数 C、平均数 D、极差

查看试题解析
3. 若以下列数组成边长，能构成直角三角形的是（）

A、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$ B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ C、4，5，6 D、 $0.2$ ， $0.3$ ， $0.5$

查看试题解析
4. 小文要去参观博物馆，他骑车从家出发，途中因故耽误了一会儿后他又继续骑行，3小时后到达博物馆．小文离家的距离y（单位： $k m$ ）与出发的时间t（单位：h）之间的关系如图所示．下列说法错误的是（）

A、小文两次骑行的速度没有发生变化 B、小文家距博物馆 $15 k m$ C、小文骑行途中因故耽误的时间为 $1 h$ D、小文从家到博物馆共用时 $3 h$

查看试题解析
5. 一次函数 $y = \frac{1}{2} x - 1$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 估计 $\sqrt{3} \times \sqrt{6} - 1$ 的运算结果应在（）

A、2到3 B、3到4 C、4到5 D、5到6

查看试题解析
7. 下列命题是真命题的是（）

A、平行四边形的对角线平分每一组对角 B、两条对角线垂直的四边形是菱形 C、两条对角线相等的菱形是正方形 D、三个角相等的四边形是矩形

查看试题解析
8. 如图矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $C E ∥ B D$ ， $D E ∥ A C$ ，若 $B D = 4$ ，则四边形 $C O D E$ 的周长是（）

A、4 B、6 C、8 D、10

查看试题解析
9. 如图，以直角三角形 $A B C$ 的斜边 $A B$ 为边在三角形 $A B C$ 的同侧作正方形 $A B D E$ ，正方形的对角线 $A D$ ， $B E$ 相交于点 $O$ ，连接 $C O$ ，如果 $A C = 1$ ， $C O = 2 \sqrt{2}$ ，则正方形 $A B D E$ 的面积为（）

A、20 B、22 C、24 D、26

查看试题解析
10. 绝对值的几何意义：一个数的绝对值在数轴上表示这个数的点到原点的距离．若点A、 $B$ 在数轴上表示的数为 $a$ 、 $b$ ，则A、 $B$ 两点之间的距离 $A B = | a - b |$ ，给出下列说法：
①若 $A B = 4$ ，点A表示的数是1，则点 $B$ 表示的数是5；②当 $x = 1$ 时，代数式 $| x + 1 | + | x - 1 | + | x - 2 |$ 的最小值为3；③若 $m$ 、 $n$ 、 $p$ 满足 $(| m | + | 2 + m |) (| - 1 + n | + | - 4 + n |) (| - p - 1 | + | p + 5 |) = 24$ ，则 $m + n + 2 p$ 的最小值为2.以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 在函数 $y = \sqrt{2 x + 3}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
12. 已知一次函数 $y = - 2 x + 1$ 的图象经过 $A (x_{1} ， - 1)$ ， $B (x_{2} ， 1)$ ，则 $x_{1}$ $x_{2}$ （填“＞”“＜”或“＝”）．

查看试题解析
13. 如图是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中 $A E = 5$ ， $A B = 13$ ，则 $E F$ 的值是．

查看试题解析
14. 如图，在菱形 $A B C D$ 中， $E$ 、 $F$ 分别是 $A B$ 、 $C D$ 上的点，且 $A E = C F$ ， $E F$ 与 $A C$ 相交于点 $O$ ，连接 $D O$ ．若 $∠ B A C = 37 °$ ，则 $∠ O D C$ 的度数为．

查看试题解析
15. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x - 1$ 向上平移2个单位长度后与矩形 $O A B C$ 的两边相交，已知 $O A = 3$ ， $O C = 4$ ，则平移后的直线与矩形围成的三角形面积为．

查看试题解析
16. 如图，矩形 $A B C D$ 的边 $B C$ 、 $A D$ 上有两点 $E$ 、 $F$ ，沿着直线 $E F$ 折叠使得点 $D$ 、 $C$ 分别落在 $D^{'}$ 、 $C^{'}$ ， $D^{^{'}} C^{^{'}}$ 交线段 $A D$ 于点 $G$ ，射线 $D^{^{'}} C^{^{'}}$ 恰好经过点 $B$ ，作 $B H$ 平分 $∠ A B G$ 交 $A D$ 于 $H$ ， $H G = G F$ ，且 $H$ 恰好落在线段 $E C^{'}$ 的延长线上，若 $A B = \sqrt{5}$ ，则 $F$ 到直线 $D^{'} H$ 的距离是．

查看试题解析
17. 关于 $x$ 的分式方程 $\frac{a}{3 - x} - \frac{1 - x}{x - 3} = 4$ 的解为正整数，且关于 $y$ 的不等式组 ${\begin{array}{l} \frac{y - a}{5} \leq 1 \\ \frac{3 y + 2}{2} > 2 y - 1 \end{array}$ 的解集为 $y < 4$ ，则满足条件的所有整数 $a$ 之和为．

查看试题解析
18. 已知一个三位数 $M$ ，如果满足百位上的数字与个位上的数字和是十位上的数字的三倍，则称 $M$ 为“三和数”，最小的“三和数”为，若“三和数” $M$ 的前两位数字组成的两位数与 $M$ 的个位上的数字的和记为 $P (M)$ ；交换 $M$ 的百位数字和十位数字，将这两位数字组成的新两位数与 $M$ 的个位数字的和记为 $Q (M)$ ．当 $2 P (M) + 3 Q (M)$ 能被 $4$ 整除时，符合条件的 $M$ 的最大值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{12} + {(\sqrt{7} + 1)}^{0} + | 3 - \sqrt{3} |$

(2)、 ${(\sqrt{5} - 3)}^{2} - (\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3})$

查看试题解析
20. 已知四边形 $A B C D$ 是平行四边形， $A B < A D$ ．

(1)、利用尺规作图作 $∠ B A D$ 的角平分线交 $B C$ 于点 $E$ ，在 $A D$ 上截取 $A F = A B$ ，连接 $E F$ ；（要求保留作图痕迹，不写作法）；

(2)、求证：四边形 $A B E F$ 是菱形．（请补全下面的证明过程）
证明：∵四边形 $A B C D$ 是平行四边形，

∴ $A D ∥ B C$ ，

∴    ▲         ，

∵ $A E$ 平分 $∠ B A F$ ，

∴ $∠ B A E = ∠ F A E$

∴     ▲         ，

∴ $B A = B E$

又∵ $A B = A F$ ，

∴    ▲         ，

又∵    ▲         ，

∴四边形 $A B E F$ 为平行四边形，

又∵    ▲         ，

∴四边形 $A B E F$ 是菱形．

查看试题解析

21. 今年的4月15日是第八个全民国家安全教育日．今年的活动主题是“贯彻总体国家安全观，增强全民国家安全意识和素养，夯实以新安全格局保障新发展格局的社会基础”．某中学开展了国家安全知识竞赛，现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分为整数，并用

x

表示，共分成四组：A．

60 \leq x \leq 70

；B．

70 < x \leq 80

；C．

80 < x \leq 90

；D．

90 < x \leq 100

），下面给出了部分信息：

七年级10名学生的竞赛成绩是：75，69，82，88，92，73，93，81，82，95

八年级10名学生的竞赛成绩分布如扇形图所示，其中在C组的数据是：86，83，89

七、八年级抽取的学生竞赛成绩统计表

年级	平均数	中位数	众数
七年级	83	82	$b$
八年级	83	$a$	95

(1)、直接写出：

a =

，

b =

，

m =

；

(2)、根据图表中的数据，判断七、八年级中哪个年级学生的竞赛成绩更好？请说明理由（写一条理由）；

(3)、若七年级有700人，八年级有800人参与竞赛，请估计七年级和八年级成绩在90分及以上的约有多少人？

查看试题解析

22. 如图，在△ABC中，AB＝AC ，点D、E分别是线段BC、AD的中点，过点A作BC的平行线交BE的延长线于点F ，连接CF ．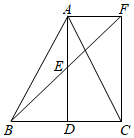

(1)、求证：△BDE≌△FAE；

(2)、求证：四边形ADCF为矩形．

查看试题解析
23. 夏季来临，某批发商决定购进一批防晒产品来销售，批发商分别用 $2000$ 元购进了遮阳帽，用 $3000$ 元购进了太阳伞，两款产品的数量一样，其中太阳伞的单价比遮阳帽贵 $5$ 元．

(1)、遮阳帽的单价为多少元；

(2)、由于畅销，该批发商决定再购进这两款产品共 $750$ 件，其中购进太阳伞的数量不少于遮阳帽的 $2$ 倍，销售时，售价均定为 $20$ 元每件，那么该批发商需购进这两款产品各多少件才能使利润最大，最大利润为多少？

查看试题解析
24. 如图，在正方形 $A B C D$ 中， $A B = 4$ ，动点 $P$ 从点 $A$ 出发，沿 $A \to D \to C \to B$ 以每秒1个单位的速度运动，到达点 $B$ 停止运动，连接 $B P$ ，设点 $P$ 的运动时间为 $x (s)$ ， $△ A B P$ 的面积为 $y$ （当点 $P$ 与 $A$ 、 $B$ 两点重合时， $y$ 的值为0）

(1)、直接写出 $y$ 与 $x$ 的函数关系式，并写出自变量 $x$ 的取值范围；

(2)、在给出的平面直角坐标系中，画出函数图象，并写出这个函数的一条性质 ▲ ；

(3)、根据函数图象直接写出不等式 $y \leq 5$ 的解集是．

查看试题解析
25. 如图，在平面直角坐标系中，一次函数 $y = \frac{2}{3} x + 2$ 的图象与 $x$ 轴， $y$ 轴分别交于 $A$ 、 $B$ 两点，以 $A B$ 为边在第二象限内作等腰 $R t △ A B C$ ， $∠ B A C = 90 °$ ．

(1)、求 $△ A B C$ 的面积；

(2)、求直线 $B C$ 的解析式；

(3)、点 $N$ 为线段 $A B$ 上一动点，过点 $N$ 作 $M N ∥ y$ 轴交 $B C$ 于点 $M$ ，当 $M N = \frac{1}{2} O B$ 时，求四边形 $A N M C$ 的面积及此时点 $M$ 的坐标．

查看试题解析
26. 在平行四边形 $A B C D$ 中，点 $E$ 在平行四边形 $A B C D$ 内，连接 $E C$ ， $E D$ ， $E B$ ， $△ E C D$ 是等腰直角三角形， $∠ E C D = 90 °$ ，其中 $E B = E C$ ．

(1)、如图1，求 $∠ D A E$ 的度数；

(2)、如图2，在 $B C$ 上取点 $F$ ，使得 $A B = A F$ ，求证： $\sqrt{2} A E + B F = A D$ ；

(3)、如图3，在2问的条件下，若 $B$ 、 $E$ 、 $D$ 在同一直线上，当 $A E = \sqrt{2}$ 时，求平行四边形 $A B C D$ 的面积．

查看试题解析