重庆市合川区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 某初中学生一周内连续6天课外阅读的时间分别为:0.8,0.8,0.8,0.9,0.9,1(单位:小时),则这组数据的中位数为( )A、1 B、0.9 C、0.85 D、0.82. 若二次根式有意义,则的取值范围是( ).A、 B、 C、 D、3. 下列各组数中,是勾股数的是( )A、1,2,3 B、6,7,8 C、6,8,10 D、9,40,424. 张开大拇指和中指,两端的距离为“一拃”,据统计,通常情况下,人的一拃长单位:厘米与本人的身高单位:厘米之间的关系为: , 则下列关于变量和常量的说法正确的是( )
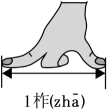 A、是变量,是常量 B、是变量,是常量 C、与是变量,与是常量 D、与是变量,与是常量5. 一次实心球训练,甲、乙、丙三名同学各进行了十次抛掷,每人抛掷距离的平均数均为米,甲的方差为3,乙的方差为10,丙的方差为 , 这3名同学实心球抛掷的成绩最稳定的是( )A、甲 B、乙 C、丙 D、无法确定6. 估计的值应在( )A、0到1之间 B、1到2之间 C、2到3之间 D、3到4之间7. 如图,在菱形中,过点C作的垂线与的平分线交于点E,若 , 则的度数为( )
A、是变量,是常量 B、是变量,是常量 C、与是变量,与是常量 D、与是变量,与是常量5. 一次实心球训练,甲、乙、丙三名同学各进行了十次抛掷,每人抛掷距离的平均数均为米,甲的方差为3,乙的方差为10,丙的方差为 , 这3名同学实心球抛掷的成绩最稳定的是( )A、甲 B、乙 C、丙 D、无法确定6. 估计的值应在( )A、0到1之间 B、1到2之间 C、2到3之间 D、3到4之间7. 如图,在菱形中,过点C作的垂线与的平分线交于点E,若 , 则的度数为( )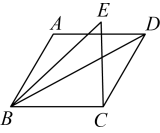 A、 B、 C、 D、8. 如图,在四边形中, , , , 则的度数为( )
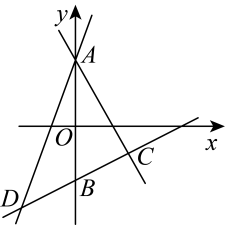
A、 B、 C、 D、8. 如图,在四边形中, , , , 则的度数为( )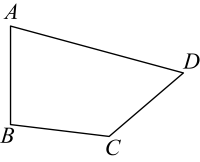 A、 B、 C、 D、9. 如图,一次函数的图象分别与x轴,y轴的正半轴交于点A、B,为该图象上不重合的两点,则下列结论中:①;②若 , 则;③当时, . 正确结论的个数为( )
A、 B、 C、 D、9. 如图,一次函数的图象分别与x轴,y轴的正半轴交于点A、B,为该图象上不重合的两点,则下列结论中:①;②若 , 则;③当时, . 正确结论的个数为( )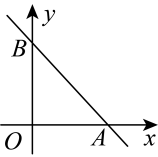 A、0 B、1 C、2 D、310. 如图,在矩形中, , 为的中点,连接 , 将沿所在直线翻折至四边形所在平面内,得 , 延长与交于点 , 若 , 则四边形的面积为( )
A、0 B、1 C、2 D、310. 如图,在矩形中, , 为的中点,连接 , 将沿所在直线翻折至四边形所在平面内,得 , 延长与交于点 , 若 , 则四边形的面积为( )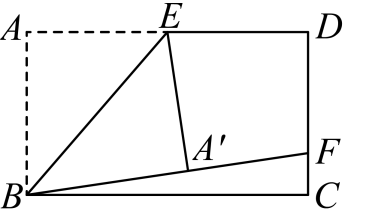 A、 B、8 C、12 D、16
A、 B、8 C、12 D、16二、填空题
-
11. 我区某个月连续5天中午12时的气温(单位:℃)为:26,28,29,29,28.则这5天中午12时的平均气温为℃.(结果取整数)12. 将直线 向上平移3个单位长度,所得直线的解析式为.13. 如图,直线 ,的直角顶点在直线上,点在直线上,若边的中点在直线上且 , 则的度数为 .
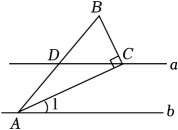 14. 已知 , 代数式的值为 .15. 如图,在中, , 是边上的中线,若 , , 则的长度为 .
14. 已知 , 代数式的值为 .15. 如图,在中, , 是边上的中线,若 , , 则的长度为 .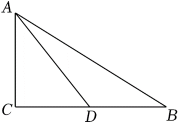 16. 在平面直角坐标系中,若一次函数的图象经过二、三、四象限,则m的取值范围为 .17. 如图,在正方形中,分别为的中点,与交于点为的中点,连接 , 若 , 则的长度为 .
16. 在平面直角坐标系中,若一次函数的图象经过二、三、四象限,则m的取值范围为 .17. 如图,在正方形中,分别为的中点,与交于点为的中点,连接 , 若 , 则的长度为 .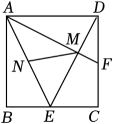 18. 对于一个四位数 , 若其千位上的数字与十位上的数字之和等于百位上的数字与个位上的数字之和,则称数为“等合数”.例如:数3465,∵3 , ∴3465是“等合数”,数2364,∵ , , ∴ , ∴2364不是“等合数”,则最大的“等合数”为 ;若“等合数”各个数位上的数字互不相同且均不为零,将其千位上的数字与个位上的数字对调,百位上的数字与十位上的数字对调,组成一个新的四位数记为 , 若 为完全平方数,则满足条件的的最小值为 .
18. 对于一个四位数 , 若其千位上的数字与十位上的数字之和等于百位上的数字与个位上的数字之和,则称数为“等合数”.例如:数3465,∵3 , ∴3465是“等合数”,数2364,∵ , , ∴ , ∴2364不是“等合数”,则最大的“等合数”为 ;若“等合数”各个数位上的数字互不相同且均不为零,将其千位上的数字与个位上的数字对调,百位上的数字与十位上的数字对调,组成一个新的四位数记为 , 若 为完全平方数,则满足条件的的最小值为 .三、解答题
-
19. 计算:(1)、(2)、20. 棉花的纤锥长度是棉花质量的重要指标.在甲、乙两类送检的棉花中各随机抽测了根棉花的纤锥长度(单位:毫米),按从小到大排序结果如下:
甲: , , , , , , , , , , , , , , , , , , , .
乙: , , , , , , , , , , , , , , , , , , , .
根据以上数据绘制成统计表:
名称
平均数
众数
中位数
方差
甲
乙
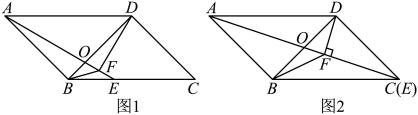
(1)、填空:;;(2)、若甲类棉花共有根,试估计甲类棉花的纤维长度不低于毫米的数量;(3)、抽检员看了数据及统计表后认为甲类棉花纤维长度的稳定性更好,请结合所学知识和统计数据,写出支持检测员的结论的依据.21. 一次函数的图象经过 , 两点.(1)、求的值;(2)、求该一次函数图象与轴的交点坐标;(3)、判断点 , 是否在该一次函数图象上.22. 如图,在等腰三角形中,底边 , D是上一点,连接 .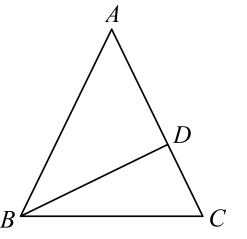 (1)、求证:是直角三角形;(2)、求边的长度.23. 如图,在平行四边形中,为对角线的中点,过点的直线分别与 , 的延长线交于点 , , 分别与 , 交于点 , .
(1)、求证:是直角三角形;(2)、求边的长度.23. 如图,在平行四边形中,为对角线的中点,过点的直线分别与 , 的延长线交于点 , , 分别与 , 交于点 , .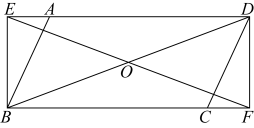 (1)、求证:F;(2)、若 , 判断四边形的形状,并说明理由.24. 学校决定按年级开展师生研学活动,该校八年级师生共580人将参加研学活动,计划租用12辆大客车,现有甲、乙两种型号的大客车,它们的满座载客量和租车费用如下表:
(1)、求证:F;(2)、若 , 判断四边形的形状,并说明理由.24. 学校决定按年级开展师生研学活动,该校八年级师生共580人将参加研学活动,计划租用12辆大客车,现有甲、乙两种型号的大客车,它们的满座载客量和租车费用如下表:甲型号大客车
乙型号大客车
满座载客量(人/辆)
55
35
租车费用(元/辆)
1200
800
(1)、若租用的12辆大客车恰好能一次将八年级师生送到研学基地,求应分别租用甲、乙型号的大客车多少辆?(2)、设租用甲型号大客车x辆,租车总费用为y元.①求出y(元)与x(辆)的函数关系式,并求出x的取值范围;
②当租用甲型号大客车多少辆时,租车的总费用最少,最少费用是多少?