山西省阳泉市2022-2023学年八年级下学期6月期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,能构成直角三角形的一组是( )A、1,2,3 B、1,1, C、2,3,4 D、7,15,173. 矩形、菱形、正方形都具有的性质是( ).A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角4. 我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.下列四幅图中,不能证明勾股定理的是( )A、
 B、
B、 C、
C、 D、
D、 5. 将一次函数的图象向上平移2个单位长度后所对应的函数解析式为( )A、 B、 C、 D、6. 在日常生活中,对某些技能的训练,新手的表现通常不太稳定.以下是四名学生进行8次射击训练之后的成绩统计图,请根据图中信息估计最可能是新手的是( )A、
5. 将一次函数的图象向上平移2个单位长度后所对应的函数解析式为( )A、 B、 C、 D、6. 在日常生活中,对某些技能的训练,新手的表现通常不太稳定.以下是四名学生进行8次射击训练之后的成绩统计图,请根据图中信息估计最可能是新手的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )
7. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )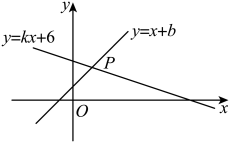 A、 B、 C、 D、8. 如图,在中,对角线AC,BD相交于点O.若 , , , 则的长为( )
A、 B、 C、 D、8. 如图,在中,对角线AC,BD相交于点O.若 , , , 则的长为( )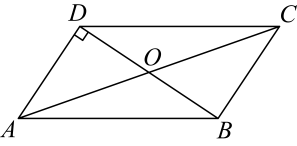 A、8 B、9 C、10 D、129. 硫酸钠()是一种主要的日用化工原料,主要用于制造洗涤剂和牛皮纸制浆工艺.硫酸钠的溶解度y()与温度t()之间的对应关系如图所示,则下列说法正确的是( )
A、8 B、9 C、10 D、129. 硫酸钠()是一种主要的日用化工原料,主要用于制造洗涤剂和牛皮纸制浆工艺.硫酸钠的溶解度y()与温度t()之间的对应关系如图所示,则下列说法正确的是( )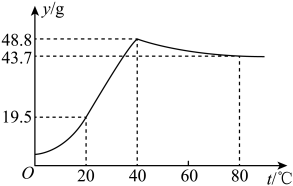 A、当温度为时,硫酸钠的溶解度为 B、硫酸钠的溶解度随着温度的升高而增大 C、当温度为时,硫酸钠的溶解度最大 D、要使硫酸钠的溶解度大于 , 温度只能控制在10. 如图,在菱形中, , . 若E,F,G,H分别是边 , , , 的中点,连接 , , , , 则图中阴影部分的面积为( )
A、当温度为时,硫酸钠的溶解度为 B、硫酸钠的溶解度随着温度的升高而增大 C、当温度为时,硫酸钠的溶解度最大 D、要使硫酸钠的溶解度大于 , 温度只能控制在10. 如图,在菱形中, , . 若E,F,G,H分别是边 , , , 的中点,连接 , , , , 则图中阴影部分的面积为( ) A、6 B、 C、 D、
A、6 B、 C、 D、二、填空题
-
11. 请写出一个y随着x的增大而减小的正比例函数解析式 .12. 如图,平行四边形的顶点 , , 的坐标分别为 , , , 则顶点的坐标为 .
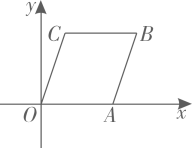 13. 如图,在中,对角线 , 相交于点O,点E,F在上,且 , 连接 , , , . 若添加一个条件使四边形是矩形,则该条件可以是 . (填写一个即可)
13. 如图,在中,对角线 , 相交于点O,点E,F在上,且 , 连接 , , , . 若添加一个条件使四边形是矩形,则该条件可以是 . (填写一个即可)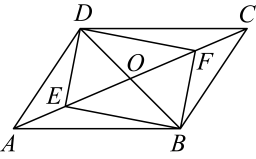 14. 我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离 的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为.
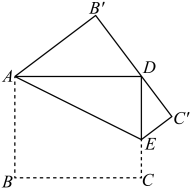
14. 我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离 的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为. 15. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
15. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
三、解答题
-
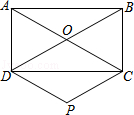
16. 计算:(1)、;(2)、 .17. 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线相交于点P,求证:四边形CODP是菱形.
 18. 《国务院关于印发全民健身计划(2021-2025年)的通知》文件提出,加大全民健身场地设施供给,建立健全场馆运营管理机制,提升场馆使用效益.某健身中心为答谢新老顾客举行夏日大回馈活动,特推出两种“夏季唤醒计划”活动方案.
18. 《国务院关于印发全民健身计划(2021-2025年)的通知》文件提出,加大全民健身场地设施供给,建立健全场馆运营管理机制,提升场馆使用效益.某健身中心为答谢新老顾客举行夏日大回馈活动,特推出两种“夏季唤醒计划”活动方案.方案1:顾客不购买会员卡,每次健身收费40元.
方案2:顾客花200元购买会员卡,每张会员卡仅限本人使用一年,每次健身收费15元.
设小宇一年内来此健身中心健身的次数为x(次),选择方案1的费用为(元),选择方案2的费用为(元).
(1)、请直接写出 , 与x之间的函数关系式.(2)、当小宇一年内来此健身中心健身的次数在什么范围时,选择方案2所需费用较少?并说明理由.19. 2023年3月5日,中华人民共和国第十四届全国人民代表大会第一次会议在北京召开,某校为使学生更好地了解“两会”,争做新时代好少年,开展了“两会”知识竞赛活动,分别从八(1)班和八(2)班各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并对数据进行了如下分析与整理:收集数据
八(1)班学生知识竞赛成绩:84,75,82,70,91,83,80,74,79,82
八(2)班学生知识竞赛成绩:80,65,75,68,95,82,84,80,92,79
分析数据
平均数/分
中位数/分
众数/分
方差
八(1)班
80
b
82
31.6
八(2)班
a
80
c
78.4
根据以上信息,解答下列问题:
(1)、填空: , , .(2)、请你对八(1)班和八(2)班抽取的这10名学生的知识竞赛成绩作出评价.(3)、该校除开展两会知识竞赛活动外,还组织了制作关于“两会”手抄报的评比活动,并对手抄报进行评分(单位:分,满分100分).在八(2)班抽取的这10名学生中,甲同学和乙同学的知识竞赛成绩分别为95分和92分,手抄报成绩分别为70分和80分.现对甲同学和乙同学进行综合评分,若知识竞赛成绩占70%,手抄报成绩占30%,则哪位同学的综合成绩较好?20. 如图,某火车站内部墙面上有破损处(看作点A),现维修师傅需借助梯子完成维修工作.梯子的长度为 , 将其斜靠在这面墙上,测得梯子底部E离墙角N处 , 维修师傅爬到梯子顶部使用仪器测量,此时梯子顶部D距离墙面破损处 . (1)、该火车站墙面破损处A距离地面有多高?(2)、如果维修师傅要使梯子顶部到地面的距离为4.8m.那么梯子底部需要向墙角方向移动多少米?21. 阅读与思考:在函数的学习过程中,我们利用描点法画出函数的图象,并借助图象研究该函数的性质,最后运用函数解决问题.现我们对函数y=|x-1|(x的取值范围为任意实数)进行探究.
(1)、该火车站墙面破损处A距离地面有多高?(2)、如果维修师傅要使梯子顶部到地面的距离为4.8m.那么梯子底部需要向墙角方向移动多少米?21. 阅读与思考:在函数的学习过程中,我们利用描点法画出函数的图象,并借助图象研究该函数的性质,最后运用函数解决问题.现我们对函数y=|x-1|(x的取值范围为任意实数)进行探究.x
…
0
1
2
3
…
y=|x-1|
…
4
▲
2
1
0
▲
2
…
⑴请将上面的表格补充完整.
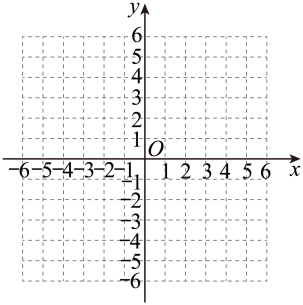
⑵请根据上表中的数据,在如图所示的平面直角坐标系中画出这个函数的图象,并回答:当时,y的值随x值的增大而 ▲ .
⑶请在如图所示的平面直角坐标系中画出正比例函数的图象,并直接写出不等式的解集.
22. 综合与实践(1)、问题情境:
在综合实践活动课上,同学们以“平行四边形纸片的折叠”为主题开展数学活动.在平行四边形纸片中,E为边上任意一点,将沿折叠,点D的对应点为 .

分析探究:
如图1,当点恰好落在边上时,四边形的形状为 .(2)、问题解决:
如图2,当E,F为边的三等分点时,连接并延长,交边于点G.试判断线段与的数量关系,并说明理由.(3)、如图3,当 , 时,连接并延长,交边于点H.若的面积为24, , 请直接写出线段的长.23. 综合与探究:如图1,在平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与x轴交于点C. (1)、直接写出k,b,m的值.(2)、如图2,P是y轴负半轴上一动点,过点P作y轴的垂线,分别交直线 , 于点D,E,连接 . 设点P的坐标为 .
(1)、直接写出k,b,m的值.(2)、如图2,P是y轴负半轴上一动点,过点P作y轴的垂线,分别交直线 , 于点D,E,连接 . 设点P的坐标为 .①点D的坐标为 , 点E的坐标为;(用含n的代数式表示)
②当时,求点P的坐标.
(3)、在(2)的条件下,线段上是否存在点Q,使?若存在,请直接写出点Q的坐标;若不存在,请说明理由.