山西省朔州市应县2022-2023学年八年级下学期7月期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 9的平方根是( )A、3 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 一次函数的图象与y轴交点的坐标是( )A、 B、 C、 D、4. 对于函数 , 下列说法正确的是( )A、当时,y随x的增大而减小 B、当时,y随x的增大而减小 C、y随x的增大而减小 D、y随x的增大而增大5. 如图,四边形为矩形,对角线与交于点O,以下说法不一定正确的是( )
 A、 B、 C、 D、6. 如图Rt△ABC中,∠BAC=90°,分别以边AB,CA,BC向外作正方形,正方形ABIH的面积为25,正方形BDEC的面积为169,则正方形ACFG的面积是( )
A、 B、 C、 D、6. 如图Rt△ABC中,∠BAC=90°,分别以边AB,CA,BC向外作正方形,正方形ABIH的面积为25,正方形BDEC的面积为169,则正方形ACFG的面积是( ) A、194 B、144 C、122 D、1107. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数(单位:分)及方差如表所示:如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
A、194 B、144 C、122 D、1107. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数(单位:分)及方差如表所示:如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )甲
乙
丙
丁
平均数
7
8
8
7
方差
1
1
1.2
1.8
A、甲 B、乙 C、丙 D、丁8. 如图,在平面直角坐标系中,直线l1: 与直线l2: 交于点A( ,b),则关于x、y的方程组 的解为( )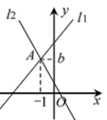 A、 B、 C、 D、9. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )
A、 B、 C、 D、9. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )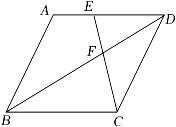 A、16 B、6 C、12 D、3010. 如图,在 中, 两顶点 在 轴、 轴上滑动,点 在第一象限内,连接 ,则 的最大值为( )
A、16 B、6 C、12 D、3010. 如图,在 中, 两顶点 在 轴、 轴上滑动,点 在第一象限内,连接 ,则 的最大值为( )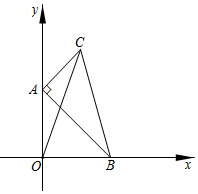 A、7 B、8 C、9 D、
A、7 B、8 C、9 D、二、填空题
-
11. 下表是某校女子排球队队员的年龄分布.
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员年龄的众数是 .
12. 已知是整数,则正整数的最小值为 .13. 如图,一棵树在一次强台风中在离地面米处折断倒下,倒下部分与地面成的夹角,树尖离树根的水平距离是米,则 .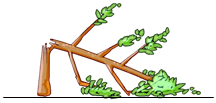 14. 如图,正方形中,点E是对角线上的一点,且 , 连接 , , 则的度数为 .
14. 如图,正方形中,点E是对角线上的一点,且 , 连接 , , 则的度数为 . 15. 勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”. 图②由弦图变化得到,它是由八个全等的直角三角形拼接而成. 记图中正方形、正方形、正方形的面积分别为 . 若 , 则正方形的边长为 .
15. 勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”. 图②由弦图变化得到,它是由八个全等的直角三角形拼接而成. 记图中正方形、正方形、正方形的面积分别为 . 若 , 则正方形的边长为 .
三、解答题
-
16. 计算:(1)、 .(2)、 .17. 在边长为1的小正方形组成的方格纸中,若三角形的各顶点都在方格的格点(横竖格子线的交错点)上,这样的三角形称为格点三角形.
 (1)、请在图甲中画一个格点三角形,使是一个等腰直角三角形,并求出的面积.(2)、请在图乙中仅用无刻度的直尺 , 画出的平分线(保留作图痕迹).18. 如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的时间与路程图象如图所示,请根据图象回答下列问题:
(1)、请在图甲中画一个格点三角形,使是一个等腰直角三角形,并求出的面积.(2)、请在图乙中仅用无刻度的直尺 , 画出的平分线(保留作图痕迹).18. 如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的时间与路程图象如图所示,请根据图象回答下列问题: (1)、先出发,提前小时;(2)、运动过程中甲的速度为:千米/小时,乙的速度为:千米/小时;(3)、请直接写出在甲的行进过程中,当甲、乙两人相距15千米时,自变量x的值是多少?19. 如图,在平行四边形中,对角线相交于点O,点E,F在上, , 连接 .
(1)、先出发,提前小时;(2)、运动过程中甲的速度为:千米/小时,乙的速度为:千米/小时;(3)、请直接写出在甲的行进过程中,当甲、乙两人相距15千米时,自变量x的值是多少?19. 如图,在平行四边形中,对角线相交于点O,点E,F在上, , 连接 . (1)、求证:四边形为平行四边形;(2)、若 , 求证:四边形是矩形.20. 甲、乙两位同学参加数学质量测试活动,各项成绩如下(单位:分)
(1)、求证:四边形为平行四边形;(2)、若 , 求证:四边形是矩形.20. 甲、乙两位同学参加数学质量测试活动,各项成绩如下(单位:分)数与代数
空间与图形
统计与概率
综合与实践
学生甲
学生乙
(1)、学生甲成绩的中位数是 , 学生乙成绩的众数是;(2)、如果将“数与代数”“ 空间与图形”“ 统计与概率”“ 综合与实践”四项成绩按3:3:2:2的比例确定最终成绩,通过计算说明学生甲、乙谁的成绩较高.21. 如图,在中, , 点D在边上且 , 连接 , E是的中点,过点C作 , 交的延长线于点F,连接 . (1)、求证:;(2)、求证:四边形是菱形.22. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)、求证:;(2)、求证:四边形是菱形.22. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
 (1)、①如图2,3,4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,面积分别为 , , , 利用勾股定理,判断这3个图形中面积关系满足的有 ▲ 个.
(1)、①如图2,3,4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,面积分别为 , , , 利用勾股定理,判断这3个图形中面积关系满足的有 ▲ 个.②如图5,分别以直角三角形三边为直径作半圆,设图中两个月牙形图案(图中阴影部分)的面积分别为 , , 直角三角形面积为 , 也满足吗?若满足,请证明;若不满足,请求出 , , 的数量关系.
(2)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图6所示的“勾股树”.在如图7所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,则 .23. 如图,在平面直角坐标系中,过点C(0,6)的直线AB与直线OA相交于点A(4,2),动点M在直线OA和射线AC上运动. (1)、求直线AB的解析式;(2)、求△OAB的面积;(3)、是否存在点M,使△OMC的面积是△OAB的面积的?若存在,求出此时点M的坐标;若不存在,说明理由.
(1)、求直线AB的解析式;(2)、求△OAB的面积;(3)、是否存在点M,使△OMC的面积是△OAB的面积的?若存在,求出此时点M的坐标;若不存在,说明理由.