山西省朔州市2022-2023学年八年级下学期7月期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 若二次根式 有意义,则x的取值范围是( )A、x<5 B、x>5 C、x≤5 D、x≥52. 某区新教师招聘中,九位评委独立给出分数,得到一列数.若去掉一个最高分和一个最低分,得到一列新数,那么这两列数的相关统计量中,一定相等的是( )A、方差 B、众数 C、中位数 D、平均数3. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、4. 对于函数 , 下列结论正确的是( )A、它的图象必经过点 B、它的图象经过第一、二、三象限 C、当时, D、的值随值的增大而增大5. 如图学校门口的伸缩门在伸缩的过程中,会出现不少菱形.某一时刻,测得菱形的对角线 , , 则这个菱形的面积为( )
 A、 B、 C、 D、6. 甲,乙两人在一次百米赛跑中,路程与时间的关系如图所示,下列说法正确的是( )
A、 B、 C、 D、6. 甲,乙两人在一次百米赛跑中,路程与时间的关系如图所示,下列说法正确的是( ) A、乙先到达终点 B、甲比乙晚到秒 C、甲在这次赛跑中的平均速度为8米/秒 D、乙在这次赛跑中的平均速度为8米/秒7. 如图,是四边形的对角线, , 则四边形的面积等于( )
A、乙先到达终点 B、甲比乙晚到秒 C、甲在这次赛跑中的平均速度为8米/秒 D、乙在这次赛跑中的平均速度为8米/秒7. 如图,是四边形的对角线, , 则四边形的面积等于( ) A、 B、 C、 D、8. 如图,中,为边上一点,为边上一点,四边形为矩形,若 , , 则的度数是( )
A、 B、 C、 D、8. 如图,中,为边上一点,为边上一点,四边形为矩形,若 , , 则的度数是( )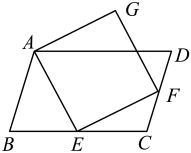 A、 B、 C、 D、9. 如图,在中, , 点分别是边 , 的中点,点是线段上的一点.连接 , , 若 , 且 , , 则的长是( )
A、 B、 C、 D、9. 如图,在中, , 点分别是边 , 的中点,点是线段上的一点.连接 , , 若 , 且 , , 则的长是( )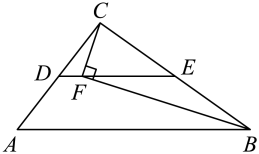 A、 B、1 C、 D、210. 如图,在平面直角坐标系中,矩形的点和点分别落在轴和轴正半轴上, , 直线经过点 , 将直线向下平移个单位,若直线可将矩形的面积平分,则的值为( )
A、 B、1 C、 D、210. 如图,在平面直角坐标系中,矩形的点和点分别落在轴和轴正半轴上, , 直线经过点 , 将直线向下平移个单位,若直线可将矩形的面积平分,则的值为( ) A、11 B、9 C、6 D、5
A、11 B、9 C、6 D、5二、填空题
-
11. 已知长方形的面积为 , 相邻两边分别为 , 已知 , 则的长为 .12. 学校为提升教职工的身体素质,开展了“放飞心情,健行健康”为主题的健步走活动,李老师用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:
步数(万步)
1.1
1.2
1.3
1.4
1.5
天数
2
3
10
12
3
在每天所走的步数这组数据中,众数是万步.
13. 如图,每个小正方形的边长都为 , 的顶点都在小正方形的顶点上,则该三角形的最长边等于 . 14. 如图,一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加 . 根据小球速度(单位:)关于时间(单位:)的函数关系,第时小球的速度为
14. 如图,一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加 . 根据小球速度(单位:)关于时间(单位:)的函数关系,第时小球的速度为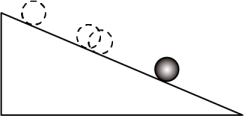 15. 如图,在中, , , 点在边上,于点 , 交于点 . 若 , 则的长为 .
15. 如图,在中, , , 点在边上,于点 , 交于点 . 若 , 则的长为 .
三、解答题
-
16.(1)、计算:;(2)、计算: .17. 如图,四边形中, , 点是的中点, . 求证:四边形是菱形.
 18. 根据山西省教育厅“2023年度基础教育领域重点工作推进会”要求,扎实推进建设100所公办幼儿园任务落实,某地计划要在如图所示的直线上,新建一所幼儿园,该区域有两个小区所在的位置在点和点处,于A,于B.已知 , , 求该幼儿园应该建在距点A为多少处,可以使两个小区到幼儿园的距离相等.
18. 根据山西省教育厅“2023年度基础教育领域重点工作推进会”要求,扎实推进建设100所公办幼儿园任务落实,某地计划要在如图所示的直线上,新建一所幼儿园,该区域有两个小区所在的位置在点和点处,于A,于B.已知 , , 求该幼儿园应该建在距点A为多少处,可以使两个小区到幼儿园的距离相等. 19. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往A,B,C三地销售,要求运往C地的袋数是运往A地袋数的3倍,各地的运费如下表所示:
19. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往A,B,C三地销售,要求运往C地的袋数是运往A地袋数的3倍,各地的运费如下表所示:
运往地
地
地
地
运费(元/袋)
20
10
15
(1)、设运往地的小米(袋),总运费为(元),试写出与的函数关系式;(2)、若总运费不超过15000元,最多可运往A地小米多少袋?20. 学校举办纪念“五四运动”104周年暨“青春心向党,建功新时代”演讲比赛.同学们用青春的声音和故事,激扬五四精神,彰显青春风采,展现拼搏风貌,深情地演绎了对党和祖国的热爱之情.
初赛阶段两个年级各10名选手的成绩统计如下:
七年级:98 96 86 85 84 94 77 69 59 94
八年级:99 96 73 82 96 79 65 96 55 96
他们的数据分析过程如下:
(1)、整理、描述数据:根据上面得到的两组数据,分别绘制频数分布直方图如图:
请补全八年级频数分布直方图;
(2)、数据分析:两组数据的平均数、中位数、方差如表所示:年级
平均数
中位数
方差
七年级
①
85.5
144.36
八年级
83.7
②
251.21
根据以上数据求出表格中①,②两处的数据;
(3)、推断结论:根据以上信息,判断哪个年级比赛成绩整体较好?说明理由(至少从两个不同角度说明判断的合理性).21. 请阅读下列材料,并完成相应的任务:运用“坐标法”解决几何问题
数学知识之间是相互联系的,有些几何问题可以运用“坐标法”解决.其步骤是:首先根据图形特点,在平面上建立坐标系,然后运用函数(或方程)知识研究几何图形,最后把图形性质用几何语言叙述,从而得到原先几何问题的答案.
例题:如图,在中, , 是的角平分线, , , 用你所学的知识求线段的长.
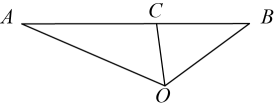
解:如图,以为坐标原点,所在的直线为轴,建立平面直角坐标系.
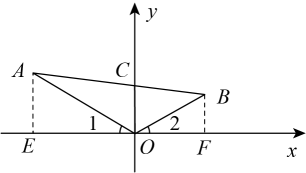
∵ , 是的角平分线,
∴ .
∴
∵ , ,
∴ , , , .
∴ ,
设直线的函数表达式为 .
∴解得 .
∴
∴当时, .
∴线段的长为3.
通过这个问题的解答,我们发现用“坐标法”解决几何问题,关键是根据图形特点,建立适当的坐标系.
任务:请用“坐标法”解答下面问题:
如图,已知正方形中, , 点在的延长线上,且 , 连接 , 相交于点 , 连接交于点 , 求的长.
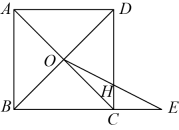 22. 综合与实践:(1)、操作发现:
22. 综合与实践:(1)、操作发现:如图1,在纸片中, , 于点 .
第一步:将一张与其全等的纸片,沿剪开;
第二步:在同一平面内,将所得的两个三角形,和拼在一起.如图2所示,这两个三角形分别记为和;
第三步:分别延长和相交于点 .

求证:四边形是正方形;
(2)、拓广探索:如图3,连接分别交 , 于点 , 在四边形外作 , 使得 , , 判断线段 , , 之间的数量关系,并说明理由.
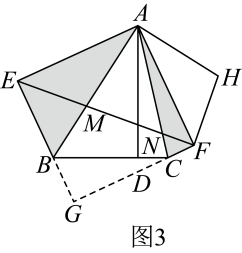 23. 如图,在平面直角坐标系中,点 , 点为正方形的两个顶点,点和在第一象限.
23. 如图,在平面直角坐标系中,点 , 点为正方形的两个顶点,点和在第一象限. (1)、求点的坐标;(2)、求直线的函数表达式;(3)、在直线上是否存在点 , 使为等腰三角形?若存在,请直接写出点的坐标;若不存在,说明理由.
(1)、求点的坐标;(2)、求直线的函数表达式;(3)、在直线上是否存在点 , 使为等腰三角形?若存在,请直接写出点的坐标;若不存在,说明理由.