山西省太原市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 分式 $\frac{x + 1}{x - 2}$ 有意义的条件是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \neq 2$ D、 $x \neq - 1$

查看试题解析
2. 电动车在我国发展已经超过30年时间，在两轮电动车领域，不断有科技含量高的技术出现．下列电动车新技术的图标中，文字上方的图案既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列多项式中，能用平方差公式分解因式的是（）

A、 $x^{2} - 4 x$ B、 $x^{2} - 4 x + 4$ C、 $x^{2} - 4$ D、 $x^{2} + 4$

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $A B = 5$ ，点 $D$ ， $E$ 分别是 $A C$ ， $A B$ 的中点，则 $D E$ 的长为（）

A、1.5 B、2 C、2.5 D、4

查看试题解析
5. 要将 $\frac{5 x y z}{20 x^{2} y}$ 化成最简分式，应将分子分母同时约去它们的公因式，这个公因式为（）

A、 $x y$ B、 $5 x y$ C、 $5 x y z$ D、 $20 x y$

查看试题解析
6. 不等式 $2 - 3 x > 2 x - 8$ 的正整数解有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A B ⊥ B D$ ， $∠ A O B = 45 °$ ．若 $B D = 4$ ，则 $A C$ 的长为（）

A、8 B、 $2 \sqrt{2}$ C、2 D、 $4 \sqrt{2}$

查看试题解析
8. 已知一个圆的面积为 $9 π a^{2} + 6 π a b + π b^{2} (a > 0 ， b > 0)$ ，则该圆的半径是（）

A、 $3 a + b$ B、 $9 a + b$ C、 $3 a b$ D、 $3 π a + π b$

查看试题解析
9. 如图，正五边形 $A B C D E$ 中，边 $A E$ ， $C D$ 的延长线交于点 $F$ ，则 $∠ F$ 的度数为（）

A、 $30 °$ B、 $32 °$ C、 $36 °$ D、 $72 °$

查看试题解析
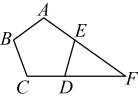10. 某种型号油电混合动力汽车从甲地开往乙地时，纯用电行驶，花充电费24元，沿相同路线返程时用纯燃油行驶，花燃油费72元．已知每行驶1千米，纯燃油费用比纯用电费用多0.6元．晓华根据这一情境中的数量关系列出方程 $\frac{24}{x} = \frac{72}{x + 0.6}$ ，则未知数 $x$ 表示的意义为（）

A、每行驶1千米纯用电的费用 B、每行驶1千米纯燃油的费用 C、每1元电费可行驶的路程 D、每1元邮费可行驶的路程

查看试题解析

二、填空题

11. 在平面直角坐标系中，点A $(- 2 ， 3)$ 关于原点O成中心对称的点的坐标为．

查看试题解析
12. 多项式“ $3 m^{3} - 5 m^{2} + ▲$ ”分解因式的结果为 $m (3 m^{2} - 5 m - 2)$ ，则原多项式中“ $▲$ ”处所缺的项为．

查看试题解析
13. 如图，将 $△ A B C$ 沿射线 $B C$ 方向平移，当点 $B$ 的对应点与点 $C$ 重合时得到 $△ D C E$ ，连接 $A D$ ，若 $∠ A C B = 80 °$ ，则 $∠ A D E$ 的度数为．

查看试题解析
14. 如图，直线 $y = a x + b (a \neq 0)$ 过点 $A (- 3 ， 0)$ ， $B (0 ， 3)$ ，则关于 $x$ 的不等式 $a x + b > 3$ 的解集是．

查看试题解析
15. 已知，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 是 $A C$ 的中点， $D E ⊥ A B$ 于点 $E$ ，连接 $C E$ 请从下面A，B两题中任选一题作答．我选择．
A．如图1，若 $A C = B C = 8$ ，则线段 $C E$ 的长为．
B．如图2，若 $A C = 8$ ， $B C = 6$ ，则线段 $C E$ 的长为．

查看试题解析

三、解答题

16. 分解因式：

(1)、 $x^{3} y - 9 y$ ；

(2)、 $(a + 1) (a - 1) - {(1 + a)}^{2}$ ；

(3)、利用因式分解计算： $8 4^{2} - 28 \times 84 + 1 4^{2}$ ．

查看试题解析
17. 解不等式组 ${\begin{array}{l} x - 3 \geq 3 (x + 1) ① ， \\ \frac{1 + 2 x}{3} > x - 1 ② ， \end{array}$ 并将其解集表示在如图所示的数轴上．

查看试题解析
18. 解方程： $\frac{2 - x}{3 + x} = \frac{1}{4} + \frac{1}{x + 3}$ ．

查看试题解析
19. 已知：如图， $▱ A B C D$ 中，点 $E$ ， $F$ 是对角线 $B D$ 上的两点，顺次连接点A， $E$ ， $C$ ， $F$ ， A，得到四边形 $A E C F$ ．若四边形 $A E C F$ 也是平行四边形，求证： $B E = D F$ ．

查看试题解析
20. 2023年5月8日是第76个“世界红十字日”，今年的主题是“生命教育，‘救’在身边”．目前，太原市许多公共场所已配置急救设备自动体外除颤器（AED），用来抢救心脏骤停虫者某高校先后两次购置AED设备，第一次总费用为88000元，第二次总费用为120000元．已知第二次比第一次多购置了2台，但每台价格是第一次每台价格的 $\frac{10}{11}$ ．

(1)、该校第一次购置AED设备多少台？

(2)、该校计划将所购置的AED设备用壁挂式、立式两种存储柜分散固定在校园内，已知一共需购买两种存储柜10个，其售价分别如下图所示．若要使购买存储柜的总费用不超过7000元，最多可购买立式存储柜多少个？

查看试题解析
21. 如图，已知 $△ A B C$ 是等边三角形，点 $D$ 是 $A B$ 边上的一点．

(1)、求作：直线 $D E$ ，使 $D E ⊥ B C$ 于点 $E$ （要求：尺规作图，保留作图痕迹，不写作法）；

(2)、在（1）所作图中，取 $A C$ 边上的点 $F$ ，使 $A F = A D$ ，连接 $D F$ ， $E F$ ．若 $B D = 2 A D$ ，请按要求补全图形，并证明四边形 $D B E F$ 是平行四边形（若完成第（1）题有困难，可画草图完成第（2）题）．

查看试题解析

22. 阅读下列材料，完成相应的任务．

真分式与假分式

将两个整数相除（除数不为零）表示成分数，可能得到真分数，也可能得到假分数；类似地，分式也有真、假之分．我们规定，在分式中，当分子中整式的次数大于或等于分母中整式的次数，如 $\frac{x^{2} - 1}{x}$ ， $\frac{2 x^{2} + 1}{x^{2} - x}$ ，称为假分式；当分子中整式的次数小于分母中整式的次数时，如 $\frac{3}{x + 1}$ ， $\frac{x^{2} - 1}{x^{3} + 2 x - 3}$ ，称为真分式．

一些假分数可以化为带分数，即整数与真分数之和，如： $\frac{7}{3} = \frac{2 \times 3 + 1}{3} = 2 + \frac{1}{3} = 2 \frac{1}{3}$ ；类似地，我们也可以把一些假分式化为带分式，即整式与真分式之和（或差）的形式．例： $\frac{x^{2} - 1}{x} = \frac{x^{2}}{x} - \frac{1}{x} = x - \frac{1}{x}$ ； $\frac{2 x^{2} + 1}{x^{2} - x} = \frac{2 (x^{2} - x) + 2 x + 1}{x^{2} - x} = 2 + \frac{2 x + 1}{x^{2} - x}$ ．

任务：

(1)、下列分式中，是假分式（填序号）：

① $\frac{m^{2} + m}{2 m^{2} - 3}$ ；② $\frac{3}{x^{2}}$ ；③ $\frac{x^{3} - 3 x^{2} + 3}{5 x^{2} - 2 x}$ ；

(2)、小彬将一个假分式化成带分式的结果为

x + 1 + \frac{2 x + 1}{x - 1}

，请求出原来的假分式；

(3)、请从下面

A ， B

两题中任选一题作答．我选择． A.将假分式

\frac{2 x - 1}{x + 1}

化成带分式的结果为；B.将假分式

\frac{3 x^{2} - 1}{x - 1}

化成带分式的结果为 ▲ ．

查看试题解析

23. 综合与实践：

问题情境：数学课上，老师让每个组准备了一张如图1所示的等腰三角形纸片（即 $△ A B C$ ），其中 $A B = A C = 2 \sqrt{5}$ ， $B C = 4$ ， $A D$ 是 $B C$ 边上的中线．老师要求各个小组结合所学的图形变化的知识展开数学．
探究

(1)、初步分析： “勤学”小组发现图1中的 $A D$ 与 $B C$ 相等，请你证明这一结论；

(2)、操作探究： “善思”小组将 $△ A B C$ 纸片沿 $A D$ 剪开，然后保持 $△ A B D$ 不动，将 $△ A C D$ 从图1的位置开始运动．
①如图2，将 $△ A C D$ 绕点 $C$ 逆时针旋转 $90 °$ 得到 $△ F C E$ ，点 $E$ ， $F$ 分别是 $D$ ， $A$ 的对应点，连接 $B E$ .猜想线段 $A B$ 与 $B E$ 之间的数量关系与位置关系，并说明理由；
②如图3，将 $△ A C D$ 沿射线 $B C$ 方向平移得到 $△ G H P$ ，点 $G$ ， $H$ ， $P$ 分别是 $A$ ， $D$ ， $C$ 的对应点．连接 $A P$ ， $C G$ 交于点 $O$ ．
请从下面 $A ， B$ 两题中任选一题作答．我选择 ▲ 题．
A、当以 $A$ ， $C$ ， $O$ 为顶点的三角形是等腰三角形时，直接写出平移的距离．
B、当以 $A$ ， $C$ ， $O$ 为顶点的三角形是直角三角形时，直接写出平移的距离．

查看试题解析