山西省忻州市2022-2023学年八年级下学期7月期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列各式为二次根式的是( )A、 B、 C、 D、2. 某鞋店在做市场调查时,为了提高销售量,商家最应关注鞋子型号的( )A、众数 B、平均数 C、中位数 D、极差3. 下列各组数中,是勾股数的是( )A、3,4,4 B、5,6,7 C、 , , D、5,12,134. 若在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 在平行四边形中,已知 , 则( )A、 B、 C、 D、6. 已知正比例函数经过点 , 则( )A、 B、 C、 D、7. 一组数据为1,2,3,5,a,这组数据的平均数为3.5,则( )A、7 B、6.5 C、6 D、48. 如图,在四边形中, , , , , 且 , 则四边形的面积为( )
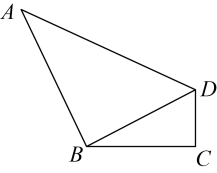 A、 B、 C、 D、9. 如图,在矩形中,过的中点O作交 , 于点E,F,连接 , , 若四边形的面积为 , , 则四边形的周长为( )
A、 B、 C、 D、9. 如图,在矩形中,过的中点O作交 , 于点E,F,连接 , , 若四边形的面积为 , , 则四边形的周长为( )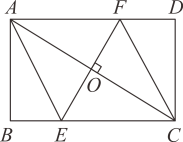 A、 B、 C、 D、10. 已知 , , 若一次函数与线段有交点,则k的取值范围为( )A、 B、 C、或 D、或
A、 B、 C、 D、10. 已知 , , 若一次函数与线段有交点,则k的取值范围为( )A、 B、 C、或 D、或二、填空题
-
11. 一组数据:11,13,14,8,6的中位数是 .12. 比较大小:13. 甲、乙两位同学的跳远成绩(单位:米)的平均数为 , , 方差为 , , 则甲、乙同学成绩较为稳定的是 . (填“甲”或“乙”)14. 直线过点 , 现将其向上平移2个单位长度,平移后的解析式为 .15. 如图,在矩形中,对角线 , 交于点O, , , 垂足为点E,若 , 则的长为 .
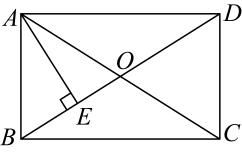
三、解答题
-
16.(1)、计算: .(2)、 .17. 某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手,两队每个队员的身高(单位:cm)如下:
甲队
177
179
178
179
177
178
178
179
178
177
平均数
中位数
众数
方差
甲队
178
a
178
c
乙队
177.1
177
b
0.89

两组样本数据的平均数,中位数,众数,方差如表中数据所示:
(1)、表中 , .(2)、请计算甲队的方差c,并判断哪队队员身高更整齐.18. 如图,在中,分别在边上,且 , 求证:四边形是平行四边形.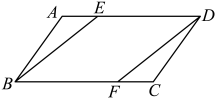 19. 某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:)和材积量(单位:),得到如下数据:
19. 某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:)和材积量(单位:),得到如下数据:样本号
1
2
3
4
5
6
7
8
9
10
根部横截面积x
0.04
0.06
0.04
0.08
0.08
0.05
0.05
0.07
0.07
0.06
材积量y
0.25
0.40
0.22
0.54
0.51
0.34
0.36
0.46
0.42
0.40
(1)、估计该林区一颗这种树木平均根部横截面积与平均材积量.(2)、现测量了该林区部分这种树木的根部横截面积,经过测算得到这种树木的根部横截面积总和为 . 已知树木的材积量与其根部横截面积近似成正比.利用以上数据估计该林区这种树木的总材积量.20. 今年暑假,学校计划组织八年级的同学参观大学城,经调查得八年级共有670名同学,计划租用12辆客车,现有甲、乙两种型号的客车,它们的载客量和租金如下表:租金/(元/辆)
载客量/(座/辆)
甲种客车
3500
50
乙种客车
4000
60
(1)、如果恰好一次性将670名学生送往大学城且客车全部坐满,那么应租用甲、乙两种客车各多少辆?(2)、设租用甲种客车x辆,租车费用y元.①求y与x的函数关系式.(要求写出x的取值范围)
②在保证所有同学均能送达大学城的情况下,怎样租车费用最低,最低费用是多少元?
21. 阅读与思考阅读下列材料并完成相应的任务.
我国是最早了解和应用勾股定理的国家之一,古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用,古希腊数学家毕达哥拉斯首先证明了勾股定理,在西方,勾股定理又称为“毕达哥拉斯定理”.关于勾股定理的研究还有一个很重要的内容是勾股数组,在课本中我们已经了解到“能够成为直角三角形三条边的三个正整数称为勾股数”.
以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数 , 则 , 和是勾股数.
方法2:若任取两个正整数m和 , 则 , , 是勾股数.
任务:
(1)、在以上两种方法中任选一种,证明以a,b,c为边长的是直角三角形.(2)、学校园林设计师按照如图所示的方式摆放兰花,已知这四个直角三角形全等,且直角三角形的三边是勾股数,较短的直角边长为 , 要求在每个直角三角形的三个顶点处需要摆放一盆兰花,每个直角三角形的三条边间隔1米摆放一盆兰花,请你计算出总共需要的兰花数量. 22. 综合与实践
22. 综合与实践【问题情境】在学校活动课上,樊老师让同学们探究特殊平行四边形的性质,小明和他的小伙伴们准备了如图1所示的正方形 , 连接对角线 , 在上取一点P,连接 , 延长至点E,连接 , 交于点F,且 .
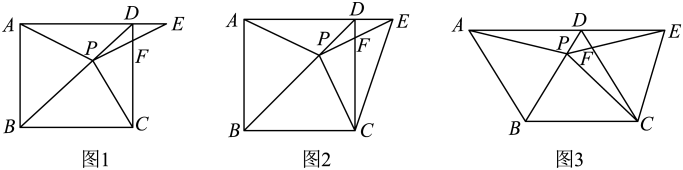 (1)、如图1,小明连接了 , 小伙伴们发现了与之间存在一定的关系,其数量关系为 , 位置关系为 .(2)、如图2,小明连接了 , 小伙伴们发现了和之间存在一定的数量关系,请你帮助小明和小伙伴们探究和之间的数量关系,并说明理由.(3)、如图3.小明将正方形改为菱形 , 当时,请直接写出与之间的数量关系.23. 综合与探究
(1)、如图1,小明连接了 , 小伙伴们发现了与之间存在一定的关系,其数量关系为 , 位置关系为 .(2)、如图2,小明连接了 , 小伙伴们发现了和之间存在一定的数量关系,请你帮助小明和小伙伴们探究和之间的数量关系,并说明理由.(3)、如图3.小明将正方形改为菱形 , 当时,请直接写出与之间的数量关系.23. 综合与探究如图,一次函数与轴交于点 , 与轴交于点 , 一次函数与轴交于点 , 与轴交于点 , 且它们的图像交于点 .
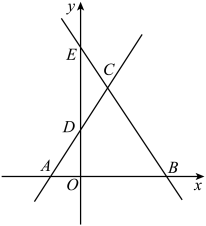 (1)、求点与点的坐标.(2)、当时,求自变量的取值范围(直接写出结果).(3)、在轴上是否存在一点 , 使得 , 如果存在,请求出点的坐标;如果不存在,请说明理由.
(1)、求点与点的坐标.(2)、当时,求自变量的取值范围(直接写出结果).(3)、在轴上是否存在一点 , 使得 , 如果存在,请求出点的坐标;如果不存在,请说明理由.