山西省吕梁市中阳县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列函数中,是的一次函数的是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 直角三角形的三边长分别为3,4,x,则的值可能为( )A、5 B、 C、7 D、5或4. 在平行四边形中, , 则的度数为( )A、 B、 C、 D、5. 八年级(1)班的期末综合成绩按照课堂表现、作业成绩、考试成绩2:3:5的比例计算,小明的课堂表现为80分,作业成绩为90分,考试成绩为85分,那么小明的期末综合成绩为( )A、85分 B、85.5分 C、86分 D、86.5分6. 如图,菱形中,分别是的中点,若菱形的周长为 , 则的长为( )
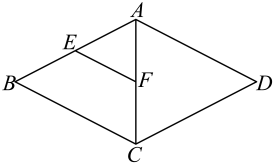 A、 B、 C、 D、7. 一次函数的图像如图所示,当时,的取值范围是( )
A、 B、 C、 D、7. 一次函数的图像如图所示,当时,的取值范围是( )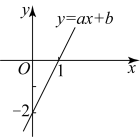 A、 B、 C、 D、8. 如图所示的是丽丽家正方形后院的示意图,丽丽家打算在正方形后院打造一个的正方形游泳池和一个的正方形花园,剩下阴影部分铺满瓷砖,则阴影部分的面积为( )
A、 B、 C、 D、8. 如图所示的是丽丽家正方形后院的示意图,丽丽家打算在正方形后院打造一个的正方形游泳池和一个的正方形花园,剩下阴影部分铺满瓷砖,则阴影部分的面积为( )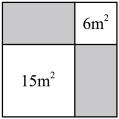 A、 B、 C、 D、9. 已知小明家、体育馆、图书馆依次在同一条直线上.小明从家出发,匀速骑行到达体育馆;在体育馆停留一段时间后,匀速步行到达图书馆;在图书馆停留一段时间后,匀速骑行返回家中.给出的图象反映了这个过程中小明离开家的距离与离开家的时间之间的对应关系.下列说法不正确是( )
A、 B、 C、 D、9. 已知小明家、体育馆、图书馆依次在同一条直线上.小明从家出发,匀速骑行到达体育馆;在体育馆停留一段时间后,匀速步行到达图书馆;在图书馆停留一段时间后,匀速骑行返回家中.给出的图象反映了这个过程中小明离开家的距离与离开家的时间之间的对应关系.下列说法不正确是( )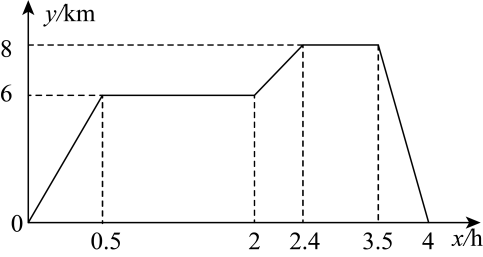 A、体育馆与图书馆之间的距离为 B、小明从体育馆到图书馆的步行速度为 C、小明在体育馆停留了分钟 D、小明从家去体育馆的速度比从图书馆回家的速度快10. 小明用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则图形的总长度与图形个数之间的关系式为( )
A、体育馆与图书馆之间的距离为 B、小明从体育馆到图书馆的步行速度为 C、小明在体育馆停留了分钟 D、小明从家去体育馆的速度比从图书馆回家的速度快10. 小明用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则图形的总长度与图形个数之间的关系式为( )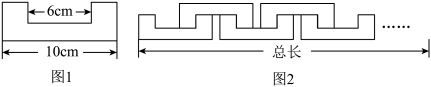 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
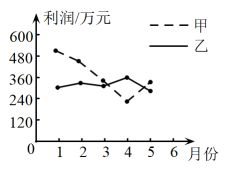
11. 若在实数范围内有意义,则实数的取值范围是 .12. 如图所示的是甲、乙两公司上半年前5个月利润的折线统计图,则(填“>”或“<”).
 13. 将直线向右平移3个单位长度后与轴相交于点 , 则点的坐标为 .14. 攀岩是一项在天然岩壁或人工岩壁上进行的向上攀爬的运动项目.如图,攀岩墙近似一个长方体的两个侧面,小天根据学过的数学知识准确地判断出从点攀爬到点的最短路径为米.
13. 将直线向右平移3个单位长度后与轴相交于点 , 则点的坐标为 .14. 攀岩是一项在天然岩壁或人工岩壁上进行的向上攀爬的运动项目.如图,攀岩墙近似一个长方体的两个侧面,小天根据学过的数学知识准确地判断出从点攀爬到点的最短路径为米.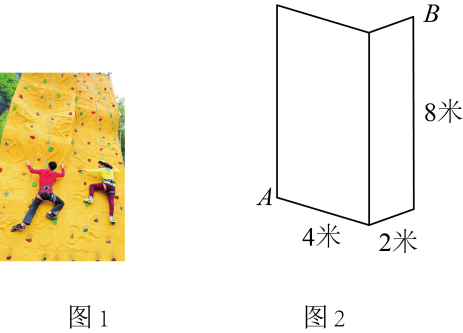 15. 在平面直角坐标系中,一次函数的图像分别交轴,轴于B,C两点,点A坐标为 , 直线上有一点 , 使得是以点A为直角顶点的等腰直角三角形,则 .
15. 在平面直角坐标系中,一次函数的图像分别交轴,轴于B,C两点,点A坐标为 , 直线上有一点 , 使得是以点A为直角顶点的等腰直角三角形,则 .三、解答题
-
16.(1)、计算: .(2)、下面是小华同学解答题目的过程,请认真阅读并完成相应任务.
计算: .
解:原式第一步
第二步
第三步
任务一:以上步骤中,从第 ▲ 步开始出现错误,这一步错误的原因是 ▲ .
任务二:请写出正确的计算过程.
17. 如图,是菱形对角线的交点,过点作 , 过点作 . 与相交于点 . 求证:四边形是矩形. 18. 为了解学生对五一劳动节上映的《长空之王》与《灌篮高手》两部电影的评价,某调查小组从该校八年级中随机抽取了20名学生对这两部作品分别进行打分(满分10分),并进行整理、描述和分析,下面给出了部分信息.
18. 为了解学生对五一劳动节上映的《长空之王》与《灌篮高手》两部电影的评价,某调查小组从该校八年级中随机抽取了20名学生对这两部作品分别进行打分(满分10分),并进行整理、描述和分析,下面给出了部分信息.《长空之王》得分情况:7,8,7,10,7,6,9,9,10,10,8,9,8,6,6,10,9,7,9,9.
《灌篮高手》的得分统计图:
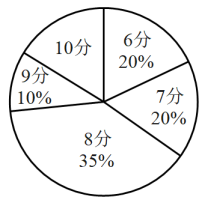
抽取的学生对两部作品分别打分的平均数,众数和中位数:
平均数
众数
中位数
《长空之王》
8.2
8.5
《灌篮高手》
7.8
8
根据以上信息,解答下列问题:
(1)、上述图表中的 , .(2)、根据上述数据,你认为该校八年级学生对哪部作品评价更高?请说明理由(写出一条理由即可).19. 已知一次函数的图象与轴相交于点 , 与轴正半轴相交于点 , 且 .(1)、求该一次函数的解析式.(2)、若点和点在该一次函数的图象上,求的值.20. 甲、乙两根蜡烛燃烧时剩余部分的高度与燃烧时间之间的关系如图所示,已知 , 请根据所提供的信息解答下列问题: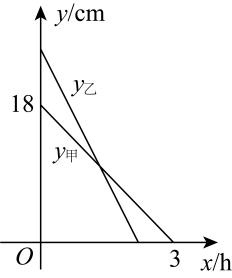 (1)、乙蜡烛燃烧前的高度是 , 乙从点燃到燃尽所用的时间是 .(2)、燃烧多长时间时,甲、乙两根蜡烛的高度一样长?21. 阅读与思考
(1)、乙蜡烛燃烧前的高度是 , 乙从点燃到燃尽所用的时间是 .(2)、燃烧多长时间时,甲、乙两根蜡烛的高度一样长?21. 阅读与思考请你阅读下列材料,并完成相应的任务.
裂项法,是数学中求和的一种方法,是分解与组合思想在求和中的具体应用.具体方法是将求和中的每一项进行分解,然后重新组合,使之能消去一些项,最终达到求和的目的.我们以往的学习中已经接触过分数裂项求和.例如: .
在学习完二次根式后我们又掌握了一种根式裂项.例如: , .
(1)、模仿材料中的计算方法,化简: .(2)、观察上面的计算过程,直接写出式子 .(3)、利用根式裂项求解: .22. 综合与实践问题情境:在数学活动课上,数学老师让同学们用一张矩形纸片进行探究活动.
小亮准备了矩形纸片 , 其中是的中点,将沿折叠,点的对应点为 .
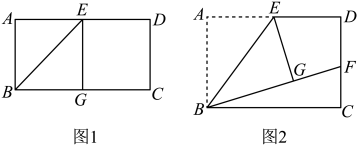 (1)、观察发现:如图1,当点恰好在边上时,小亮发现与存在一定的数量关系,其数量关系是 .(2)、探索猜想:如图2,当点在矩形内部时,延长交边于点 . 试猜想线段与之间的数量关系,并说明理由.(3)、拓展延伸:当点在矩形内部时,若 , 直接写出线段与的数量关系.23. 综合与探究
(1)、观察发现:如图1,当点恰好在边上时,小亮发现与存在一定的数量关系,其数量关系是 .(2)、探索猜想:如图2,当点在矩形内部时,延长交边于点 . 试猜想线段与之间的数量关系,并说明理由.(3)、拓展延伸:当点在矩形内部时,若 , 直接写出线段与的数量关系.23. 综合与探究如图,直线分别交轴,轴于点 , 过点A作直线分别交轴,轴于点 , .
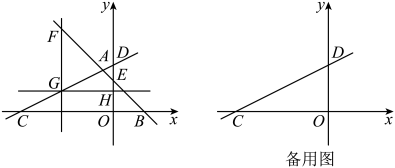 (1)、求直线的解析式.(2)、在轴左侧作直线轴,分别交直线 , 于点 . 当时,过点作直线轴,交轴于点 . 能否在直线上找一点 , 使的值最小,求出点的坐标.(3)、为直线上一点,在(2)的条件下,轴上是否存在点使得以为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求直线的解析式.(2)、在轴左侧作直线轴,分别交直线 , 于点 . 当时,过点作直线轴,交轴于点 . 能否在直线上找一点 , 使的值最小,求出点的坐标.(3)、为直线上一点,在(2)的条件下,轴上是否存在点使得以为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.