山西省吕梁市孝义市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 二次根式在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 下列图象中不能表示是的函数的是( )A、
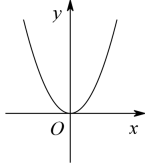 B、
B、 C、
C、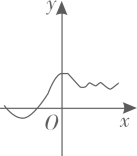 D、
D、 3. 农历五月初五是端午节,为继承和发扬民族优秀传统文化,某班组织“粽享文化”为主题的演讲比赛,比赛成绩由高到低设立一等奖1名,二等奖3名,三等奖5名,甲同学参加了演讲比赛,并且比赛成绩进入了前19名(比赛成绩都不相同),该同学想知道自己能否获奖,需比较自己的成绩与前19名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差4. 某农科所在某次实验中,对甲、乙两种水稻进行产量稳定实验,各选取了5块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1000千克/亩,方差 . 为保证产量稳定,适合推广的品种为( )A、甲 B、乙 C、甲、乙均可 D、无法确定5. 如图,毕达哥拉斯用图1,图2证明了.个重要的数学定理,他的思路是图1中拼成的正方形与图2中拼成的正方形面积相等,通过面积相等可以得到: , 整理得 . 证明的这个定理是( )
3. 农历五月初五是端午节,为继承和发扬民族优秀传统文化,某班组织“粽享文化”为主题的演讲比赛,比赛成绩由高到低设立一等奖1名,二等奖3名,三等奖5名,甲同学参加了演讲比赛,并且比赛成绩进入了前19名(比赛成绩都不相同),该同学想知道自己能否获奖,需比较自己的成绩与前19名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差4. 某农科所在某次实验中,对甲、乙两种水稻进行产量稳定实验,各选取了5块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1000千克/亩,方差 . 为保证产量稳定,适合推广的品种为( )A、甲 B、乙 C、甲、乙均可 D、无法确定5. 如图,毕达哥拉斯用图1,图2证明了.个重要的数学定理,他的思路是图1中拼成的正方形与图2中拼成的正方形面积相等,通过面积相等可以得到: , 整理得 . 证明的这个定理是( )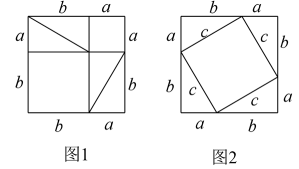 A、勾股定理 B、勾股定理的逆定理 C、祖晅定理 D、费马定理6. 数学课上,老师提出如下问题:如图,四边形是平行四边形,请同学们添加个条件使是矩形.小彤添加的条件是: . 则小彤判定是矩形的依据是( )
A、勾股定理 B、勾股定理的逆定理 C、祖晅定理 D、费马定理6. 数学课上,老师提出如下问题:如图,四边形是平行四边形,请同学们添加个条件使是矩形.小彤添加的条件是: . 则小彤判定是矩形的依据是( )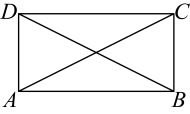 A、矩形的四个角都是直角 B、矩形的对角线相等 C、有三个角是直角的四边形是矩形 D、对角线相等的平行四边形是矩形7. 如图,在中, , , , 点是的中点,连接 , 则的长为( )
A、矩形的四个角都是直角 B、矩形的对角线相等 C、有三个角是直角的四边形是矩形 D、对角线相等的平行四边形是矩形7. 如图,在中, , , , 点是的中点,连接 , 则的长为( ) A、 B、 C、3 D、48. 如图,正方形木板的面积是 , 在这个木板上截出面积为的正方形 , 连接 , 则的长度为( )
A、 B、 C、3 D、48. 如图,正方形木板的面积是 , 在这个木板上截出面积为的正方形 , 连接 , 则的长度为( )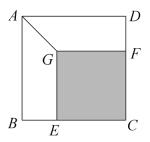 A、 B、 C、 D、9. 如图, , 以点为圆心,为半径画弧交 , 于点 , ;分别以点 , 为圆心大于为半径画弧,两弧交于点;以点为顶点作 , 射线与交于点 , 连接;则四边形的面积为( )
A、 B、 C、 D、9. 如图, , 以点为圆心,为半径画弧交 , 于点 , ;分别以点 , 为圆心大于为半径画弧,两弧交于点;以点为顶点作 , 射线与交于点 , 连接;则四边形的面积为( ) A、 B、 C、 D、10. 同一平面直角坐标系中,一次函数与( , 为常数, , )的图像可能是( )A、
A、 B、 C、 D、10. 同一平面直角坐标系中,一次函数与( , 为常数, , )的图像可能是( )A、 B、
B、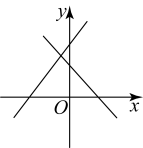 C、
C、 D、
D、
二、填空题
-
11. 计算的结果是12. 学校为了促进学生积极参加体育运动,决定给篮球队24名运动员购买运动鞋,下表是24名运动员鞋码统计表,根据统计表信息,这24名运动员鞋码的众数是 .
鞋码
25
26
人数
1
4
8
7
4
13. 某水果店以2.5元的价格批发了苹果,以4元的价格销售,销售这苹果的总利润为(元),则与的函数关系式为14. 如图,将矩形纸片沿折叠,使点落在处,交于点 , 若 , , 则的长为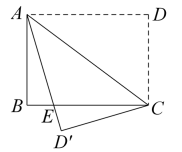 15. 如图,正方形的对角线 , 交于点 , 点是上一点,交于点 , 若 , , 则的长为
15. 如图,正方形的对角线 , 交于点 , 点是上一点,交于点 , 若 , , 则的长为
三、解答题
-
16. 计算(1)、(2)、17. 如图,在边长均为1的小正方形网格中,线段的端点都在格点上.(小正方形的顶点叫格点.)
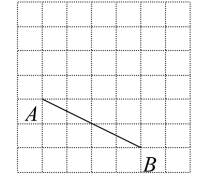 (1)、实践与操作:
(1)、实践与操作:以为一边作矩形 , 使;(点 , 画在格点上)
(2)、推理与计算:线段的长为 , 矩形的面积为 .
18. 2023年6月5日是第50个世界环境日,今年的主题是“减塑捡塑”,旨在提高人们对塑料污染的认识,鼓励人们减少使用一次性塑料制品.为了庆祝第50个世界环境日,学校举办环境保护知识竞赛活动,竞赛内容分“自然环境保护”,“地球生物保护”,“人类环境保护”,“生态环境保护”四个项日,下表是小亮和小彬的各项成绩:(百分制)项目
自然环境保护
地球生物保护
人类环境保护
生态环境保护
小亮
95
90
85
90
小彬
80
90
100
90
若“自然环境保护”,“地球生物保护”,“人类环境保护”,“生态环境保护”四个项目按确定综合成绩,则小亮和小彬谁的综合成绩高?请通过计算说明理由.
19. 塔吊是建筑工地上最常用的一种起重设备,又名“塔式起重机”,用来吊施工用的钢筋、木楞、混凝土、钢管等施工的原材料.如图1是塔吊实物图,图2是塔吊示意图,线段 , 表示钢丝绳,表示起重臂, , 综合与实践小组向工人了解到如下信息:米,米,米.求钢丝绳的长度(参考数值:)
 20. 下面是小宇同学写的一篇数学日记,请你认真阅读并完成相应学习任务.
20. 下面是小宇同学写的一篇数学日记,请你认真阅读并完成相应学习任务.用一次函数的观点认识方程(组)、不等式
任何一个以为未知数的一元一次方程都可以变形为的形式,所以一元一次方程的解,相当于某个一次函数的图象与轴交点的横坐标.如图 , 一次函数的图象与轴交点的横坐标为 , 则方程的解为
任何一个以为未知数的一元一次不等式都可以变形为或的形式,所以解一元一次不等式,相当于求某个一次函数的函数值大于或小于时,自变量的取值范围.如图 , 根据图象可知,一次函数 , 当时,的取值范围是 , 所以不等式的解集为 ▲ ▲ ;
任何一个含未知数和的二元一次方程,都可以改写成( , 是常数,)的形式.含未知数和的两个二元一次方程组成的二元一次方程组,都对应两个一次函数,从“数”的角度看,解这样的方程组相当于求自变量为何值时两个函数值相等,以及这个函数值是多少;从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标.如图 , 直线与直线的交点的坐标为 , 则二元一次方程组的解为 ▲ ▲ .

任务:
(1)、上述材料“”处不等式“”的解集为 , “”处二元一次方程组的解为;(2)、上述材料中主要运用的数学思想是____;A、数形结合思想 B、统计思想 C、方程思想(3)、①如图4,直线与直线的交点坐标火 , 则关于 , 的二元一次方程组的解为;②如图 , 一次函数的图象与轴的交点坐标为 , 与轴的交点坐标为 , 则不等式的解集为 .
 21. 综合与实践
21. 综合与实践如图1,在正方形中,点 , 分别是边 , 上的点,且 .
 (1)、求证: .(2)、如图2,在图1的基础上,过点作的垂线,与正方形的外角的平分线交于点 , 连接 . 求证:四边形是平行四边形.(提示:在上截取 , 连接)(3)、如图3,连接 , 若四边形的面积是9, , 则直接写出的长.22. 综合与探究
(1)、求证: .(2)、如图2,在图1的基础上,过点作的垂线,与正方形的外角的平分线交于点 , 连接 . 求证:四边形是平行四边形.(提示:在上截取 , 连接)(3)、如图3,连接 , 若四边形的面积是9, , 则直接写出的长.22. 综合与探究如图1,一次函数的图象与坐标轴交于 , 两点,点的坐标为 , 点是线段上一动点,点的横坐标为 .
 (1)、直接写出点A,B的坐标及直线的解析式;(2)、如图1,连接 , 当的面积等于的面积时,求点的坐标;(3)、如图2,过点作直线的平行线 , 在直线上是否存在一点 , 使四边形是菱形?若存在,请直接写出点的坐标;若不存在,说明理由.
(1)、直接写出点A,B的坐标及直线的解析式;(2)、如图1,连接 , 当的面积等于的面积时,求点的坐标;(3)、如图2,过点作直线的平行线 , 在直线上是否存在一点 , 使四边形是菱形?若存在,请直接写出点的坐标;若不存在,说明理由.