山西省临汾地区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 限高标志牌是指禁止装载高度超过标志所示数值的车辆通行.如图所示是某桥洞的限高标志牌,则下列装载高度的车辆能通过此桥洞的是( )
 A、4.5 B、5.5 C、6 D、6.52. 剪纸又称刻纸,是一种镂空艺术,在视觉上给人以透空的感觉和艺术的享受.下列四个剪纸作品中,是中心对称图形的是( )A、
A、4.5 B、5.5 C、6 D、6.52. 剪纸又称刻纸,是一种镂空艺术,在视觉上给人以透空的感觉和艺术的享受.下列四个剪纸作品中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列各式从左边到右边的变形,属于因式分解的是( )A、 B、 C、 D、4. 请阅读以下关于解答“在中, , 求证:”的过程:
3. 下列各式从左边到右边的变形,属于因式分解的是( )A、 B、 C、 D、4. 请阅读以下关于解答“在中, , 求证:”的过程:证明:假设 .
这与“三角形三个内角的和等于”相矛盾.
假设不成立.
.
这种证明方法是( )
A、综合法 B、反证法 C、枚举法 D、归纳法5. 一个不等式组 , 那么它的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 依据所标数据,下列图形中一定为平行四边形的是( )A、
6. 依据所标数据,下列图形中一定为平行四边形的是( )A、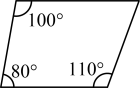 B、
B、 C、
C、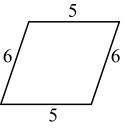 D、
D、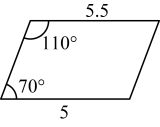 7. 化简的结果是( )A、 B、 C、 D、8. 如图,在正五边形中,为边延长线上一点,连接 , 则的度数为( )
7. 化简的结果是( )A、 B、 C、 D、8. 如图,在正五边形中,为边延长线上一点,连接 , 则的度数为( ) A、 B、 C、 D、9. 6月进入了毕业季,某校九年级班主任准备给自己的学生买一些相册,并把初中三年来学生的照片放进去,这些照片记录了他们初中三年的点点滴滴.目前有A,B两款相册比较合适,其中A款相册的单价比B款相册的单价贵3元,用1000元购买A款相册的数量是用425元购买B款相册数量的2倍,求B款相册的单价.若设B款相册的单价为x元,则根据题意可列方程为( )A、 B、 C、 D、10. 如图,在中,是边上一点,是边的中点,平分 . 若 , 则的长为( )
A、 B、 C、 D、9. 6月进入了毕业季,某校九年级班主任准备给自己的学生买一些相册,并把初中三年来学生的照片放进去,这些照片记录了他们初中三年的点点滴滴.目前有A,B两款相册比较合适,其中A款相册的单价比B款相册的单价贵3元,用1000元购买A款相册的数量是用425元购买B款相册数量的2倍,求B款相册的单价.若设B款相册的单价为x元,则根据题意可列方程为( )A、 B、 C、 D、10. 如图,在中,是边上一点,是边的中点,平分 . 若 , 则的长为( ) A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题
-
11. 若分式的值为0,则的值为 .12. 永祚寺双塔(如图1),又名凌霄双塔,是山西省太原市现存的最高的古建筑,十三层均为正八边形楼阁式空心砖塔.如图2所示的正八边形是双塔其中一层的平面示意图,则其外角和的度数为 .
 13. 某品牌乳胶枕的进价为200元,商店以300元的价格出售.店庆期间,商店为让利于顾客,计划以利润率不低于的价格降价出售,则该乳胶枕最多可降价元.14. 如图,平分是上一点,过点分别作于点交于点 . 若 , 则的长为 .
13. 某品牌乳胶枕的进价为200元,商店以300元的价格出售.店庆期间,商店为让利于顾客,计划以利润率不低于的价格降价出售,则该乳胶枕最多可降价元.14. 如图,平分是上一点,过点分别作于点交于点 . 若 , 则的长为 . 15. 如图,在中, , 将绕点按逆时针方向旋转得到 , 连接 , 延长交于点 . 若 , 则的长为 .
15. 如图,在中, , 将绕点按逆时针方向旋转得到 , 连接 , 延长交于点 . 若 , 则的长为 .
三、解答题
-
16.(1)、因式分解:;(2)、下面是小明同学对多项式进行因式分解的过程,请仔细阅读并完成相应的任务.
解:原式……第一步
……第二步
……第三步
……第四步
任务:
①在上述过程中,第一步依据的数学公式用字母表示为;
②第四步因式分解的方法是提公因式法,其依据的运算律为;
③第步出现错误,错误的原因是;
④因式分解正确的结果为 .
17. 先化简,再求值: , 其中 .18. 已知:如图,在ABCD中,点E、F分别在AD、BC上,且∠ABE=∠CDF.求证:四边形BFDE是平行四边形.
 19. 如图,在平面直角坐标系中,三个顶点的坐标分别为 , .
19. 如图,在平面直角坐标系中,三个顶点的坐标分别为 , . (1)、将绕点旋转 , 请画出旋转后对应的 .(2)、将平移,使点的对应点的坐标为 , 点的对应点为 , 点的对应点为 , 请画出平移后对应的 .(3)、与关于点成中心对称.20. 为弘扬爱国精神,传承中华优秀传统文化,某校组织了以“诗词里的中国”为主题的比赛,设置A,B两种奖品.校学生会计划去某超市购买A,B两种奖品共300个,A种奖品每个20元,B种奖品每个15元,该超市对同时购买这两种奖品的顾客有两种销售方案(只能选择其中一种).
(1)、将绕点旋转 , 请画出旋转后对应的 .(2)、将平移,使点的对应点的坐标为 , 点的对应点为 , 点的对应点为 , 请画出平移后对应的 .(3)、与关于点成中心对称.20. 为弘扬爱国精神,传承中华优秀传统文化,某校组织了以“诗词里的中国”为主题的比赛,设置A,B两种奖品.校学生会计划去某超市购买A,B两种奖品共300个,A种奖品每个20元,B种奖品每个15元,该超市对同时购买这两种奖品的顾客有两种销售方案(只能选择其中一种).方案一:两种奖品都按原价购买,但每购买5个A种奖品赠送1个B种奖品.
方案二:A种奖品按原价购买,B种奖品每个打八折.
设校学生会计划购买个A种奖品,且是5的倍数,选择方案一的总费用为元,选择方案二的总费用为元.
(1)、请分别写出与之间的函数关系式.(2)、校学生会选择哪种方案支付的费用较少?21. 某班级组织同学们乘坐大巴车前往距学校的山西博物院开展“研学之旅”,大巴车从学校出发时,其中一位老师因有事耽误,没有赶上大巴车,因此比大巴车晚从学校自驾小汽车出发,并以大巴车倍的速度走同样的路线赶往山西博物院,结果与大巴车同时到达.求大巴车和小汽车的平均速度.22. 阅读与思考请阅读下列材料,并完成相应的任务.
年月日星期一
今天,同学们学习了三角形中位线定理的相关内容,知道了“三角形的中位线平行于第三边,且等于第三边的一半”.课下,对三角形中位线定理的相关知识进行了复习,并对它相关的命题产生了兴趣.如图1,在中,分别是边上的点,同学们提出了以下三个命题:
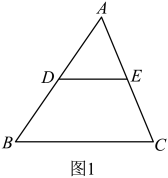
I.若是边的中点,且 , 则是边的中点.
II.若 , 且 , 则分别是边的中点.
III.若是边的中点,且 , 则是边的中点.
任务:
(1)、从所提出的三个命题中选择一个假命题,并在图2中画出反例.(要求:尺规作图,保留作图痕迹) (2)、从所提出的三个命题中选择一个真命题进行证明.23. 综合与实践
(2)、从所提出的三个命题中选择一个真命题进行证明.23. 综合与实践特例感知:
如图1,在等边三角形中,是延长线上一点,且 , 以为边作等边三角形 , 连接 , 分别过点作 , 过点作 , 交于点 , 连接与交于点 .


 (1)、试判断和的数量关系,并说明理由.(2)、猜想论证:将绕点按顺时针方向旋转一定角度得到图2,则(1)中和的数量关系是否仍然成立?请说明理由.(3)、拓展延伸:将如图1所示的绕点按逆时针方向旋转角度 , 当时,请直接写出的值.
(1)、试判断和的数量关系,并说明理由.(2)、猜想论证:将绕点按顺时针方向旋转一定角度得到图2,则(1)中和的数量关系是否仍然成立?请说明理由.(3)、拓展延伸:将如图1所示的绕点按逆时针方向旋转角度 , 当时,请直接写出的值.