山西省吕梁市交口县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{a - 4}$ 在实数范围内有意义，则 $a$ 的取值范围是（）

A、 $a \geq 4$ B、 $a \leq 4$ C、 $a \leq - 4$ D、 $a \geq - 4$

查看试题解析
2. 点 $(m ， 5)$ 在函数 $y = 2 x + 1$ 的图象上，则 $m$ 的值是（）

A、 $- 1$ B、 $1$ C、 $- 2$ D、 $2$

查看试题解析
3. 某专卖店专营某品牌女鞋，店主对上一周中不同尺码的鞋子销售情况统计如表：

尺码

35

36

37

38

39

平均每天销售数量（双）

2

8

10

6

2

该店主决定本周进货时，增加一些37码的女鞋，影响该店主决策的统计量是（　　）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
4. 如图，在等边△ABC中，D、E分别是边AB、BC的中点，DE＝2，则△ABC的周长为（）

A、9 B、12 C、16 D、18

查看试题解析
5. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，若 $∠ B A C = 55 °$ ，则 $∠ A O B$ 的度数是（）

A、 $55 °$ B、 $50 °$ C、 $70 °$ D、 $80 °$

查看试题解析
6. 我国是最早了解勾股定理的国家之一．早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于下列哪部著名数学著作中（）

A、《周髀算经》 B、《九章算术》 C、《海岛算经》 D、《几何原本》

查看试题解析
7. 一次函数 $y = k x + b$ 的图象如图所示，则下列结论正确的是（）

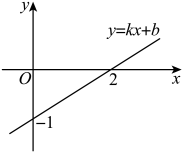A、 $k < 0$ B、 $b = - 1$ C、 $y$ 随 $x$ 的增大而减小 D、直线 $y = k x + b$ 与两坐标轴围成的图形面积为2

查看试题解析
8. 小明调查了班里 $40$ 名同学本学期购买课外书的本数，并将结果绘制成了如图所示的扇形统计图．则下列说法正确的是（）

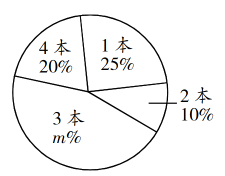A、 $m$ 的值为 $55$ B、众数为 $4$ C、平均数为 $3$ D、中位数为 $3$

查看试题解析
9. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{4} x + 3$ 交x轴于点A，交y轴于点B，以点A为圆心， $A B$ 长为半径画弧，交x轴的负半轴于点C，则直线 $B C$ 的解析式为（）

A、 $y = 3 x + 3$ B、 $y = 4 x + 3$ C、 $y = 4 x + 4$ D、 $y = - 4 x + 4$

查看试题解析
10. 如图所示的网格是正方形网格，点A，B，P是网格线的交点，则∠PAB+∠PBA=（）

A、30° B、45° C、60° D、75°

查看试题解析

二、填空题

11. 若一个长方形的长为 $2 \sqrt{6} c m$ ，宽为 $2 \sqrt{3} c m$ ，则它的面积为 $c m^{2}$ ．

查看试题解析
12. 命题“菱形的四条边都相等”的逆命题是.

查看试题解析

13. 2022年世界杯的成功举办，引起学生对足球的极大兴趣．某校开展了足球知识比赛，经过几轮笑选，八年级（1）班甲、乙、丙、丁四名同学的平均成绩（单位：分）及方差如下表：

	甲	乙	丙	丁
平均成绩/分	$96$	$98$	$98$	$96$
方差	$0.34$	$0.34$	$0.56$	$0.39$

如果要选出一名成绩较好且发挥稳定的同学代表班级参加比赛，那么应选择同学．

查看试题解析

14. 如图，已知函数 $y_{1} = a x + b$ 和 $y_{2} = k x$ 的图象相交于点 $P (- 4 ， - 2)$ ，则不等式 $a x + b < k x$ 的解集是．

查看试题解析
15. 如图，一张直角三角形纸片 $A B C$ ，两直角边 $A C = 4$ ， $B C = 8$ ，将 $△ A B C$ 沿直线折叠，使点 $B$ 与点 $A$ 重合，折痕为 $D E$ ，则 $D E$ 的长为．

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{32} + \sqrt{2} (\sqrt{2} - 3)$ ；

(2)、 $(\sqrt{3} - 2)^{2} + \sqrt{12} + 6 \sqrt{\frac{1}{3}}$ ．

查看试题解析
17. 端午节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售．经了解，甲种水果和乙种水果的进价与售价如下表所示：若超市购进这两种水果共 $200$ 千克，其中甲种水果的重量不低于乙种水果重量的 $3$ 倍，则超市应如何进货才能获得最大利润，最大利润是多少？
水果单价
甲
乙
进价（元/千克）
          $16$
          $20$
售价（元/千克）
          $20$
          $25$

查看试题解析

18. 现如今，环保这一理念越来越融入到我们的生活中．为了加强学生的环保意识，某中学举办我是环保小达人的演讲比赛，比赛分为入围赛和决赛两个赛段．全校学生积极响应，全部报名参加入围赛，随机抽取了若干名学生，调查他们每天课后练习演讲的时间，现将调查结果绘制成如下尚不完整的统计图表．请根据统计图表提供的信息，回答下列问题：

组别	练习时间（分钟）	频数（人）	百分比
$A$	$0 \leq x \leq 30$	$50$
$B$	$30 < x \leq 60$		$40 %$
$C$	$60 < x \leq 90$	$40$	$20 %$
$D$	$x > 90$

(1)、将下面的统计表和条形统计图补充完整；

(2)、若该校学生有

3000

人，请你估计每天课后练习时间超过

60

分钟的学生有多少人？

(3)、演讲决赛时，总成绩由内容、表达、风度、印象四部分组成，并按

3 ： 4 ： 2 ： 1

计算．进入冠亚军争夺的张明和赵亮的各项得分如下表：

	内容	表达	风度	印象
张明	$85$ 分	$78$ 分	$80$ 分	$90$ 分
赵亮	$75$ 分	$82$ 分	$85$ 分	$92$ 分

总成绩高的人为冠军，请你通过计算判断他俩谁获得冠军？

查看试题解析

19. 如图， $△ A B C$ 中， $∠ A B C = 90 °$ ，过点B作 $A C$ 的平行线，与 $∠ B A C$ 的平分线交于点D，点E是 $A C$ 上一点， $B E ⊥ A D$ 于点F，连接 $D E$ ．

(1)、求证：四边形 $A B D E$ 是菱形；

(2)、若 $A B = 2$ ， $∠ A D C = 90 °$ ，求 $B C$ 的长．

查看试题解析
20. 为落实“双减”政策，丰富课后服务的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个商店的优惠活动如下：
甲：所有商品按原价8.5折出售；
乙：一次购买商品总额不超过300元的按原价付费，超过300元的部分打7折．
设需要购买体育用品的原价总额为 $x$ 元，去甲商店购买实付 $y_{甲}$ 元，去乙商店购买实付 $y_{乙}$ 元，其函数图象如图所示.

(1)、分别求 $y_{甲}$ ， $y_{乙}$ 关于 $x$ 的函数关系式；

(2)、两图象交于点 $A$ ，求点 $A$ 坐标；

(3)、请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．

查看试题解析
21. 请阅读下列材料，并完成相应的任务．
勾股定理的证明
2000多年来，人们对勾股定理的证明颇感兴趣，不但因为这个定理重要，还因为这个定理贴近人们的生活实际，以致于古往今来，下至平民百姓，上至帝王总统，都愿意探讨研究它的证明，新的证法不断出现．其中，美国第20任总统詹姆斯·加菲尔德的证法在数学史上被传为佳话，他将两个完全相同的直角三角形拼成一个梯形，巧妙地用面积法给出了勾股定理的证明过程：
如图：
利用整体法，梯形的面积为 $S = \frac{1}{2} (a + b) (a + b) = a b + \frac{1}{2} (a^{2} + b^{2})$
利用分割法，梯形的面积为 $S = \frac{1}{2} a b + \frac{1}{2} c \cdot c + \frac{1}{2} a b = a b + \frac{1}{2} c^{2}$
……

(1)、按照上面的证明思路，完成该定理证明的剩余部分．

(2)、如图，在 $△ A B C$ 中， $∠ A = 60 °$ ， $∠ A C B = 75 °$ ， $C D ⊥ A B$ 于 $D$ ， $A C = 4$ ，求 $B C$ 的长．

查看试题解析
22. 综合与实践
问题情境：

数学活动课上，老师引导学生用一块等腰直角三角板和一个正方形展开探究活动．将正方形的一个顶点与等腰直角三角板的斜边的中点重合，观察不同的摆放方法下其中某些线段之间的数量关系与位置关系．

(1)、知识初探：
将等腰直角三角形 $A B C$ 与正方形 $O D E F$ 如图 $1$ 摆放，使正方形 $O D E F$ 的顶点 $O$ 与等腰直角三角板斜边 $A B$ 的中点 $O$ 重合，且 $O D$ 边经过点 $C$ ，请你直接写出 $D C$ 与 $B F$ 的数量关系和位置关系．

(2)、类比再探：
如图 $2$ ，正方形 $O D E F$ 的顶点 $O$ 与等腰直角三角板斜边 $A B$ 的中点 $O$ 重合， $O D$ 边不经过点 $C$ ，连接 $C D$ ， $B F$ ，此时 $D C$ 与 $B F$ 又有怎样的数量关系和位置关系？请说明理由．

(3)、拓展延伸：
如图 $3$ ，正方形 $O D E F$ 的顶点 $O$ 与等腰直角三角板斜边 $A B$ 的中点 $O$ 重合，正方形 $O D E F$ 的两条对角线交于点 $G$ ，连接 $C D$ ， $B D$ ，取 $B D$ 的中点 $H$ ，连接 $G H$ ，请你直接写出 $G H$ 与 $C D$ 之间的数量关系与位置关系．

查看试题解析
23. 综合与探究
如图，在平面直角坐标系中，直线 $l_{1} ： y = 2 x - 1$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ ， $B$ ，直线 $l_{2} ： y = k x + b$ 与 $x$ 轴， $y$ 轴分别交于点 $P$ ， $C (0 ， 1)$ ，两条直线交于点 $D$ ，且点 $D$ 的横坐标为 $\frac{4}{5}$ ；连接 $A C$ ．

(1)、求直线 $l_{2}$ 的函数解析式；

(2)、求 $△ A C D$ 的面积；

(3)、若点 $E$ 在直线 $l_{1}$ 上， $F$ 为坐标平面内任意一点，试探究：是否存在以点 $B$ ， $C$ ， $E$ ， $F$ 为顶点的四边形是矩形？若存在，请直接写出点 $F$ 的坐标；若不存在，请说明理由．

查看试题解析

水果单价	甲	乙
进价（元/千克）	$16$	$20$
售价（元/千克）	$20$	$25$

尺码	35	36	37	38	39
平均每天销售数量（双）	2	8	10	6	2