山西省大同市2022-2023学年八年级下学期7月期末数学试题

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 以下列长度的三条线段为边，不能组成直角三角形的是（）

A、3，4，5 B、5，6，7 C、5，12，13 D、7，24，25

查看试题解析
2. 下面计算正确的是（）

A、 $\sqrt{(- 2)^{2}} = - 2$ B、 $\sqrt{27} \div \sqrt{3} = 3$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $3 + \sqrt{3} = 3 \sqrt{3}$

查看试题解析
3. 一次函数y=﹣3x+2的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知点 $A (- 2 ， m)$ ， $B (3 ， n)$ 都在一次函数 $y = 2 x - 1$ 的图像上，则（）

A、 $m > n$ B、 $m = n$ C、 $m < n$ D、无法确定

查看试题解析
5. 下表记录了八年级一班甲、乙、丙、丁四名同学最近3次数学模拟测试成绩（满分：120分）的平均数与方差：

甲
乙
丙
丁
平均数
109
108
113
113
方差
4.1
1.0
4.3
0.8
根据表中数据，可知成绩好且发挥稳定的同学是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 如图，在平面直角坐标系中，已知点 $A (- 2 ， 0)$ ， $B (0 ， 3)$ ，以点 $A$ 为圆心， $A B$ 长为半径画弧，交 $x$ 轴的正半轴于点 $C$ ，则点 $C$ 的横坐标为（）

A、 $\sqrt{13} - 2$ B、 $\sqrt{13}$ C、 $\sqrt{13} + 2$ D、 $- \sqrt{13} + 2$

查看试题解析
7. 小明在班上做节约用水意识的调查，收集了班上7位同学家里上个月的用水量（单位：吨）如下：4，4，6，7，8，9，10．他发现，若去掉其中两个数据后，这组数据的中位数，众数保持不变，则去掉的两个数可能是（）

A、4，10 B、4，9 C、7，8 D、6，8

查看试题解析
8. 如图，正方形ABCD的对角线AC，BD交于点O，P为边BC上一点，且BP=OB，则∠COP的度数为（）

A、15° B、22.5° C、 $2 5^{°}$ D、 $17 . 5^{°}$

查看试题解析
9. 如图，菱形 $A B C D$ 的边长为13，对角线 $A C = 24$ ，点E、F分别是边 $C D$ 、 $B C$ 的中点，连接 $E F$ 并延长与 $A B$ 的延长线相交于点G，则 $E G =$ （）

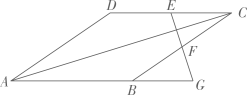A、13 B、10 C、12 D、5

查看试题解析
10. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内现用一个注水管沿大容器内壁匀速注水，如图，则大圆柱形容器水面的高度 $h (c m)$ 与注水时间 $t (m i n)$ 的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 在函数 $y = \sqrt{2 x + 1}$ 中，自变量x的取值范围是 .

查看试题解析
12. 请你写出一个经过点 $(0 ， 1)$ ，且y随x增大而增大的一次函数．

查看试题解析
13. 如图，点A，B，C的坐标分别是 $(0 ， 2)$ ， $(2 ， 2)$ ， $(0 ， - 1)$ ，在第三象限内有一点D使四边形 $A B C D$ 为平行四边形，那么点D的坐标是．

查看试题解析
14. 如图，在 $△ A B C$ 中，D，E分别是 $A B$ ， $A C$ 的中点，点F在 $D E$ 上，且 $∠ A F B = 90 °$ ，若 $A B = 6$ ， $B C = 8$ ，则 $E F$ 的长为．

查看试题解析
15. 如图， $△ A B C$ 和 $△ E C D$ 都是等腰直角三角形， $C A = C B = 2$ ， $C E = C D = 3$ ， $△ A B C$ 的顶点A在 $△ E C D$ 的斜边 $D E$ 上，则 $A E^{2} + A D^{2}$ 的值为．

查看试题解析

三、解答题

16.

(1)、计算： ${(\frac{1}{3})}^{0} + (\sqrt{2} + \sqrt{3})^{2} - \sqrt{8} \times \sqrt{3}$ ．

(2)、先化简，再求值： $(\frac{1}{x - y} + \frac{1}{x + y}) \div \frac{x^{2} y}{x^{2} - y^{2}}$ ，其中 $x = \sqrt{2} + 1$ ， $y = \sqrt{2} - 1$ ．

查看试题解析
17. 如图，在 $▱ A B C D$ 中，连接 $B D$ ．

(1)、实践与操作：利用尺规作对角线 $B D$ 的垂直平分线，分别交 $A D$ ， $B D$ ， $B C$ 于点M，O，N，连接 $B M$ ， $D N$ （要求：保留作图痕迹，标明字母，不写作法）；

(2)、猜想与证明：判断四边形 $B M D N$ 的形状，并说明理由．

查看试题解析

18. 某单位招聘员工，采取笔试与面试结合的方式进行，两项成绩的原始分均为100分．前3名选手的得分如下：

序号项目	$1$	$2$	$3$
笔试成绩/分	$85$	$92$	$84$
面试成绩/分	$90$	$88$	$86$

根据规定，笔试成绩和面试成绩分别按一定的百分比折和成综合成绩（综合成绩的满分仍为100分）

(1)、现得知1号选手的综合成绩为

88

分，求笔试成绩和面试成绩各占的百分比；

(2)、求出其余两名选手的综合成绩，并以综合成绩排好序确定前两名人选．

查看试题解析

19. 大同市拥有完善的能源、重工业产业体系，是国内重要的煤化工、矿山机械等产业基地，具有较强的产业基础和技术优势，本市某企业的一个生产组有工人10名．已知每名工人每天可生产甲种产品12个或乙种产品10个，且每生产一个甲种产品可获得利润100元，每生产一个乙种产品可获得利润180元，在这10名工人中，车间每天安排 $x$ 名工人生产甲种产品，其余工人生产乙种产品．

(1)、求出此车间每天获取利润 $y$ （元）与 $x$ （人）之间的函数解析式；

(2)、若要使此车间每天获取利润不低于15600元，你认为最多派多少名工人去生产甲种产品才合适？

查看试题解析
20. 阅读与思考
下面是小李同学的一篇日记，请仔细阅读并完成相应的任务．
在物理活动课上，我们“博学”小组的同学，进行了“弹簧的长度与外力的变化关系”的探究活动．
第一步：实验测量
多次改变砝码的质量x（克），测量弹簧的长度y（厘米），其中 $0 \leq x \leq 250$ ．
第二步：整理数据

砝码的质量x（克）
0
50
100
150
200
250
弹簧的长度y（厘米）
2
3
4
5
5.5
7
第三步：画函数y关于x的图象
在数据分析时，我发现有一个弹簧的长度是错误的，重新测量后，证明了我的猜想正确，并修改了表中这个数据．
任务：

(1)、表格中错误的数据是， y与x的函数表达式为；

(2)、在平面直角坐标系中，画出y与x的函数图象；

(3)、当弹簧的长度为4.5厘米时，悬挂砝码的质量是多少克，并在图象上描出这个点．

查看试题解析
21. 综合与实践
问题情境：

如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点E，F分别在边 $A D$ ， $B C$ 上，将矩形沿直线 $E F$ 折叠，使点B的对应点 $B^{'}$ 落在 $C D$ 边上，点A的对应点为 $A^{'}$ ，连接 $B B^{'}$ 交 $E F$ 于点O．

问题解决：

(1)、如图①，当点 $B^{'}$ 与点D重合时，求证： $△ F E B^{'}$ 是等腰三角形．

(2)、如图②，当 $D B^{'} = 2$ 时，求 $O F$ 的长．

查看试题解析
22. 综合与探究
如图，在平面直角坐标系中，直线 $y_{1} = - \frac{1}{3} x + \frac{8}{3}$ 与 $x$ 轴， $y$ 轴分别交于点 $B$ ， $A$ ，与直线 $y_{2} = x$ 交于点 $C$ ．

(1)、求点 $C$ 的坐标；

(2)、根据图像，直接写出不等式 $y_{1} \geq y_{2}$ 的解集；

(3)、若点 $D$ 为坐标平面内任意一点，试探究：是否存在点 $D$ ，使 $△ C O D$ 是以 $O C$ 为腰的等腰直角三角形？若存在，请直接写出点 $D$ 的坐标；若不存在，请说明理由．

查看试题解析

砝码的质量x（克）	0	50	100	150	200	250
弹簧的长度y（厘米）	2	3	4	5	5.5	7

	甲	乙	丙	丁
平均数	109	108	113	113
方差	4.1	1.0	4.3	0.8