江西省上饶市余干县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{0.6}$

查看试题解析
2. 以长度分别为下列各组数的线段为边，其中能构成直角三角形的是（）

A、1，2，3 B、2， $\sqrt{2}$ ， $\sqrt{3}$ C、2，3，4 D、3，4，5

查看试题解析
3. 为带动消费提振，拉动经济发展，某区举行炒粉节活动，最终有7位厨师进入决赛，这七位厨师的最后得分分别是：9.5，9.3，9.1，9.4，9.7，9.3，9.6．请问这组评分的众数是（）

A、9.5 B、9.4 C、9.3 D、9.1

查看试题解析
4. 四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，下列条件不能判定这个四边形是平行四边形的是（）

A、 $A B ∥ D C$ ， $A D ∥ B C$ B、 $∠ D A B = ∠ D C B$ ， $∠ A D C = ∠ A B C$ C、 $A O = C O$ ， $B O = D O$ D、 $A B ∥ D C$ ， $A D = B C$

查看试题解析
5. 数形结合是解决数学问题常用的思想方法.如图，直线 $y = 2 x - 1$ 与直线 $y = k x + b (k \neq 0)$ 相交于点 $P (2 ， 3)$ .根据图象可知，关于x的不等式 $2 x - 1 > k x + b$ 的解集是（）

A、 $x < 2$ B、 $x < 3$ C、 $x > 2$ D、 $x > 3$

查看试题解析
6. 如图， $E$ 为正方形 $A B C D$ 对角线 $B D$ 上一点， $F$ 为边 $B C$ 的中点， $E G ⊥ B C$ 于点 $G$ ，若 $A E = E F$ ，下列结论中：① $A E ⊥ E F$ ；② $F G = C G$ ；③ $\frac{S_{△ A B E}}{S_{△ B E G}} = \frac{3}{2}$ ；④ $B E + E D = 2 B F$ ；⑤ $A B + B F = \sqrt{2} B E$ ；正确结论的有（）个

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

7. 若二次根式 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
8. 若一个菱形的两条对角线长分别为10和24，则这个菱形的边长是．

查看试题解析
9. 甲、乙、丙、丁四名射击队员考核赛的平均成绩（环）及方差统计如表，现要根据这些数据，从中选出一人参加比赛，如果你是教练员，你的选择是．
队员
平均成绩（环）
方差
甲
9.7
2.12
乙
9.6
0.56
丙
9.7
0.56
丁
9.6
1.34

查看试题解析
10. 已知点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 是一次函数 $y = (k^{2} + 1) x + 1$ 图象上的两点，当 $x_{1} > x_{2}$ 时， $y_{1}$ $y_{2}$ ．（填“＞”“＝”或“＜”）

查看试题解析
11. 如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH ， EH=12厘米，EF=16厘米，则边AD的长是 cm.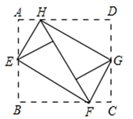

查看试题解析
12. 如图，在平面直角坐标系中已知点 $A (8 ， 0)$ 和点 $B (0 ， 6)$ ， $C$ 是 $A B$ 的中点，若有一动点 $P$ 在折线 $A O B$ 上运动，直线 $C P$ 截 $△ A O B$ 所得的三角形为直角三角形，则点 $P$ 的坐标为．

查看试题解析

三、解答题

13. 计算： $(\sqrt{6} + \sqrt{2}) (\sqrt{6} - \sqrt{2}) - {(\sqrt{3} - 1)}^{2}$

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ 的垂直平分线交 $A D$ 于点 $E$ ，交 $B C$ 于点 $F$ ，连接 $A F$ ， $C E$ ．求证：四边形 $A F C E$ 是菱形．

查看试题解析
15. 阳阳八年级下学期的数学成绩如下表所示：
测验类别
平时测验1
平时测验2
平时测验3
平时测验4
期中考试
期末考试
成绩（分）
108
104
116
112
112
110

(1)、阳阳该学期的数学平时测验的平均成绩分；

(2)、如果学期的综合成绩是根据如图所示的权重计算，请计算出阳阳该学期的数学综合成绩．

查看试题解析
16. 如图，在菱形 $A B C D$ 中，点 $E$ 为 $B C$ 边上一点，请仅用无刻度直尺分别按下列要求画图．（保留画图痕迹）

(1)、在图1中，在 $A D$ 边画出一点 $F$ ，使 $D F = B E$ ；

(2)、在图2中，以 $E$ 为顶点画一个矩形，使得矩形的四个顶点都在菱形的边上．

查看试题解析
17. 如图，已知一次函数y=kx+b的图象经过A(-2，-1)，B(1，3)两点，并且交x轴于点C，交y轴于点D

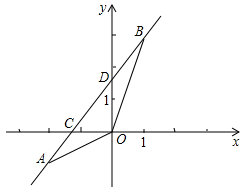(1)、求该一次函数的解析式；

(2)、求△AOB的面积

查看试题解析

18. 炎炎夏日，为了加强学生安全意识，某校开展了“防溺水安全知识竞赛”活动．为了解七、八年级学生（七、八年级各有

600

名学生）的竞赛成绩，现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：

（一）收集数据：

七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77

八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41

（二）整理数据：

	$40 \leq x \leq 49$	$50 \leq x \leq 59$	$60 \leq x \leq 69$		$70 \leq x \leq 79$	$80 \leq x \leq 89$		$90 \leq x \leq 100$
七年级	0	1	0		$a$	7		1
八年级	1	0	0		7	10		2
	平均数			众数			中位数
七年级	78			$b$			78
八年级	78			81			$c$

（三）数据应用：

(1)、由上表填空：

a =

，

b =

，

c =

；

(2)、估计该校七、八年级学生在本次竞赛中成绩在90分以上（含90分）的共有多少人？

(3)、你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好，请说明理由．

查看试题解析

19. 如图学校有一块三角形 $A B C$ 空地，其中 $A C = 10 m$ ， $A B = 17 m$ ， $B C = 21 m$ ，学校计划将这块地建成一个花园，以美化校园，预计花园每平方米造价80元，求学校修建这个花园需要投资多少元？

查看试题解析
20. 为了提升学生在中考体育跳绳成绩，经市场调查，按标价购买 $A$ 种跳绳2条， $B$ 种跳绳5条，则需60元；按标价购买 $A$ 种跳绳1条， $B$ 种跳绳1条，则需18元．

(1)、求 $A$ 种、 $B$ 种跳绳每条标价多少元；

(2)、因需要，班主任王老师计划购进 $A$ ， $B$ 两种跳绳共50条，且购买 $A$ 种跳绳的数量不少于 $B$ 种跳绳数量的2倍．王老师与商店协商：在标价不变的情况下（不考虑其他因素），实际付款总金额按标价九折优惠，请设计一种购买跳绳的方案，使实际所花费用最省，并求出最省的费用．

查看试题解析
21. 阅读理解材料：把分母中的根号化掉叫做分母有理化，例如：① $\frac{1}{\sqrt{5}} = \frac{1 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} = \frac{\sqrt{5}}{5}$ ；② $\frac{1}{\sqrt{2} - 1} = \frac{1 \times (\sqrt{2} + 1)}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \frac{\sqrt{2} + 1}{{(\sqrt{2})}^{2} - 1^{2}} = \sqrt{2} + 1$ 等运算都是分母有理化．
根据上述材料，

(1)、化简： $\frac{1}{2 \sqrt{3}}$ ；

(2)、化简： $\frac{1}{\sqrt{5} - \sqrt{3}}$ ；

(3)、计算： $(\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \cdot \cdot \cdot + \frac{1}{\sqrt{2023} + \sqrt{2021}}) (\sqrt{2023} + 1)$ ．

查看试题解析
22.

(1)、方法回顾
在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：

第一步添加辅助线：如图1，在 $△ A B C$ 中，延长 $D E$ （ $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 的中点）到点 $F$ ，使得 $E F = D E$ ，连接 $C F$ ；

第二步证明 $△ A D E ≌ △ C F E$ （依据▲  ），

易证： $B D = C F$ ， $B D ∥ C F$ ，再证四边形 $D B C F$ 是平行四边形（依据▲ ）

从而得到中位线 $D E$ 与 $B C$ 的关系；位置关系▲  ，数量关系▲  ；

(2)、问题解决
如图2，在正方形 $A B C D$ 中， $E$ 为 $A D$ 的中点， $G$ 、 $F$ 分别为 $A B$ 、 $C D$ 边上的点，若 $A G = 2$ ， $A D = 6$ ， $∠ G E F = 90 °$ ，求 $G F$ 的长．



查看试题解析
23. 如图，在平面直角坐标系中，已知直线 $l_{1}$ ： $y = k x + 4$ 经过 $A (2 ， 0)$ ，动点 $P$ 在直线 $l_{2}$ ： $y = 2 x + 2$ 上，直线 $l_{1}$ 和 $l_{2}$ 交于点 $B$ ，设点 $P$ 的横坐标为 $m$ ，

(1)、求 $k$ 的值和点 $B$ 的坐标．

(2)、过点 $P$ 作 $x$ 轴的平行线交直线 $l_{1}$ 于点 $Q$ ，当以 $O$ 、 $A$ 、 $P$ 、 $Q$ 为顶点的四边形为平行四边形时，求 $m$ 的值；

(3)、过点 $P$ 作 $x$ 轴的垂线交 $x$ 轴于点 $M$ ，以 $P M$ 为边向右作正方形 $P M N C$ ，当正方形 $P M N C$ 的顶点 $N$ 或 $C$ 落在直线 $l_{1}$ 上时，直接写出 $m$ 的值．

查看试题解析

队员	平均成绩（环）	方差
甲	9.7	2.12
乙	9.6	0.56
丙	9.7	0.56
丁	9.6	1.34

测验类别	平时测验1	平时测验2	平时测验3	平时测验4	期中考试	期末考试
成绩（分）	108	104	116	112	112	110