江西省九江市2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列各式中一定成立的是( )A、 B、 C、 D、3. 若分式的值为0,则( )A、 B、 C、 D、或24. 如图,的对角线相交于点 , 且 , , 则的周长是( )
2. 若 , 则下列各式中一定成立的是( )A、 B、 C、 D、3. 若分式的值为0,则( )A、 B、 C、 D、或24. 如图,的对角线相交于点 , 且 , , 则的周长是( )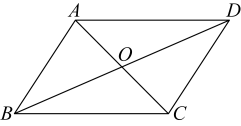 A、9 B、10 C、11 D、125. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交 , 于点 , 再分别以点为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( )
A、9 B、10 C、11 D、125. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交 , 于点 , 再分别以点为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( ) A、15 B、30 C、45 D、606. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )
A、15 B、30 C、45 D、606. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )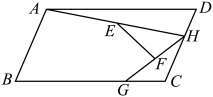 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
7. 因式分解: .8. 正六边形的每个内角等于°.9. 如图:已知直线 , 点在上,点在上,若的面积为27,且 , 则平行线与之间的距离为 .
 10. 如图,点P为三边垂直平分线的交点,若 , , 则的度数为 .
10. 如图,点P为三边垂直平分线的交点,若 , , 则的度数为 . 11. 如图,直线与相交于点P , 已知点P的坐标为 , 则关于的不等式的解集是 .
11. 如图,直线与相交于点P , 已知点P的坐标为 , 则关于的不等式的解集是 . 12. 已知中, , , 若沿射线方向平移m个单位得到 , 顶点A , B , C分别与顶点D , E , F对应,若以点A , D , E为顶点的三角形是等腰三角形,则m的值是 .
12. 已知中, , , 若沿射线方向平移m个单位得到 , 顶点A , B , C分别与顶点D , E , F对应,若以点A , D , E为顶点的三角形是等腰三角形,则m的值是 .三、解答题
-
13.(1)、因式分解(2)、化简14. 解不等式组: ,并把解集在数轴上表示出来.15. 解分式方程: .16. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,的顶点均在格点上.
 (1)、画出关于y轴对称的;(2)、画出将绕原点O顺时针旋转90°所得的;17. 如图,在中, , 是边上的中线,于E , 求证: .
(1)、画出关于y轴对称的;(2)、画出将绕原点O顺时针旋转90°所得的;17. 如图,在中, , 是边上的中线,于E , 求证: . 18. 先化简,再求值: ,其中x是从1,2,3中选取的一个合适的数.19. 某工厂购买一批原材料,通过汽车运输每吨只需运费800元,由货船运输每吨需运费300元,但运完这批原材料需要其它费用15000元.(1)、设购买的原材料x吨,选择汽车运输时所需费用元,选择货船运输时所需费用元,分别写出、与x之间的关系式;(2)、请分析说明选择哪种运输方式比较合理.20. 如图,四边形为平行四边形,为上的一点,连结并延长,使 , 连结并延长,使 , 连结 . 为的中点,连结 .
18. 先化简,再求值: ,其中x是从1,2,3中选取的一个合适的数.19. 某工厂购买一批原材料,通过汽车运输每吨只需运费800元,由货船运输每吨需运费300元,但运完这批原材料需要其它费用15000元.(1)、设购买的原材料x吨,选择汽车运输时所需费用元,选择货船运输时所需费用元,分别写出、与x之间的关系式;(2)、请分析说明选择哪种运输方式比较合理.20. 如图,四边形为平行四边形,为上的一点,连结并延长,使 , 连结并延长,使 , 连结 . 为的中点,连结 . (1)、求证:四边形为平行四边形;(2)、若 , , , 求的度数.21. 某服装店用6000元购进一批衬衫,很快售完,服装店老板又用2800元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2600元,则第二批衬衫每件至少要售多少元?
(1)、求证:四边形为平行四边形;(2)、若 , , , 求的度数.21. 某服装店用6000元购进一批衬衫,很快售完,服装店老板又用2800元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2600元,则第二批衬衫每件至少要售多少元?

