江西省上饶市鄱阳县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 某组7名同学在一学期里阅读课外书籍的册数分别是:14,12,13,12,17,18,16.则这组数据的众数和中位数分别是( )A、12,13 B、12,14 C、13,14 D、13,162. 一直角三角形的斜边长比一直角边长大2,另一直角边长为6,则斜边长为( )A、4 B、8 C、10 D、123. 函数 的自变量x的取值范围为A、 B、 C、 D、 且4. 如图,已知菱形 的对角线 , 的长分别为6cm,8cm, 于点 ,则 的长是( )
 A、 B、 C、 D、5. 设实数a,b在数轴上对应的位置如图所示,化简 +|a+b|的结果是( )
A、 B、 C、 D、5. 设实数a,b在数轴上对应的位置如图所示,化简 +|a+b|的结果是( ) A、-2a+b B、2a+b C、-b D、b6. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
A、-2a+b B、2a+b C、-b D、b6. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )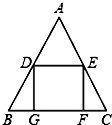 A、 cm B、4cm C、 cm D、2 cm
A、 cm B、4cm C、 cm D、2 cm二、填空题
-
7. 计算: .8. 请根据如图所示的函数图象,求方程组解为 .
 9. 某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如表:
9. 某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如表:时间(单位:小时)
4
3
2
1
0
人数
2
4
2
1
1
则这10名学生周末利用网络进行学习的平均时间是小时.
10. 已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1),则此函数的解析式为 .11. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .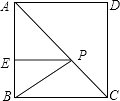 12. 在△ABC中,AB=2 ,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 .
12. 在△ABC中,AB=2 ,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 .
三、解答题
-
13. 解答(1)、计算: .(2)、如图,在四边形中, , . 求证:四边形是平行四边形.
 14. 先化简,再求值:÷(1+),其中x=-(π-3)0.15. 已知与成正比例,且时, .(1)、求y与x之间的函数关系式,并指出它是什么函数;(2)、若点在这个函数的图象上,求a的值.16. 如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
14. 先化简,再求值:÷(1+),其中x=-(π-3)0.15. 已知与成正比例,且时, .(1)、求y与x之间的函数关系式,并指出它是什么函数;(2)、若点在这个函数的图象上,求a的值.16. 如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图: (1)、在图①中画一条线段MN , 使MN= ;(2)、在图②中画一个三边长均为无理数,且各边都不相等的直角△DEF .17. 在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?18. 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,垂足分别为点E,F.
(1)、在图①中画一条线段MN , 使MN= ;(2)、在图②中画一个三边长均为无理数,且各边都不相等的直角△DEF .17. 在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?18. 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,垂足分别为点E,F. (1)、求证:BE=BF;(2)、当菱形ABCD的对角线AC=8,BD=6时,求BE的长.19. 四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(1)、求证:BE=BF;(2)、当菱形ABCD的对角线AC=8,BD=6时,求BE的长.19. 四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题: (1)、本次接受随机抽样调查的学生人数为 , 图①中m的值是;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、根据样本数据,估计该校本次活动捐款金额为10元的学生人数.20. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为 A(-3,0),与y轴交点为B , 且与正比例函数的图象的交于点 C(m , 4).
(1)、本次接受随机抽样调查的学生人数为 , 图①中m的值是;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、根据样本数据,估计该校本次活动捐款金额为10元的学生人数.20. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为 A(-3,0),与y轴交点为B , 且与正比例函数的图象的交于点 C(m , 4). 、(1)、求m的值及一次函数 y=kx+b的表达式;(2)、若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.21. 甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.
、(1)、求m的值及一次函数 y=kx+b的表达式;(2)、若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.21. 甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.
 (1)、A、B两地的距离千米;乙车速度是;a表示 .(2)、乙出发多长时间后两车相距330千米?22. 观察下列各式及其验算过程:
(1)、A、B两地的距离千米;乙车速度是;a表示 .(2)、乙出发多长时间后两车相距330千米?22. 观察下列各式及其验算过程:验证:
验证:
按照上述两个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
针对上述各式反映的规律,写出用(为任意自然数,且)表示的等式,并给出证明.
23. 某数学兴趣小组开展了一次课外活动,过程如下:如图1,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q. (1)、求证:DP=DQ;(2)、如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)、如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
(1)、求证:DP=DQ;(2)、如图2,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)、如图3,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.