江西省吉安市吉安县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若x>y，则下列式子中错误的是（）

A、x－3>y－3 B、 $\frac{x}{3} > \frac{y}{3}$ C、x+3>y+3 D、－3x>－3y

查看试题解析
3. 下列因式分解正确的是（）

A、 $x^{2} - x = x (x + 1)$ B、 $a^{2} - 3 a - 4 = (a + 4) (a - 1)$ C、 $x^{2} - y^{2} = (x + y) (x - y)$ D、 $a^{2} + 2 a b - b^{2} = {(a - b)}^{2}$

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， ED是AB的垂直平分线，交AC于点D ，交AB于E ，已知 $∠ C B D = 10 °$ ，则 $∠ A$ 的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
5. 工人常用角尺平分一个任意角，做法如下：如图： $∠ A O B$ 是一个任意角，在边 $O A 、 O B$ 上分别取 $O M = O N$ ，移动角尺，使角尺两边相间的刻度分别与点M、N重合，过角尺顶点C作射线 $O C$ ，由此作法便可得 $△ N O C ≌ △ M O C$ 其依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
6. 如图，在△ABC中， $A B = 3$ ， $A C = 4$ ， $B C = 5$ ， △ABD ， △ACE ， △BCF都是等边三角形，下列结论中：① $A B ⊥ A C$ ；②四边形AEFD是平行四边形；③ $∠ D F E = 150 °$ ；④ $S_{四边形 A E F D} = 6$ ．正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 分解因式： $a^{2} b - a^{3} =$ ．

查看试题解析
8. 若2y﹣5x＝0，则x：y＝．

查看试题解析
9. 点 $P (- 1 ， - 3)$ 向左平移m个单位长度，再向上平移的n个单位长度所得对应点为 $Q (- 2 ， 0)$ ，则 $m + n =$ ．

查看试题解析
10. 如图，数轴上所表示关于x的不等式组的解集．

查看试题解析
11. 如图，下列4个结论① $∠ 1 + ∠ 2 > ∠ 3 + ∠ 4$ ， ② $∠ 1 + ∠ 2 = ∠ 3 + ∠ 4$ ， ③ $∠ 1 + ∠ 2 < ∠ 3 + ∠ 4$ ， ④无法比较以上四个角的大小，正确的是．（填序号）

查看试题解析
12. 在平面直角坐标系中，已知点 $A (4 ， 0)$ ，点 $B (- 3 ， 2)$ ，点 $C (0 ， 2)$ ，点 $Р$ 从点 $B$ 出发，以 $2$ 个单位每秒的速度沿射线 $B C$ 运动，点 $Q$ 从点 $A$ 出发，开始以 $1$ 个单位每秒的速度向原点 $О$ 运动，到达原点后立刻以原来 $3$ 倍的速度沿射线 $O A$ 运动，若 $P ， Q$ 两点同时出发，设运动时间为 $t$ 秒，则当 $t =$ 时，以点 $A ， Q ， C ， P$ 为顶点的四边形为平行四边形．

查看试题解析

三、解答题

13.

(1)、因式分解： $m a^{2} - 4 m b^{2}$

(2)、解方程： $\frac{1}{x - 2} = \frac{3}{x}$

查看试题解析
14. 解不等式组 ${\begin{array}{l} 2 x - 1 > 0 ， \\ \frac{1}{2} (x + 4) < 3 . \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
15. 关于x的方程 $\frac{m}{x^{2} - 4} + \frac{2}{x + 2} = \frac{1}{x - 2}$ 有增根，则增根是多少？并求方程产生增根时m的值．

查看试题解析
16. 例在 $▱ A B C D$ 中，点E为AB上一点，请仅用无刻度直尺按要求作图（保留作图痕迹，不写作法，题目要求画的线画实线，其他的线画虚线）

(1)、如图1，E为 $A B$ 边上一点， $A E = A D$ ，画出∠D的角平分线；

(2)、如图2，E为 $A B$ 边上一点， $A E = A D$ ，画出∠B的角平分线．

查看试题解析
17. 先化简 $\frac{x^{2} - 4 x + 4}{x^{2} - 1} \div \frac{x^{2} - 2 x}{x + 1} + \frac{1}{x - 1}$ ，再从 $- 2 \leq x \leq 2$ 中选一个合适的整数作为x的值代入求值．

查看试题解析
18. 某学校后勤人员到一家文具店给九年级的同学购买考试用文具包，文具店规定一次购买400个以上，可享受8折优惠，若给九年级学生每人购买一个，不能享受8折优惠，需付款1 936元；若多买88个，就可享受8折优惠，同样只需付款1 936元，请问该学校九年级学生有多少人？

查看试题解析
19. 四边形ABCD中，已知AB∥DC，DB平分∠ADC，∠ADC＝∠C＝60°，延长CD到点E，连结AE，使得∠C＝2∠E．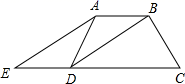

(1)、试判断四边形ABDE的形状，并说明理由；

(2)、若AB＝8，求CD的长．

查看试题解析
20. 常用的分解因式的方法有提取公因式法、公式法及到了高中还要学习的十字相乘法，但有更多的多项式只用上述方法就无法分解，如 $x^{2} - 4 y^{2} - 2 x + 4 y$ ，我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了．过程为：
$x^{2} - 4 y^{2} - 2 x + 4 y = (x + 2 y) (x - 2 y) - 2 (x - 2 y) = (x - 2 y) (x + 2 y - 2)$

这种分解因式的方法叫分组分解法．利用这种方法解决下列问题：

(1)、分解因式 $a^{2} - 4 a - b^{2} + 4$ ；

(2)、 $△ A B C$ 三边 $a ， b ， c$ 满足 $a^{2} - a b - a c + b c = 0$ ，判断 $△ A B C$ 的形状．

查看试题解析
21. 如图所示，根据图中信息．

(1)、 $m =$ ； $n =$ ；点P的坐标为．

(2)、当x为何值时， $y_{1} > y_{2}$ ？

(3)、求 $S_{△ A P B}$ ．

查看试题解析
22. 如图，在 $▱ A B C D$ 中， $A B = 12 c m$ ， $B C = 6 c m$ ， $∠ A = 60 °$ ，点P沿AB边从点A开始以2cm秒的速度向点B移动，同时点Q沿DA边从点D开始以1cm/秒的速度向点A移动，用t表示移动的时间 $(0 \leq t \leq 6)$ ．

(1)、当t为何值时，△PAQ是等边三角形．

(2)、当t为何值时，△PAQ为直角三角形．

查看试题解析
23. 类比、转化等数学思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．
已知△ABC ．

(1)、观察发现
如图①，若点D是 $∠ A B C$ 和 $∠ A C B$ 的角平分线的交点，过点D作 $E F ∥ B C$ 分别交 $A B$ ， $A C$ 于E ， F ．填空： $E F$ 与 $B E 、 C F$ 的数量关系是．请说明理由

(2)、猜想论证
如图②，若点D是外角 $∠ C B E$ 和 $∠ B C F$ 的角平分线的交点，其他条件不变，填： $E F$ 与 $B E 、 C F$ 的数量关系是．请说明理由

(3)、类比探究
如图③，若点D是 $∠ A B C$ 和外角 $∠ A C G$ 的角平分线的交点．其他条件不变，则（1）中的关系成立吗？若成立，请加以证明；若不成立，请写出关系式，再证明．

查看试题解析