湖南省长沙市长郡集团2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，是一次函数的是（）

A、 $y = x - 1$ B、 $y = k x + b$ C、 $y = \frac{2}{x}$ D、 $y = - 2 x^{2} + 1$

查看试题解析
2. 已知关于x的一元二次方程x²＋bx＋1＝0有两个不相等的实数根，则在下列选项中，b的值可以是（）

A、b＝-1 B、b＝-2 C、b＝-3 D、b＝0

查看试题解析
3. 如图， $▱ A B C D$ 的对角线 $A C ， B D$ 相交于点O ， E是 $A B$ 上一点，且 $A E = B E = 2$ ， $E O = 3$ ，则 $▱ A B C D$ 的周长为（）

A、20 B、16 C、12 D、8

查看试题解析
4. 如图是甲、乙两射击运动员的10次射击训练成绩（环数）的折线统计图，观察图形，甲、乙这10次射击成绩的方差 $S_{甲}^{2}$ ， $S_{乙}^{2}$ 之间的大小关系是（）

A、 $S_{甲}^{2} < S_{乙}^{2}$ B、 $S_{甲}^{2} > S_{乙}^{2}$ C、 $S_{甲}^{2} = S_{乙}^{2}$ D、不能确定

查看试题解析
5. 下列命题是真命题的是（）

A、对角线相等且互相平分的四边形是矩形 B、对角线相等的四边形是矩形 C、平行四边形的对角线互相垂直 D、对角线互相垂直的四边形是菱形

查看试题解析
6. 一元二次方程 $x^{2} - 2 x + a = 0$ 的一根是 $3$ ，则另外一根是（）

A、 $3$ B、 $1$ C、 $- 3$ D、 $- 1$

查看试题解析
7. 在平面直角坐标系中，将一次函数 $y = m x - 1$ （m是常数）的图象向下平移2个单位长度后经过点 $(- 2 ， 1)$ ，则m的值为（　　）

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
8. 已知点 $(k ， b)$ 为第一象限内的点，则一次函数 $y = k x - b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 某油箱容量为 $50 L$ 的汽车，加满汽油后行驶了 $100 k m$ 时，油箱中的汽油大约消耗了 $\frac{1}{5}$ ，如果加满汽油后汽车行驶的路程为 $x k m$ ，油箱中剩油量为 $y L$ ，则y与x之间的函数解析式和自变量取值范围分别是（）

A、 $y = 0.1 x$ ， $x > 0$ B、 $y = 50 - 0.1 x$ ， $x > 0$ C、 $y = 0.1 x$ ， $0 \leq x \leq 500$ D、 $y = 50 - 0.1 x$ ， $0 \leq x \leq 500$

查看试题解析
10. 如图，函数 $y = k x + b (k \neq 0)$ 的图象经过点 $B (3 ， 0)$ ，与函数 $y = 2 x$ 的图象交于点A ，则不等式 $0 < k x + b < 2 x$ 的解集为（）

A、 $x > 0$ B、 $0 < x < 1$ C、 $1 < x < 3$ D、 $x > 3$

查看试题解析
11. 代数式 $x^{2} - 4 x + 5$ 的最小值为（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
12. 如图，菱形 $A B C D$ 中， $A B = 2$ ， $∠ A = 120 °$ ，点P ， Q ， K分别为线段 $B C ， C D ， B D$ 上的任意一点，则 $P K + Q K$ 的最小值为（）．

A、1 B、 $\sqrt{3}$ C、2 D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析

二、填空题

13. 当 $m =$ 时，关于 $x$ 的方程 $(m + 2) x^{m + 3} + 6 x - 9 = 0$ 是一元二次方程．

查看试题解析
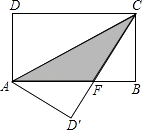
14. 东方红学校规定：学生的学期体育成绩满分为100分，其中早锻炼及体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%．小聪的三项成绩依次是85分，90分，92分，则小聪这学期的体育成绩是分．

查看试题解析
15. 已知方程 $3 x^{2} - 2 x - 4 = 0$ 的两根分别为 $x_{1}$ 和 $x_{2}$ ，则 $x_{1} x_{2} =$ ．

查看试题解析
16. 上数学课时，老师给出一个函数，让同学们指出它的性质．甲说函数图象不经过第三象限；乙说函数图象经过第一象限；丙说 $x < 0$ 时，y随x的增大而减少；丁说 $x > 1$ 时， $y < 0$ ．已知这四位同学说的都正确，请你写出符合上述性质的一个函数解析式．

查看试题解析
17. 如图，矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为．

查看试题解析
18. 如图，四边形 $A B C D$ 是正方形，点 $E$ 在边 $A D$ 上， $△ B E F$ 是以 $E$ 为直角顶点的等腰直角三角形， $E F$ ， $B F$ 分别交 $C D$ 于点 $M$ ， $N$ ，过点 $F$ 作 $A D$ 的垂线交 $A D$ 的延长线于点 $G$ ．连接 $D F$ ，请完成下列问题：

(1)、 $∠ F D G =$ ；

(2)、若 $D E = 1$ ， $D F = \sqrt{2}$ ，则 $M C =$ ．

查看试题解析

三、解答题

19. 用合适的方法解下列一元二次方程．

(1)、 $2 x^{2} - 8 = 0$ ；

(2)、 $x^{2} - 2 (x + 4) = 0$ ．

查看试题解析

20. “青年大学习”是共青团中央为组织引导广大青少年，深入学习贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学校行动，我校为了解学生某季度学习“青年大学习”的情况，从中随机抽取20位同学，并统计学习时间（学习时间用x表示，单位：分钟）收集数据如下：

30 56 80 30 40 110 120 156 90 120

58 80 120 140 70 84 10 20 100 86

整理数据：按如下分段整理样本数据并补全表格．

学习时间x（分钟）	$0 \leq x < 10$	$40 \leq x < 80$	$80 \leq x < 120$	$120 \leq x \leq 160$
人数	4	a	7	b

分析数据：补全下列表格中的统计量．

平均数	中位数	众数
80	c	d

(1)、直接写出上述表格中

a ， b ， c ， d

的值；

(2)、我校有1600名同学参加了此次调查活动，请估计学习时间不低于80分钟的人数是多少？

查看试题解析

21. 已知一次函数 $y = k x + b$ 的图象与y轴交于点 $A (0 ， 4)$ ，且过点 $B (2 ， 3)$ ．

(1)、求一次函数的解析式；

(2)、若点P为该一次函数上的一点，且点C为该函数图象与x轴的交点，若 $S_{△ P C O} = 10$ ，求点P的坐标．

查看试题解析
22. 如图，平行四边形 $A B C D$ 中， $A D = B D$ ，过点 $C$ 作 $C E ∥ B D$ ，交 $A D$ 的延长线于点 $E$ ．

(1)、求证：四边形 $B D E C$ 是菱形；

(2)、连接 $B E$ ，若 $A B = 6$ ， $A D = 12$ ，求 $B E$ 的长．

查看试题解析
23. 建设美丽城市，改造老旧小区.某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同.

(1)、求该市改造老旧小区投入资金的年平均增长率；

(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质，每个小区改造费用增加15%.如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？

查看试题解析
24. 某超市欲购进A ， B两种品牌的书包共500个．已知两种书包的进价和售价如下表所示．设购进A种书包x个，且所购进的两种书包能全部卖出，获得的总利润为w元．
品牌
进价（元/个）
售价（元/个）
A
57
75
B
47
60

(1)、求w关于x的函数关系式；

(2)、如果购进两种书包的总费用不超过28000元，那么商场如何进货才能获利最大？并求出最大利润．

查看试题解析
25. 我们不妨约定：在平面直角坐标系中，将点 $P (2 ， 1)$ 称为“幸福点”，经过点 $P (2 ， 1)$ 的函数，称为“幸福函数”．

(1)、若点 $(3 r + 4 s ， 2 r + s)$ 是“幸福点”，关于x的函数 $y = x + t$ 是“幸福函数”，则 $r =$ ， $s =$ ， $t =$ ．

(2)、若关于x的函数 $y = k x + b$ 和 $y = \frac{m}{x}$ 都是“幸福函数”，且两个函数图象有且只有一个交点，求k的值．

(3)、若直线 $y = - \frac{4}{3} x + 4 b (b > 0)$ 与x轴、y轴分别交于点A ， B ， M是y轴上一点，若将 $△ A B M$ 沿直线AM折叠，点B恰好落在x轴上的点C处．试问经过C ， M两点的一次函数是否可以为“幸福函数”？若可以，请写出所有函数解析式；若不可以，请说明理由．

查看试题解析
26. 如图，在直角坐标系中，直线 $y = \sqrt{3} x - 2 \sqrt{3}$ 交y轴，x轴于点 $A ， B$ ，点D在y轴正半轴上，以 $A B ， A D$ 为边作平行四边形ABCD ，点E从点O出发，以每秒1个单位的速度沿y轴正方向移动，记点E运动时间为t秒．

(1)、直接写出点A的坐标， $A B =$ ；

(2)、若 $O D = 2 O A$ ，连接 $B D ，$ F是 $B D$ 的中点，连接 $E F$ 并延长交直线 $B C$ 于点H ，
①当四边形 $A B H E$ 为平行四边形时，请直接写出t的值；
②当 $△ B F H$ 是以 $B F$ 为腰的等腰三角形时，请直接写出t的值；

(3)、若 $A D = 4 \sqrt{3}$ ，点E在 $O D$ 上，点M位于点E的正上方，且 $∠ E B C + ∠ M C B = 90 °$ ，当四边形 $E B C M$ 的面积最大时，求 $D M$ 的长．

查看试题解析

品牌	进价（元/个）	售价（元/个）
A	57	75
B	47	60