江西省吉安市青原区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-08-16 类型:期末考试
一、单选题
-
1. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、
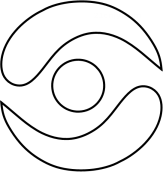 B、
B、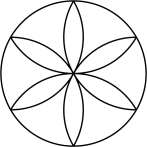 C、
C、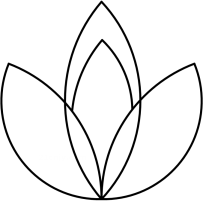 D、
D、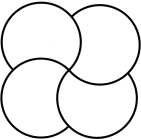 2. 要使有意义,则x的取值范围为( )A、 B、 C、 D、3. 下列从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 如图,在中, , 点是边上的一点,点是的中点,若的垂直平分线经过点 , , 则( )
2. 要使有意义,则x的取值范围为( )A、 B、 C、 D、3. 下列从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 如图,在中, , 点是边上的一点,点是的中点,若的垂直平分线经过点 , , 则( )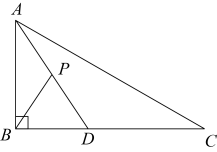 A、8 B、6 C、4 D、25. 如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A、8 B、6 C、4 D、25. 如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )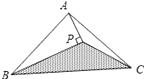 A、2cm2 B、3cm2 C、4cm2 D、5cm26. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3 , 使得A2A3=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为( )
A、2cm2 B、3cm2 C、4cm2 D、5cm26. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3 , 使得A2A3=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为( )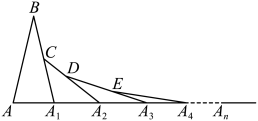 A、5° B、10° C、15° D、25°
A、5° B、10° C、15° D、25°二、填空题
-
7. 分解因式:m2﹣2m= .8. 若点和点关于x轴对称,则 的值是 .9. 一个多边形的内角和是它的外角和的4.5倍,这个多边形的边数是 .10. 如图,∠AOP=∠BOP,PC∥OA,PD⊥OA,若∠AOB=45°,PC=6,则PD的长为 .
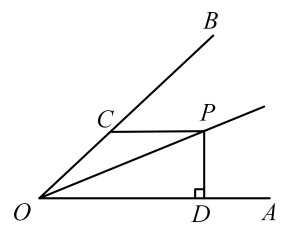 11. 如图,直线与直线相交于点 , 则不等式的解集是 .
11. 如图,直线与直线相交于点 , 则不等式的解集是 .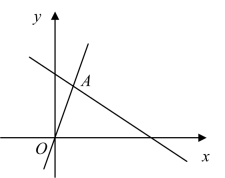 12. 如图,中, , , , 动点从点出发沿射线以的速度运动,设运动时间为 , 当为等腰三角形时,的值为 .
12. 如图,中, , , , 动点从点出发沿射线以的速度运动,设运动时间为 , 当为等腰三角形时,的值为 .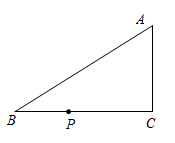
三、解答题
-
13.(1)、因式分解:;(2)、解方程: .14. 先化简,再求值: , 其中15. 如图,在中,分别在边上,且 , 求证:四边形是平行四边形.
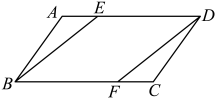 16. 解不等式组: , 并把它的解集在数轴上表示出来.17. 如图,四边形ABCD为正方形,点E在边BC上.请仅用无刻度直尺完成以下作图(保留作图痕迹).
16. 解不等式组: , 并把它的解集在数轴上表示出来.17. 如图,四边形ABCD为正方形,点E在边BC上.请仅用无刻度直尺完成以下作图(保留作图痕迹).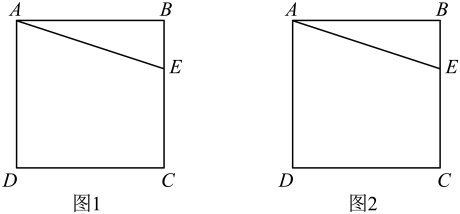 (1)、在图1中,以AE为边,在正方形ABCD内作一个平行四边形;(2)、在图2中,以AE为边,在正方形ABCD内作一个等腰三角形.18. 如图,已知中,垂直平分交于点 , 交于点 , 连接 .
(1)、在图1中,以AE为边,在正方形ABCD内作一个平行四边形;(2)、在图2中,以AE为边,在正方形ABCD内作一个等腰三角形.18. 如图,已知中,垂直平分交于点 , 交于点 , 连接 .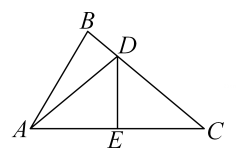 (1)、若 , , 求的度数;(2)、若 , , 求的周长.19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1) .
(1)、若 , , 求的度数;(2)、若 , , 求的周长.19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1) .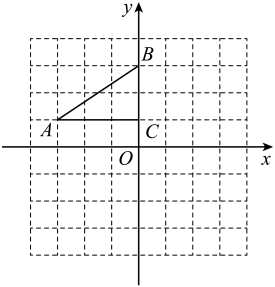 (1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;(2)、分别连接AB1 , BA1后,求四边形AB1A1B的面积 .20. “双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动时间,现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳个数和用500元购买的毽子数量相同.(1)、求跳绳和毽子的单价分别是多少元?(2)、由于库存较大,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七折出售.学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于460根,请你求出学校花钱最少的购买方案.21. 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;(2)、分别连接AB1 , BA1后,求四边形AB1A1B的面积 .20. “双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动时间,现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳个数和用500元购买的毽子数量相同.(1)、求跳绳和毽子的单价分别是多少元?(2)、由于库存较大,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七折出售.学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于460根,请你求出学校花钱最少的购买方案.21. 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
 (1)、求证:BE=CD;(2)、连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.22. 阅读下面的材料,回答问题:如果 , 求的取值范围.
(1)、求证:BE=CD;(2)、连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.22. 阅读下面的材料,回答问题:如果 , 求的取值范围.解:根据“两数相乘,同号得正,异号得负”,得或 , 分别解这两个不等式组,得第一个不等式组的解集为 , 第二个不等式组的解集为 . 故当或时, .
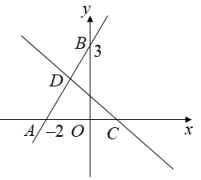 (1)、试利用上述方法,求不等式的解集.(2)、如图,直线与轴交于点 , 直线与轴交于点 , 根据图象,请你直接写出关于的不等式的解集.23. 如图,在四边形ABCD中,∠B=60°,AB=DC=4,AD=BC=8,延长BC到E,使CE=4,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒(t>0).
(1)、试利用上述方法,求不等式的解集.(2)、如图,直线与轴交于点 , 直线与轴交于点 , 根据图象,请你直接写出关于的不等式的解集.23. 如图,在四边形ABCD中,∠B=60°,AB=DC=4,AD=BC=8,延长BC到E,使CE=4,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒(t>0). (1)、当t=3时,BP=;(2)、当t=时,点P运动到∠B的角平分线上;(3)、当0<t<6时,请用含t的代数式表示△ABP的面积S;(4)、当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
(1)、当t=3时,BP=;(2)、当t=时,点P运动到∠B的角平分线上;(3)、当0<t<6时,请用含t的代数式表示△ABP的面积S;(4)、当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.