江西省吉安市遂川县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{3}{x - 2}$ 有意义，则x的取值范围是（）

A、x>2； B、x<2； C、 $x \neq - 2$ ； D、 $x \neq 2$ ；

查看试题解析
2. 若 $a > b$ ，那么下列各式中正确的是（　　）

A、 $a - 1 < b - 1$ B、 $- a > - b$ C、 $\frac{a}{2} < \frac{b}{2}$ D、 $- 2 a < - 2 b$

查看试题解析
3. 观察下列图形，是中心对称图形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列因式分解正确的是（）

A、 $a^{2} - 4 a b + 4 b^{2} = {(a - 2 b)}^{2}$ B、 $x^{2} + 4 y^{2} = {(x + 2 y)}^{2}$ C、 $a^{2} - b^{2} = {(a - b)}^{2}$ D、 $2 a b^{2} - 4 a^{2} b = a b (2 b - 4 a)$

查看试题解析
5. 如图，在平行四边形 $A B C D$ 中， $A E$ 平分 $∠ B A D$ ，若 $∠ D = 58 °$ ，则 $∠ E A B$ 的度数是（）

A、58° B、59° C、60° D、61°

查看试题解析
6. 如图（1），将一副直角三角板两斜边摆放在同一直线上，且点 $A$ ， $D$ 重合，固定含 $45 °$ 角的三角板 $A B C$ ，将含 $30 °$ 角的三角板 $D E F$ 从图（ $1$ ）的位置，沿射线 $B A$ 平移至图（ $2$ ）的位置，则平移过程中，根据两个三角板的摆放位置，下列钝角： $100 °$ ， $105 °$ ， $120 °$ ， $135 °$ ， $150 °$ ， $165 °$ ， $170 °$ ，沿三角板的边缘能直接画出的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 若x小于y ，则 $x - y$ 是数（填“正”或“负”）.

查看试题解析
8. 多项式 $4 x (m - n) + 2 y (m - n)^{2}$ 的公因式是．

查看试题解析
9. 在平面直角坐标系中，点 $(- 2 ， 0)$ 绕原点 $O$ 点顺时针旋转 $90 °$ 后所得点的坐标是.

查看试题解析
10. 化简 $\frac{x^{2}}{x - 2} - \frac{2 x}{x - 2}$ 的结果是.

查看试题解析
11. 如图，在等边 $△ A B C$ 中， $A B = 6$ ， $A D ⊥ B C$ ， E是AC上的一点，M是AD上的点，若 $A E = 2$ ，求 $M E + M C$ 的最小值．

查看试题解析
12. 如图，等腰三角形纸片ABC中， $A D ⊥ B C$ 于点D ， $B C = 4$ ， $A D = 3$ ，沿AD剪成两个三角形.用这两个三角形拼成平行四边形，该平行四边形较长对角线的长为.

查看试题解析

三、解答题

13. 计算

(1)、分解因式： $2 x^{3} - 8 x$ ；

(2)、一个多边形的内角是 $1080 °$ ，求多边形的边数.

查看试题解析
14. 解不等式组 ${\begin{array}{l} x + 1 < 5 \\ 2 (x + 4) > 3 x + 7 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
15. 如图，在 $□ A B C D$ 中，E ， F分别在 $A B ， C D$ 上， $E F$ 交 $A C$ 于点O ，若 $B E = D F$ ，求证：点O为 $A C$ 的中点．

查看试题解析
16. 先化简，再求值： $(1 - \frac{1}{a + 1}) \div \frac{a^{2} - 2 a + 1}{a^{2} - 1}$ ，其中 $a = - 2$ .

查看试题解析
17. 如图，在正方形网格中， $△ A B C$ 的顶点在格点上.请仅用无刻度直尺完成以下作图（保留作图痕迹）.

(1)、在图1中，把 $△ A B C$ 平移，使点B平移后与点C重合，作出平移后的三角形；

(2)、在图2中，把 $△ A B C$ 绕点A顺时针旋转一定角度，顶点仍在格点上，作出旋转后的三角形.

查看试题解析
18. 为落实“乡村振兴计划”的工作要求，某乡镇政府计划对本乡镇道路进行改造，安排甲、乙两个工程队完成，已知甲工程队比乙工程队每天多改造20米，甲工程队改造200米的道路与乙工程队改造150米的道路所用时间相同，求甲、乙两个工程队每天改造的道路长度．

查看试题解析
19. 已知 $(2 x - 21) (3 x - 7) - (3 x - 7) (x - 13)$ 可分解因式为 $(3 x + a) (x + b)$ ，其中a ， b均为整数.

(1)、求 $a + 3 b$ 的值；

(2)、类似的，请你把 $x^{2} - 3 x + 2$ 分解成 $(x + a) (x + b)$ 的形式.

查看试题解析
20.

(1)、课本再现
已知：如图， $D E$ 是 $△ A B C$ 的中位线．求证： $D E ∥ B C$ ，且 $D E = \frac{1}{2} B C$ ．
定理证明
证明：如图1，延长 $D E$ 至点 $F$ ，使得 $E F = D E$ ，连接 $C F$ ．请你根据小乐添加的辅助线，写出完整的证明过程；（不再添加新的辅助线）

(2)、知识应用
如图2，在四边形 $A B C D$ 中， $A B = 6$ ， $C D = 8$ ， $∠ B A C = 30 °$ ， $∠ A C D = 120 °$ ，点 $E$ ， $F$ ， $M$ 分别是 $A D$ ， $B C$ ， $A C$ 的中点，求 $E F$ 的长．

查看试题解析
21. 如图，在△ABC中，∠CAB的平分线AD与BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC的延长线于N.

(1)、求证：BM=CN；

(2)、若AB=8，AC=4，求BM的长.

查看试题解析
22. 为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买 $2$ 个甲种文具、 $1$ 个乙种文具共需花费 $35$ 元；购买 $1$ 个甲种文具、 $3$ 个乙种文具共需花费 $30$ 元．

(1)、求购买一个甲种文具、一个乙种文具各需多少元？

(2)、若学校计划购买这两种文具共 $120$ 个，投入资金不少于 $955$ 元又不多于 $1000$ 元，设购买甲种文具 $x$ 个，求有多少种购买方案？

(3)、设学校投入资金 $W$ 元，在（2）的条件下，哪种购买方案需要的资金最少？最少资金是多少元？

查看试题解析
23. 旋转是一种重要的图形变换，当图形中有一组邻边相等时往往可以通过旋转解决问题．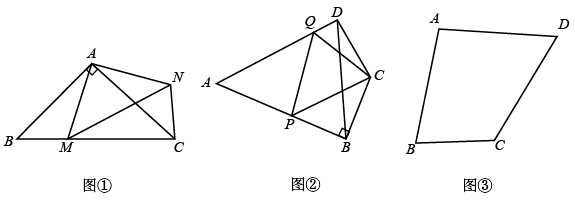

(1)、尝试解决：如图①，在等腰 $R t △ A B C$ 中， $∠ B A C = 90 ° ， A B = A C$ ，点M是 $B C$ 上的一点， $B M = 1 cm$ ， $C M = 2 cm$ ，将 $△ A B M$ 绕点A旋转后得到 $△ A C N$ ，连接 $M N$ ，则 $A M =$ $cm$ ．

(2)、类比探究：如图②，在“筝形”四边形 $A B C D$ 中， $A B = A D = a ， C B = C D ， A B ⊥ B C$ 于点B ， $A D ⊥ C D$ 于点D ，点P、Q分别是 $A B 、 A D$ 上的点，且 $∠ P C B + ∠ Q C D = ∠ P C Q$ ，求 $△ A P Q$ 的周长．（结果用a表示）

(3)、拓展应用：如图③，已知四边形 $A B C D$ ， $A D = C D ， ∠ A D C = 60 ° ， ∠ A B C = 75 ° ， A B = 2 \sqrt{2} ， B C = 2$ ，求四边形 $A B C D$ 的面积．

查看试题解析